Illustrative Math Alignment: Grade 6 Unit 9

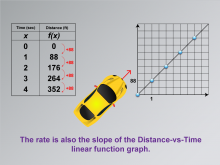
Topic

Quadratics

Description

This image presents a table with time in seconds and distance in feet, accompanied by a graph illustrating a linear relationship between time and distance. The constant increase of 88 feet per second is depicted as the slope of the Distance-vs-Time linear function graph. This visual aids students in understanding how linear functions can model real-world speed scenarios.

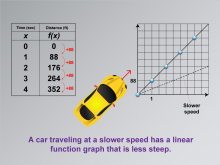
Topic

Quadratics

Description

This image is a variation showing time and distance data with a graph that includes a dotted line labeled "Slower speed." The graph illustrates how different speeds affect the steepness of linear function graphs. This visual comparison helps students see how speed variations are represented mathematically.

Using math clip art allows students to visualize differences in speed through graphical representations, aiding comprehension of linear functions' applications.

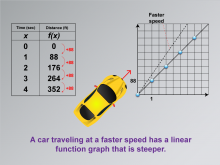
Topic

Quadratics

Description

This image shows a graph similar to the previous one but with a steeper dotted line labeled "Faster speed." It visually demonstrates how increased speed results in a steeper slope on a linear function graph. This helps students understand the relationship between speed changes and their graphical representations.

The use of math clip art facilitates learning by providing clear visual examples that connect mathematical concepts to real-world scenarios.

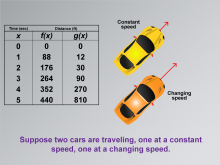
Topic

Quadratics

Description

This image displays a table with time and distance data for two functions, f(x) representing constant speed, and g(x) representing changing speed. Two car icons illustrate these concepts visually. This comparison allows students to explore how different types of motion are modeled mathematically.

The use of math clip art aids in understanding complex concepts by providing relatable visual examples that highlight differences in mathematical functions.

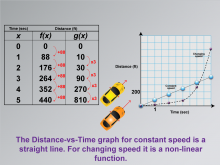
Topic

Quadratics

Description

This image presents time-distance data for functions f(x) with constant increments, showing constant speed, while g(x) shows changing speed with a common ratio. The visual representation helps students understand different mathematical relationships through real-world examples.

The use of math clip art enhances comprehension by clearly illustrating abstract concepts like common differences versus common ratios in mathematical functions.

Topic

Quadratics

Description

This image features a graph comparing linear and non-linear functions, illustrating constant and changing speeds. The visual contrast between the two types of functions helps students understand how different speeds are modeled mathematically. The linear function represents constant speed, while the non-linear function shows acceleration or deceleration.

Math clip art like this is crucial for teaching because it provides visual clarity, helping students differentiate between linear and quadratic functions in real-world contexts.

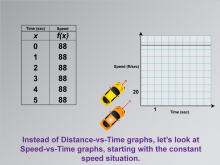
Topic

Quadratics

Description

This image illustrates a constant speed through a graph that shows a straight line, representing uniform motion. It provides an opportunity for students to see how consistent motion is represented visually in a linear function. The consistent slope indicates constant speed, making it easier for students to connect mathematical concepts with practical applications.

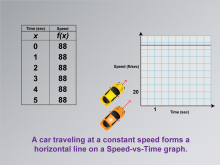
Topic

Quadratics

Description

This image shows a graph and data for a constant speed scenario. The graph helps students understand how different speeds are represented in mathematical models, with linear sections indicating constant speed and curved sections showing acceleration or deceleration.

Math clip art like this is essential for teaching as it visually differentiates between linear and quadratic functions, providing clarity in understanding real-world applications.

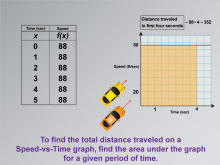
Topic

Quadratics

Description

This image includes a Speed-vs-Time graph with an area under the curve highlighted to represent distance traveled over time. The calculation for distance (88 * 4 = 352) is shown, helping students visualize how to determine total distance using graphs.

The use of math clip art enhances learning by providing visual context for abstract concepts like integration in real-world scenarios.

Teacher's Script: "See the shaded area? It represents distance. How do we calculate it? Let's find out."

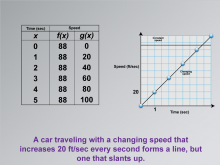
Topic

Quadratics

Description

This image shows a graph displaying two lines: a horizontal line for constant speed and a slanted line for changing speed. It illustrates how different speeds are represented graphically, helping students understand the concept of acceleration.

The use of math clip art provides clarity by visually differentiating between constant and changing speeds, aiding comprehension.

Teacher's Script: "Look at these lines. How do they show different speeds? Let's explore what these shapes tell us."

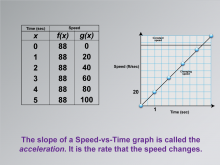
Topic

Quadratics

Description

This image includes a table with time (x) and speed (f(x) and g(x)). The graph shows constant and changing speeds, emphasizing the slope. The slope of a Speed-vs-Time graph is called acceleration, which is the rate that speed changes.

The use of math clip art helps students visualize how acceleration is represented graphically, aiding in understanding real-world applications.

Teacher's Script: "Notice the slope of these lines. How does it show acceleration? Let's explore what this means for speed changes."

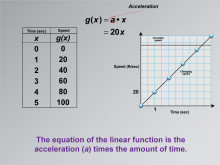
Topic

Quadratics

Description

This image presents a table with time (x) and speed (g(x)). The graph emphasizes acceleration as the slope, with an equation showing g(x) = 20x. The equation of the linear function is the acceleration (a) times the amount of time.

The use of math clip art clarifies how equations relate to real-world motion, enhancing comprehension.

Teacher's Script: "See how the equation shows acceleration? What does the slope tell us about speed changes?"

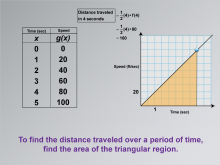
Topic

Quadratics

Description

This image features a table with time versus speed data, along with a graph that explains finding distance by calculating the area under a triangular region. To find the distance traveled over a period, calculate the area of the triangular region.

The use of math clip art aids in understanding by connecting theoretical concepts with practical applications.

Teacher's Script: "Notice how we find distance using the triangle area. How does this connect to what we've learned about motion?"

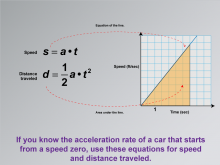
Topic

Quadratics

Description

This image displays a graph with speed versus time, highlighting the equation of the line and the area under it. It emphasizes using these equations when acceleration starts from zero. If you know the acceleration rate of a car that starts from speed zero, use these equations for speed and distance traveled.

The use of math clip art provides visual clarity in understanding how equations model motion from rest.

Teacher's Script: "Notice these equations—how do they help us understand acceleration from rest?"

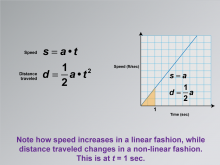
Topic

Quadratics

Description

This image shows a graph with speed on the y-axis and time on the x-axis. The equations for speed and distance traveled are given as s = a⋅t and d = 1/2at2. The graph illustrates how speed increases linearly, while distance traveled follows a non-linear path.

Math clip art like this helps students understand the difference between linear and quadratic relationships in real-world contexts.

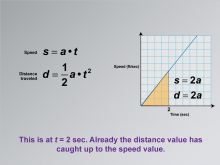
Topic

Quadratics

Description

This image shows a graph similar to the previous image but at t = 2 seconds. The equations are updated to s = 2a and d = 2a, indicating that distance has caught up with speed.

The use of math clip art provides visual clarity in understanding dynamic interactions between speed and distance over time.

Teacher's Script: "At two seconds, notice how distance catches up to speed. What does this mean for our understanding of motion?"

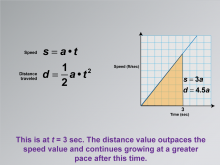
Topic

Quadratics

Description

This image depicts a graph of speed versus time with no initial velocity. The equations shown are s = a⋅t for speed and d = 1/2at2 for distance traveled. At t = 3 seconds, the graph highlights that distance outpaces speed.

The use of math clip art helps students visualize how distance can grow faster than speed under certain conditions.

Teacher's Script: "At three seconds, see how distance outpaces speed? Let's explore why this happens."

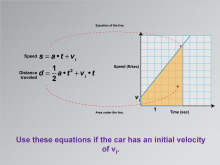
Topic

Quadratics

Description

This image shows a graph with a line representing speed as a function of time, with initial velocity. The equations for speed are s = a⋅t+vi ​ and for distance traveled are d= 1/2at2 +vi ​•t. The graph illustrates the area under the line, indicating distance.

The use of math clip art provides students with visual tools to understand how initial velocity affects motion over time.

Teacher's Script: "Notice how initial velocity changes the graph. How does this affect our calculations for distance?"

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Subtraction isn't commutative.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Subtraction isn't commutative.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division.

Because addition is commutative, adding from left to right, or right to left, gives you the same result.

The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations.

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

This is part of a collection of math clip art images that focus on the order of operations.

To see the complete collection of images on this topic, click on this link.

Watch the following video on Order of Operations. (The transcript is included.)

Video Transcript

Topic

Exponents

Description

Shows Example 1 with the expression 32. The solution explains how to simplify by multiplying 3 by itself according to the exponent. Example 1: Simplify 32. Multiply 3 by itself two times: 3•3 = 9.

Topic

Exponents

Description

Shows Example 2 with the expression 43. The solution explains the simplification by multiplying 4 three times. Example 2: Simplify 43. Multiply 4 by itself three times: 4•4•4 = 64.

In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents.

Topic

Exponents

Description

Shows Example 3 with the expression 54. The solution details multiplying 5 four times. Example 3: Simplify 54. Multiply 5 by itself four times: 5•5•5•5 = 625.

In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents.

Topic

Exponents

Description

Shows Example 4 with the expression 106. The solution simplifies by multiplying 10 six times. Example 4: Simplify 106. Multiply 10 by itself six times: 10•10•10•10•10•10 = 1,000,000.