
Illustrative Math Alignment: Grade 7 Unit 3
Measuring Circles
Lesson 5: Circumference and Wheels
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
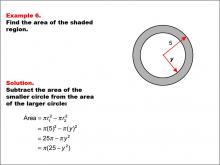
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |
|
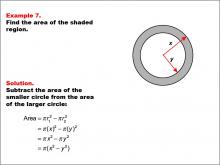
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |
|
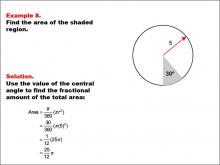
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |
|
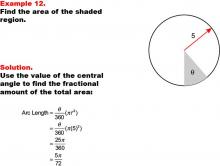
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |
|
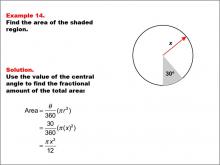
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |
| Applications of Linear Functions: Circumference vs. Diameter | Description
As the size of a circle changes, so does the size of the diameter and that of the circumference. In fact, there is a linear relationship between these two measures. This relationship can be modeled with a linear function. In this module students will study this linear function and examine its properties, including the fact that the slope of this function is π itself. This is a hands-on module in which students will measure the diameters and circumferences of a number of different containers. This data gathering will lead to graphing the data. From that students develop a linear model using the Desmos graphing tool. Students will see that the relationship between circumference and diameter has to do with π. In fact, the slope of the linear function is π itself. |
Applications of Ratios, Proportions, and Percents and Applications of Circles | |
| Circular Structures | Description
In this lesson students will use their basic understanding of circles to learn how circular structures are built. The example shown is that of the Roman Colosseum. Students will construct an oval shape from circular arcs to simulate the elliptical shape of the Roman Colosseum. For this lesson make sure that students have ready access to a compass, ruler, grid paper (graph paper with x-y axes marked is preferred), and pencil with an eraser. The first construction has students creating a teardrop shape from circular arcs that have overlapping points of tangency. This first construction sets up the more elaborate second construction. |
Applications of Circles |