
Illustrative Math Alignment: Grade 7 Unit 4
Proportional Relationships and Percentages
Lesson 15: Error Intervals
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Clip Art--Ratios, Proportions, Percents--Percents 07 | Math Clip Art--Ratios, Proportions, Percents--Percents 07TopicRatios, Proportions, and Percents DescriptionThe image illustrates percentages as fractions with a denominator of 100, such as 10% = 10 / 100, 15% = 15 / 100, and so on. It expands on this idea by showing how percents relate to fractions, reinforcing their equivalency and further grounding the concept. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |
|
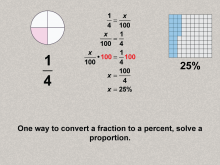
Math Clip Art--Ratios, Proportions, Percents--Percents 08 | Math Clip Art--Ratios, Proportions, Percents--Percents 08TopicRatios, Proportions, and Percents DescriptionThe image illustrates how to convert 1/4 to a percent using the proportion method: (1 / 4 = x / 100), solving for x = 25%. and expands on this idea by showing that provides a step-by-step method to convert fractions to percents, introducing proportional reasoning. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |
|
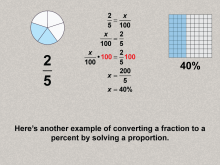
Math Clip Art--Ratios, Proportions, Percents--Percents 09 | Math Clip Art--Ratios, Proportions, Percents--Percents 09TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of converting a fraction to a percent using proportions, with 2/5 converting to 40%. and expands on this idea by showing that reinforces the proportion method with another example, building understanding through repetition. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 10 | Math Clip Art--Ratios, Proportions, Percents--Percents 10TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of converting fractions to percents, dividing 5 by 8 to get 62.5% and expands on this idea by showing an alternative method for conversion, allowing for flexibility in approaches. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |
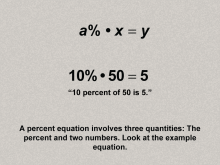
|
Math Clip Art--Ratios, Proportions, Percents--Percents 11 | Math Clip Art--Ratios, Proportions, Percents--Percents 11TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of the general equation for percents: a% * x = y, using the example 10% * 50 = 5. It emphasizes the three components of a percent equation: the percent, a base number, and the result, and expands on this idea by showing that establishes the foundational equation for solving percent problems, serving as a gateway to explore specific types of percent equations. |
Percents |
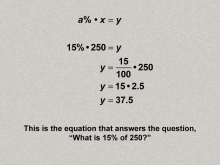
|
Math Clip Art--Ratios, Proportions, Percents--Percents 12 | Math Clip Art--Ratios, Proportions, Percents--Percents 12TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of how to solve the question 'what is 15% of 250?' using the equation a% * x = y, with calculations explicitly shown as 15 * 2.5 = 37.5. and expands on this idea by showing that provides a clear, step-by-step example to apply the general percent equation, enhancing comprehension through practical application. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 13 | Math Clip Art--Ratios, Proportions, Percents--Percents 13TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of solving '150 is 30% of what number?' using the same equation a% * x = y and algebraic manipulation to find x = 500 and expands on this idea by showing that explains how to rearrange the percent equation to solve for different variables, expanding on problem-solving strategies. |
Percents |
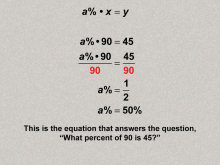
|
Math Clip Art--Ratios, Proportions, Percents--Percents 14 | Math Clip Art--Ratios, Proportions, Percents--Percents 14TopicRatios, Proportions, and Percents DescriptionThe image illustrates solving the problem 'what percent of 90 is 45?' using the equation a% * x = y, and algebraically finding a% = 50% and expands on this idea by showing that demonstrates how to find the percent in percent equations, further developing flexibility in solving percent-related problems. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 15 | Math Clip Art--Ratios, Proportions, Percents--Percents 15TopicRatios, Proportions, and Percents DescriptionThe image summarizes the three types of percent equations in a table format, highlighting the unknown variable in each scenario (percent, part, or whole) and expands on this idea by providing a comprehensive overview and categorization of percent problems, solidifying the framework introduced in earlier examples. |
Percents |
|
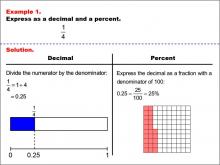
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 1 | Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 1TopicFractions |
Relate Fractions to Decimals |
|
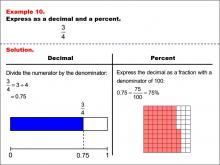
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 10 | Fractions, Decimals, and Percents: Example 10TopicFractions |
Relate Fractions to Decimals |
|
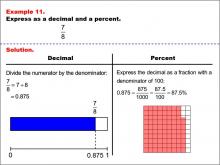
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 11 | Fractions, Decimals, and Percents: Example 11TopicFractions |
Relate Fractions to Decimals |
|
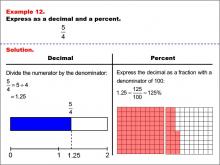
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 12 | Fractions, Decimals, and Percents: Example 12TopicFractions |
Relate Fractions to Decimals |
|
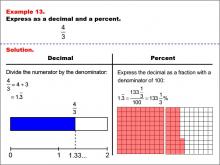
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 13 | Fractions, Decimals, and Percents: Example 13TopicFractions |
Relate Fractions to Decimals |
|
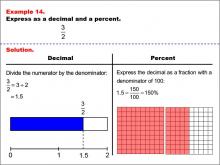
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 14 | Fractions, Decimals, and Percents: Example 14TopicFractions |
Relate Fractions to Decimals |
|
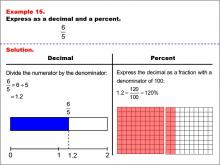
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 15 | Fractions, Decimals, and Percents: Example 15TopicFractions |
Relate Fractions to Decimals |
|
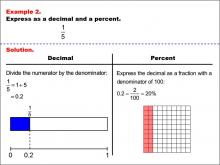
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 2 | Fractions, Decimals, and Percents: Example 2TopicFractions |
Relate Fractions to Decimals |
|
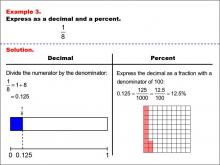
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 3 | Fractions, Decimals, and Percents: Example 3TopicFractions |
Relate Fractions to Decimals |
|
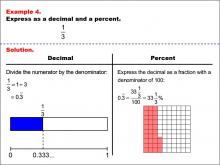
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 4 | Fractions, Decimals, and Percents: Example 4TopicFractions |
Relate Fractions to Decimals |
|
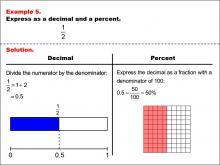
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 5 | Fractions, Decimals, and Percents: Example 5TopicFractions |
Relate Fractions to Decimals |
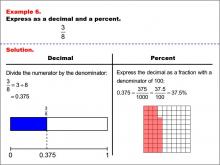
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 6 | Fractions, Decimals, and Percents: Example 6TopicFractions |
Relate Fractions to Decimals |
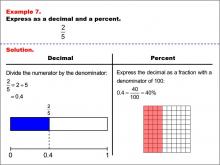
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 7 | Fractions, Decimals, and Percents: Example 7TopicFractions |
Relate Fractions to Decimals |
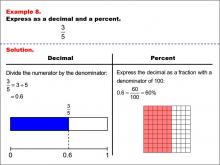
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 8 | Fractions, Decimals, and Percents: Example 8TopicFractions |
Relate Fractions to Decimals |
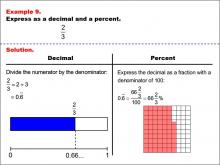
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 9 | Fractions, Decimals, and Percents: Example 9TopicFractions |
Relate Fractions to Decimals |

|
Math Example--Percents--Equations with Percents: Example 1 | Math Example--Percents--Equations with Percents: Example 1TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 5% of 8?" The solution involves converting 5% to its decimal form, 0.05, and then multiplying it by 8 to get the result of 0.4. This straightforward approach demonstrates how to tackle basic percent calculations efficiently. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 10 | Math Example--Percents--Equations with Percents: Example 10TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 170% of 9.5?" The solution involves converting 170% to its decimal equivalent, 1.7, and then multiplying it by 9.5 to obtain the result of 16.15. This example combines a percentage greater than 100% with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 11 | Math Example--Percents--Equations with Percents: Example 11TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 225.5% of 78?" The solution involves converting 225.5% to its decimal form, 2.255, and then multiplying it by 78 to arrive at the answer of 175.89. This example introduces a decimal percentage greater than 200% and a larger whole number as the base value, demonstrating the scalability and flexibility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 12 | Math Example--Percents--Equations with Percents: Example 12TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 400% of 92.8?" The solution involves converting 400% to its decimal equivalent, 4.0, and then multiplying it by 92.8 to obtain the result of 371.2. This example showcases how to handle percentages greater than 100% and their application to decimal numbers, illustrating the versatility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 13 | Math Example--Percents--Equations with Percents: Example 13TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "5 is what percent of 9?" The solution involves setting up the equation 9 * (x / 100) = 5, then solving for x to get x = 5 * (100 / 9), which is approximately 55.56%. This example introduces a new type of percent problem where students must find the percentage given two known values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 14 | Math Example--Percents--Equations with Percents: Example 14TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "6 is what percent of 2.3?" The solution involves setting up the equation 2.3 * (x / 100) = 6, then solving for x to get x = 6 * (100 / 2.3), which is approximately 260.87%. This example introduces a scenario where the resulting percentage is greater than 100% and involves a decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 15 | Math Example--Percents--Equations with Percents: Example 15TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is what percent of 38?" The solution involves setting up the equation 38 * (x / 100) = 9, then solving for x to get x = 9 * (100 / 38), which is approximately 23.68%. This example demonstrates how to calculate a percentage when the first number is smaller than the second, resulting in a percentage less than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 16 | Math Example--Percents--Equations with Percents: Example 16TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "2 is what percent of 55.5?" The solution involves setting up the equation 55.5 * (x / 100) = 2, then solving for x to get x = 2 * (100 / 55.5), which is approximately 3.6036%. This example introduces a scenario where the resulting percentage is a small fraction, less than 5%, and involves a decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 17 | Math Example--Percents--Equations with Percents: Example 17TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "8 is what percent of 120?" The solution involves setting up the equation 120 * (x / 100) = 8, then solving for x to get x = 8 * (100 / 120), which is approximately 6.67%. This example demonstrates how to calculate a percentage when dealing with larger whole numbers, resulting in a percentage less than 10%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 18 | Math Example--Percents--Equations with Percents: Example 18TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "3.5 is what percent of 350?" The solution involves setting up the equation 350 * (x / 100) = 3.5, then solving for x to get x = 3.5 * (100 / 350), which equals 1%. This example introduces a scenario where the resulting percentage is a whole number (1%) and involves a decimal number as the first value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 19 | Math Example--Percents--Equations with Percents: Example 19TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "12 is what percent of 8?" The solution involves setting up the equation 8 * (x / 100) = 12, then solving for x to get x = 12 * (100 / 8), which equals 150%. This example demonstrates how to calculate a percentage when the first number is larger than the second, resulting in a percentage greater than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 2 | Math Example--Percents--Equations with Percents: Example 2TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 7% of 9.5?" The solution involves converting 7% to its decimal equivalent, 0.07, and then multiplying it by 9.5 to obtain the result of 0.665. This example builds upon the previous one by introducing a decimal number as the base value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 20 | Math Example--Percents--Equations with Percents: Example 20TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "32 is what percent of 1.5?" The solution involves setting up the equation 1.5 * (x / 100) = 32, then solving for x to get x = 32 * (100 / 1.5), which equals 2133.3%. This example introduces a scenario where the resulting percentage is significantly larger than 100% and involves a decimal base number less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 21 | Math Example--Percents--Equations with Percents: Example 21TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "48 is what percent of 55?" The solution involves setting up the equation 55 * (x / 100) = 48, then solving for x to get x = 48 * (100 / 55), which equals 87.27%. This example demonstrates how to calculate a percentage when the two numbers are relatively close in value, resulting in a percentage close to but less than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 22 | Math Example--Percents--Equations with Percents: Example 22TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "52.2 is what percent of 98.5?" The solution involves setting up the equation 98.5 * (x / 100) = 52.2, then solving for x to get x = 52.2 * (100 / 98.5), which is approximately 52.99%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that is also close to the original numerator. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 23 | Math Example--Percents--Equations with Percents: Example 23TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "68 is what percent of 320?" The solution involves setting up the equation 320 * (x / 100) = 68, then solving for x to get x = 68 * (100 / 320), which equals 21.25%. This example demonstrates how to calculate a percentage when dealing with whole numbers, resulting in a percentage that's less than 25%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 24 | Math Example--Percents--Equations with Percents: Example 24TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "75.5 is what percent of 555.25?" The solution involves setting up the equation 555.25 * (x / 100) = 75.5, then solving for x to get x = 75.5 * (100 / 555.25), which is approximately 13.59%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that's less than 15%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 25 | Math Example--Percents--Equations with Percents: Example 25TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "125 is what percent of 2?" The solution involves setting up the equation 2 * (x / 100) = 125, then solving for x to get x = 125 * (100 / 2), which equals 6250%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage well over 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 26 | Math Example--Percents--Equations with Percents: Example 26TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 3.5?" The solution involves setting up the equation 3.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 3.5), which equals 8571.43%. This example introduces a scenario where the resulting percentage is extremely large, over 8000%, due to the first number being significantly larger than the small decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 27 | Math Example--Percents--Equations with Percents: Example 27TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "278 is what percent of 99?" The solution involves setting up the equation 99 * (x / 100) = 278, then solving for x to get x = 278 * (100 / 99), which equals 280.80%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage greater than 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 28 | Math Example--Percents--Equations with Percents: Example 28TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 75.5?" The solution involves setting up the equation 75.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 75.5), which equals 397.35%. This example introduces a scenario where the resulting percentage is close to 400%, with the first number being significantly larger than the decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 29 | Math Example--Percents--Equations with Percents: Example 29TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is what percent of 220?" The solution involves setting up the equation 220 * (x / 100) = 400, then solving for x to get x = 400 * (100 / 220), which equals 181.81%. This example demonstrates how to calculate a percentage when the first number is nearly double the second, resulting in a percentage between 150% and 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 3 | Math Example--Percents--Equations with Percents: Example 3TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 8% of 58?" The solution involves converting 8% to its decimal form, 0.08, and then multiplying it by 58 to arrive at the answer of 4.64. This example introduces a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 30 | Math Example--Percents--Equations with Percents: Example 30TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "333.5 is what percent of 500.25?" The solution involves setting up the equation 500.25 * (x / 100) = 333.5, then solving for x to get x = 333.5 * (100 / 500.25), which is approximately 66.67%. This example introduces a scenario where both numbers are decimals and the resulting percentage is less than 100%, showing how to handle more complex decimal calculations. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 31 | Math Example--Percents--Equations with Percents: Example 31TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "4 is 0.1% of what number?" The solution involves setting up the equation 4 = 0.001 * x, then solving for x to get x = 4 / 0.001, which equals 4000. This example demonstrates how to calculate the whole when given a very small percentage of it, resulting in a much larger number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 32 | Math Example--Percents--Equations with Percents: Example 32TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "7 is 1% of what number?" The solution involves setting up the equation 7 = 0.01 * x, then solving for x to get x = 7 / 0.01, which equals 700. This example introduces a scenario where we need to find the whole when given a small percentage of it, resulting in a number 100 times larger than the given value. |
Solving Percent Equations |