
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 6: Fermi Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Clip Art--Ratios, Proportions, Percents--Percents 07 | Math Clip Art--Ratios, Proportions, Percents--Percents 07TopicRatios, Proportions, and Percents DescriptionThe image illustrates percentages as fractions with a denominator of 100, such as 10% = 10 / 100, 15% = 15 / 100, and so on. It expands on this idea by showing how percents relate to fractions, reinforcing their equivalency and further grounding the concept. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |
|
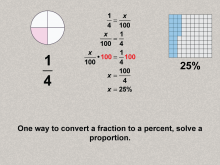
Math Clip Art--Ratios, Proportions, Percents--Percents 08 | Math Clip Art--Ratios, Proportions, Percents--Percents 08TopicRatios, Proportions, and Percents DescriptionThe image illustrates how to convert 1/4 to a percent using the proportion method: (1 / 4 = x / 100), solving for x = 25%. and expands on this idea by showing that provides a step-by-step method to convert fractions to percents, introducing proportional reasoning. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |
|
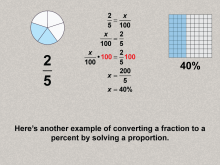
Math Clip Art--Ratios, Proportions, Percents--Percents 09 | Math Clip Art--Ratios, Proportions, Percents--Percents 09TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of converting a fraction to a percent using proportions, with 2/5 converting to 40%. and expands on this idea by showing that reinforces the proportion method with another example, building understanding through repetition. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 10 | Math Clip Art--Ratios, Proportions, Percents--Percents 10TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of converting fractions to percents, dividing 5 by 8 to get 62.5% and expands on this idea by showing an alternative method for conversion, allowing for flexibility in approaches. The topic of Ratios, Proportions, and Percents explores fundamental math concepts by using practical examples. This collection aids in visualizing the connection between different mathematical forms such as ratios, percents, and fractions, making abstract concepts more accessible to students. |
Percents |
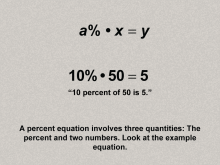
|
Math Clip Art--Ratios, Proportions, Percents--Percents 11 | Math Clip Art--Ratios, Proportions, Percents--Percents 11TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of the general equation for percents: a% * x = y, using the example 10% * 50 = 5. It emphasizes the three components of a percent equation: the percent, a base number, and the result, and expands on this idea by showing that establishes the foundational equation for solving percent problems, serving as a gateway to explore specific types of percent equations. |
Percents |
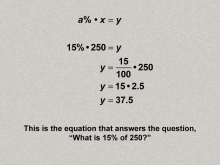
|
Math Clip Art--Ratios, Proportions, Percents--Percents 12 | Math Clip Art--Ratios, Proportions, Percents--Percents 12TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of how to solve the question 'what is 15% of 250?' using the equation a% * x = y, with calculations explicitly shown as 15 * 2.5 = 37.5. and expands on this idea by showing that provides a clear, step-by-step example to apply the general percent equation, enhancing comprehension through practical application. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 13 | Math Clip Art--Ratios, Proportions, Percents--Percents 13TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of solving '150 is 30% of what number?' using the same equation a% * x = y and algebraic manipulation to find x = 500 and expands on this idea by showing that explains how to rearrange the percent equation to solve for different variables, expanding on problem-solving strategies. |
Percents |
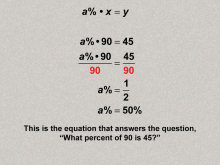
|
Math Clip Art--Ratios, Proportions, Percents--Percents 14 | Math Clip Art--Ratios, Proportions, Percents--Percents 14TopicRatios, Proportions, and Percents DescriptionThe image illustrates solving the problem 'what percent of 90 is 45?' using the equation a% * x = y, and algebraically finding a% = 50% and expands on this idea by showing that demonstrates how to find the percent in percent equations, further developing flexibility in solving percent-related problems. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 15 | Math Clip Art--Ratios, Proportions, Percents--Percents 15TopicRatios, Proportions, and Percents DescriptionThe image summarizes the three types of percent equations in a table format, highlighting the unknown variable in each scenario (percent, part, or whole) and expands on this idea by providing a comprehensive overview and categorization of percent problems, solidifying the framework introduced in earlier examples. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
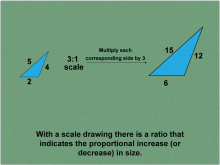
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
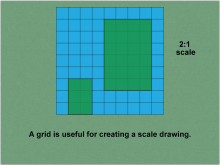
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
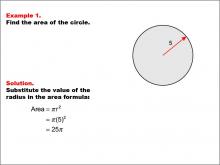
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 1TopicGeometry DescriptionThis example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 1TopicGeometry DescriptionThis example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 1TopicGeometry DescriptionThis example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |
|
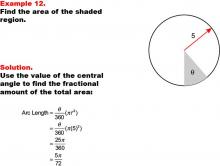
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |
|
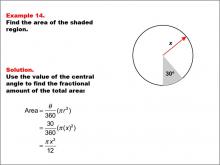
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 15TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 15TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 15TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π. |
Area and Circumference |
|
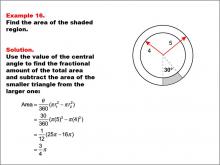
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |
|
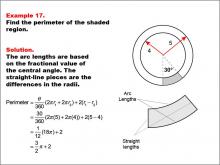
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 17TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 17TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 17TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 18TopicGeometry DescriptionThis example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 18TopicGeometry DescriptionThis example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 18TopicGeometry DescriptionThis example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2). |
Area and Circumference |
|
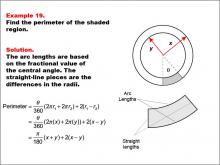
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 19TopicGeometry DescriptionThis example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 19TopicGeometry DescriptionThis example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 19TopicGeometry DescriptionThis example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 2 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 2TopicGeometry DescriptionThis example features a circle with a radius of 5 units. The objective is to calculate the circumference of the circle using the given radius. The solution involves applying the circumference formula: C = 2 * π * r = 2 * π * (5) = 10π. Circular area and circumference calculations are fundamental in geometry. These examples provide students with practical applications of theoretical concepts, helping them understand the relationship between a circle's radius and its circumference. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 2 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 2TopicGeometry DescriptionThis example features a circle with a radius of 5 units. The objective is to calculate the circumference of the circle using the given radius. The solution involves applying the circumference formula: C = 2 * π * r = 2 * π * (5) = 10π. Circular area and circumference calculations are fundamental in geometry. These examples provide students with practical applications of theoretical concepts, helping them understand the relationship between a circle's radius and its circumference. |
Area and Circumference |