
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 6: Fermi Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
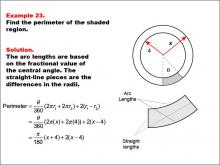
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 23TopicGeometry DescriptionThis example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 23TopicGeometry DescriptionThis example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 3TopicGeometry DescriptionThis example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 3TopicGeometry DescriptionThis example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 3TopicGeometry DescriptionThis example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 4TopicGeometry DescriptionThis example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 4TopicGeometry DescriptionThis example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 4TopicGeometry DescriptionThis example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference. |
Area and Circumference |
|
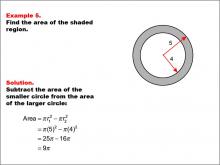
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 5TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 5TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 5TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes. |
Area and Circumference |
|
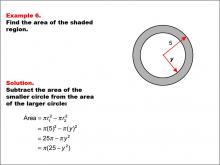
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |
|
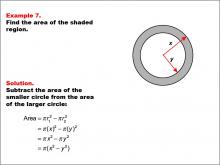
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |
|
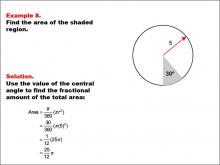
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |

|
Math Example--Math of Money--Calculating Tax--Example 1 | Math Example--Math of Money--Calculating Tax--Example 1TopicThe Math of Money DescriptionWhat is the tax due on a $1000 purchase when the sales tax rate is 5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 1 | Math Example--Math of Money--Calculating Tax--Example 1TopicThe Math of Money DescriptionWhat is the tax due on a $1000 purchase when the sales tax rate is 5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 1 | Math Example--Math of Money--Calculating Tax--Example 1TopicThe Math of Money DescriptionWhat is the tax due on a $1000 purchase when the sales tax rate is 5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 1 | Math Example--Math of Money--Calculating Tax--Example 1TopicThe Math of Money DescriptionWhat is the tax due on a $1000 purchase when the sales tax rate is 5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 10 | Math Example--Math of Money--Calculating Tax--Example 10TopicThe Math of Money DescriptionWhat is the tax due on a $9999.99 purchase when the sales tax rate is 9.9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 10 | Math Example--Math of Money--Calculating Tax--Example 10TopicThe Math of Money DescriptionWhat is the tax due on a $9999.99 purchase when the sales tax rate is 9.9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 10 | Math Example--Math of Money--Calculating Tax--Example 10TopicThe Math of Money DescriptionWhat is the tax due on a $9999.99 purchase when the sales tax rate is 9.9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 10 | Math Example--Math of Money--Calculating Tax--Example 10TopicThe Math of Money DescriptionWhat is the tax due on a $9999.99 purchase when the sales tax rate is 9.9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 2 | Math Example--Math of Money--Calculating Tax--Example 2TopicThe Math of Money DescriptionWhat is the tax due on a $1500 purchase when the sales tax rate is 6%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 2 | Math Example--Math of Money--Calculating Tax--Example 2TopicThe Math of Money DescriptionWhat is the tax due on a $1500 purchase when the sales tax rate is 6%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 2 | Math Example--Math of Money--Calculating Tax--Example 2TopicThe Math of Money DescriptionWhat is the tax due on a $1500 purchase when the sales tax rate is 6%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 2 | Math Example--Math of Money--Calculating Tax--Example 2TopicThe Math of Money DescriptionWhat is the tax due on a $1500 purchase when the sales tax rate is 6%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 3 | Math Example--Math of Money--Calculating Tax--Example 3TopicThe Math of Money DescriptionWhat is the tax due on a $2550 purchase when the sales tax rate is 7%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 3 | Math Example--Math of Money--Calculating Tax--Example 3TopicThe Math of Money DescriptionWhat is the tax due on a $2550 purchase when the sales tax rate is 7%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 3 | Math Example--Math of Money--Calculating Tax--Example 3TopicThe Math of Money DescriptionWhat is the tax due on a $2550 purchase when the sales tax rate is 7%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 3 | Math Example--Math of Money--Calculating Tax--Example 3TopicThe Math of Money DescriptionWhat is the tax due on a $2550 purchase when the sales tax rate is 7%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 4 | Math Example--Math of Money--Calculating Tax--Example 4TopicThe Math of Money DescriptionWhat is the tax due on a $999 purchase when the sales tax rate is 8%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 4 | Math Example--Math of Money--Calculating Tax--Example 4TopicThe Math of Money DescriptionWhat is the tax due on a $999 purchase when the sales tax rate is 8%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 4 | Math Example--Math of Money--Calculating Tax--Example 4TopicThe Math of Money DescriptionWhat is the tax due on a $999 purchase when the sales tax rate is 8%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 4 | Math Example--Math of Money--Calculating Tax--Example 4TopicThe Math of Money DescriptionWhat is the tax due on a $999 purchase when the sales tax rate is 8%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 5 | Math Example--Math of Money--Calculating Tax--Example 5TopicThe Math of Money DescriptionWhat is the tax due on a $999.99 purchase when the sales tax rate is 9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 5 | Math Example--Math of Money--Calculating Tax--Example 5TopicThe Math of Money DescriptionWhat is the tax due on a $999.99 purchase when the sales tax rate is 9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 5 | Math Example--Math of Money--Calculating Tax--Example 5TopicThe Math of Money DescriptionWhat is the tax due on a $999.99 purchase when the sales tax rate is 9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 5 | Math Example--Math of Money--Calculating Tax--Example 5TopicThe Math of Money DescriptionWhat is the tax due on a $999.99 purchase when the sales tax rate is 9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 6 | Math Example--Math of Money--Calculating Tax--Example 6TopicThe Math of Money DescriptionWhat is the tax due on a $1250 purchase when the sales tax rate is 6.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 6 | Math Example--Math of Money--Calculating Tax--Example 6TopicThe Math of Money DescriptionWhat is the tax due on a $1250 purchase when the sales tax rate is 6.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 6 | Math Example--Math of Money--Calculating Tax--Example 6TopicThe Math of Money DescriptionWhat is the tax due on a $1250 purchase when the sales tax rate is 6.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |