
Illustrative Math Alignment: Grade 8 Unit 1
Rigid Transformations and Congruence
Lesson 12: Congruent Polygons
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Clip Art--Geometry Concepts--Kite Shape 6 | Math Clip Art--Kite Shape 6TopicGeometry Concepts DescriptionThis image illustrates a hexagonal kite shape. Geometrically, a kite is a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. Teacher's Script: "Observe this kite. How is it a kite in the everyday sense? Is it a kite in the geometric sense?" |
Definition of a Polygon and Definition of a Triangle |

|
Math Clip Art--Geometry Concepts--Kite Shape 7 | Math Clip Art--Kite Shape 7TopicGeometry Concepts DescriptionThis image features a kite shape, a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. |
Definition of a Polygon and Definition of a Triangle |
|
Math Clip Art--Geometry Concepts--Kite Shape 8 | Math Clip Art--Kite Shape 8TopicGeometry Concepts DescriptionThis image depicts a kite shape, characterized by two pairs of adjacent equal-length sides and diagonals that intersect at right angles. This geometric configuration is symmetrical and unique. Kite shapes are used to explore geometric properties such as symmetry, area, and perimeter. They are applicable in various fields, including mathematics, design, and architecture. Teacher's Script: "Look at this kite shape. How do its symmetrical properties and intersecting diagonals help us understand its geometry? What are some mathematical concepts you can explore using kite shapes?" |
Definition of a Polygon and Definition of a Triangle |

|
Math Clip Art--Geometry Concepts--Kite Shape 9 | Math Clip Art--Kite Shape 9TopicGeometry Concepts DescriptionThis image illustrates a kite shape, a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. |
Definition of a Polygon and Definition of a Triangle |
|
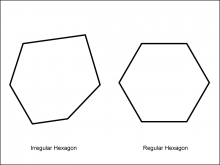
Math Clip Art--Geometry Concepts--Polygons--Hexagon | Math Clip Art--Polygons--HexagonTopicGeometry Concepts DescriptionThis image illustrates two hexagons: one regular and one irregular. A hexagon is a six-sided polygon. In a regular hexagon, all sides and angles are equal, with each interior angle measuring 120 degrees. This symmetry gives it a balanced and uniform appearance. An irregular hexagon, by contrast, has sides and angles that are not all equal. This lack of uniformity means that the hexagon can take on a variety of shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
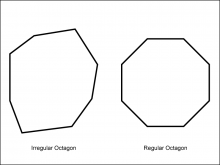
Math Clip Art--Geometry Concepts--Polygons--Octagon | Math Clip Art--Polygons--OctagonTopicGeometry Concepts DescriptionThis image shows two octagons: one regular and one irregular. An octagon is an eight-sided polygon. In a regular octagon, all sides and angles are equal, with each interior angle measuring 135 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular octagon, on the other hand, has sides and angles that are not all equal. This asymmetry means that the octagon can have a variety of shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
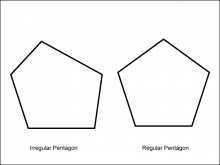
Math Clip Art--Geometry Concepts--Polygons--Pentagon | Math Clip Art--Polygons--PentagonTopicGeometry Concepts DescriptionThis image depicts two pentagons: one regular and one irregular. A pentagon is a five-sided polygon. In a regular pentagon, all sides and angles are equal, with each interior angle measuring 108 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular pentagon, however, has sides and angles that are not all equal. This asymmetry allows the pentagon to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
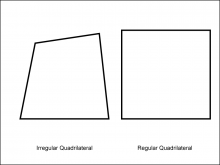
Math Clip Art--Geometry Concepts--Polygons--Quadrilateral | Math Clip Art--Polygons--QuadrilateralTopicGeometry Concepts DescriptionThis image illustrates two quadrilaterals: one regular and one irregular. A quadrilateral is a four-sided polygon. In a regular quadrilateral, such as a square, all sides and angles are equal, with each interior angle measuring 90 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular quadrilateral, however, has sides and angles that are not all equal. This asymmetry allows the quadrilateral to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
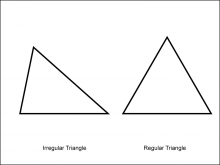
Math Clip Art--Geometry Concepts--Polygons--Triangle | Math Clip Art--Polygons--TriangleTopicGeometry Concepts DescriptionThis image shows two triangles: one regular and one irregular. A triangle is a three-sided polygon. In a regular triangle, also known as an equilateral triangle, all sides and angles are equal, with each interior angle measuring 60 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular triangle, however, has sides and angles that are not all equal. This asymmetry allows the triangle to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
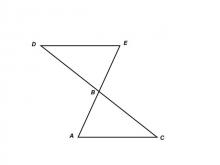
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
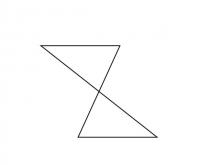
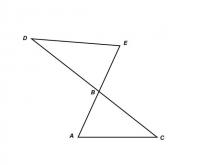
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
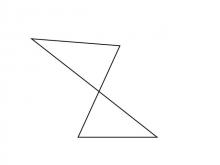
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
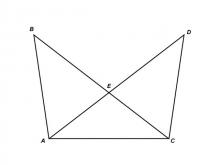
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
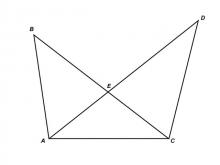
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
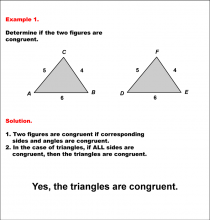
|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF also has sides 5, 4, and 6. The SSS Postulate ensures that these triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
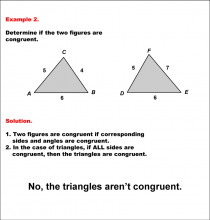
|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF has sides 5, 7, and 6. Because corresponding sides are not all congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
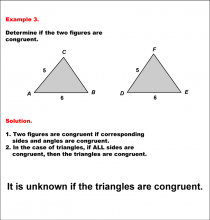
|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6, and triangle DEF has sides 5 and 6, but no information on the third side. As a result, there isn't enough information to know if they are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have two sides (5 and 6) and an included angle of 60°. As a results of the SAS Postulate, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6 with an included angle of 60°, and triangle DEF has sides 5 and 6 with an included angle of 62°. Because corresponding angles are not congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have angles of 63°, 60°, and 57°, but no information on side lengths. As a result, we can't conclude if the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. Both triangles appear identical in shape and orientation, positioned differently on the grid. Using the grid, you can see that corresponding sides are congruent. Therefore the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
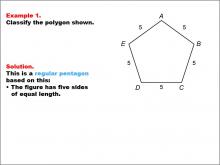
|
Math Example--Polygons--Polygon Classification: Example 1 | Math Example--Polygons--Polygon Classification: Example 1TopicPolygons DescriptionThis example showcases a pentagon with all sides labeled as 5. It demonstrates a regular pentagon, characterized by five sides of equal length. This visual representation helps students understand the concept of regular polygons and their defining characteristics. The topic of polygon classification is crucial in geometry. This collection of examples provides a comprehensive look at various types of pentagons, both regular and irregular. By examining different configurations of sides and angles, students can develop a deeper understanding of polygon properties and classification criteria. |
Definition of a Polygon |
|
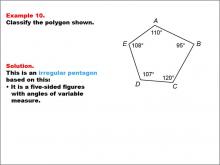
Math Example--Polygons--Polygon Classification: Example 10 | Math Example--Polygons--Polygon Classification: Example 10TopicPolygons DescriptionThis example showcases a pentagon labeled with vertices A, B, C, D, E, where the angles are marked as 110°, 95°, 120°, 107°, and 108°. It demonstrates an irregular pentagon based on the variation in angle measures, highlighting that regularity depends on both side lengths and angle measures. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples emphasizes the importance of both side lengths and angle measures in determining the regularity of pentagons. |
Definition of a Polygon |
|
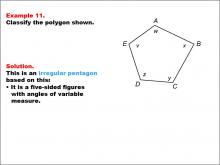
Math Example--Polygons--Polygon Classification: Example 11 | Math Example--Polygons--Polygon Classification: Example 11TopicPolygons DescriptionThis example presents a pentagon labeled with vertices A, B, C, D, E, where the sides are marked with variables w, x, y, z, and v. It illustrates an irregular pentagon by using different variables to represent potentially different side lengths, emphasizing that side length variation results in irregularity. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various types of pentagons, highlighting the importance of side length equality in determining regularity. |
Definition of a Polygon |
|
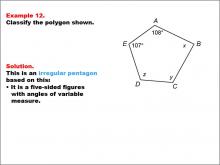
Math Example--Polygons--Polygon Classification: Example 12 | Math Example--Polygons--Polygon Classification: Example 12TopicPolygons DescriptionThis example features a pentagon labeled with vertices A, B, C, D, E, where the angles are marked as 108°, x, y, z, and 107°. It demonstrates an irregular pentagon based on the variation in angle measures, highlighting that regularity depends on all angles being equal. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples emphasizes the importance of angle measures in determining the regularity of pentagons, showing that even one different angle makes the polygon irregular. |
Definition of a Polygon |
|
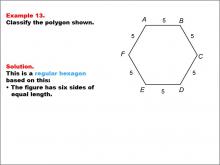
Math Example--Polygons--Polygon Classification: Example 13 | Math Example--Polygons--Polygon Classification: Example 13TopicPolygons DescriptionThis example showcases a hexagon with all sides labeled as 5, indicating equal length. It demonstrates a regular hexagon, characterized by six sides of equal length. This visual representation helps students understand the concept of regular polygons and their defining characteristics. The topic of polygon classification is crucial in geometry. This collection of examples provides a comprehensive look at various types of hexagons, both regular and irregular. By examining different configurations of sides and angles, students can develop a deeper understanding of polygon properties and classification criteria. |
Definition of a Polygon |
|
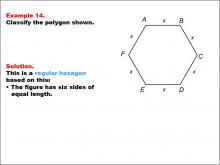
Math Example--Polygons--Polygon Classification: Example 14 | Math Example--Polygons--Polygon Classification: Example 14TopicPolygons DescriptionThis example presents a hexagon with all sides labeled as x, indicating equal length. It illustrates another instance of a regular hexagon, reinforcing the concept that a regular polygon has all sides of equal length, even when represented by a variable. Polygon classification is a fundamental topic in geometry that helps students understand the properties and characteristics of different shapes. This collection of examples provides a comprehensive overview of various hexagon types, allowing students to distinguish between regular and irregular polygons based on their side lengths and angle measures. |
Definition of a Polygon |
|
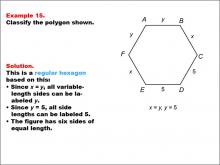
Math Example--Polygons--Polygon Classification: Example 15 | Math Example--Polygons--Polygon Classification: Example 15TopicPolygons DescriptionThis example features a hexagon with sides labeled y, x, and 5, showing that x = y = 5, making all sides equal in length. It demonstrates a regular hexagon by using a combination of variables and numeric values to represent equal side lengths. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights different ways to represent regular hexagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
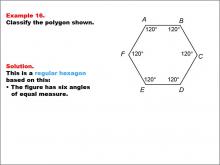
Math Example--Polygons--Polygon Classification: Example 16 | Math Example--Polygons--Polygon Classification: Example 16TopicPolygons DescriptionThis example showcases a hexagon with all interior angles labeled as 120 degrees, indicating equal angles. It demonstrates that a regular hexagon can be identified not only by equal side lengths but also by equal angle measures, reinforcing the dual criteria for regularity in polygons. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various aspects of regular hexagons, emphasizing both side length and angle measure as defining characteristics. |
Definition of a Polygon |
|
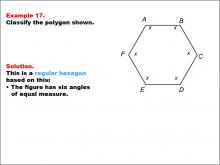
Math Example--Polygons--Polygon Classification: Example 17 | Math Example--Polygons--Polygon Classification: Example 17TopicPolygons DescriptionThis example presents a hexagon with six equal sides labeled as x and equal angles, indicating a regular hexagon. It reinforces the concept of a regular polygon by visually representing both the equality of all sides and angles. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples provides various representations of regular hexagons, emphasizing the importance of both side length and angle measure equality in classification. |
Definition of a Polygon |
|
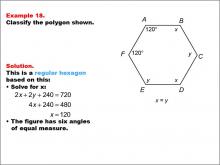
Math Example--Polygons--Polygon Classification: Example 18 | Math Example--Polygons--Polygon Classification: Example 18TopicPolygons DescriptionThis example features a hexagon with two angles labeled as 120 degrees and sides labeled x and y, where x = y. It demonstrates how to determine if a hexagon is regular by solving for the unknown angle measures and confirming equal side lengths. Polygon classification is a crucial topic in geometry that helps students distinguish between regular and irregular shapes. This collection of examples provides a comprehensive look at various types of hexagons, highlighting the importance of both angle measures and side lengths in determining regularity. |
Definition of a Polygon |
|
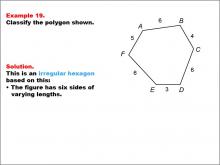
Math Example--Polygons--Polygon Classification: Example 19 | Math Example--Polygons--Polygon Classification: Example 19TopicPolygons DescriptionThis example showcases a hexagon with sides labeled with varying lengths: AB = 6, BC = 4, CD = 6, DE = 3, EF = 6, and FA = 5. It demonstrates an irregular hexagon, emphasizing that side length variation results in irregularity. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights the differences between regular and irregular hexagons, focusing on side length as a key determining factor. |
Definition of a Polygon |
|
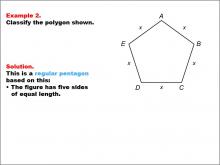
Math Example--Polygons--Polygon Classification: Example 2 | Math Example--Polygons--Polygon Classification: Example 2TopicPolygons DescriptionThis example presents a pentagon with all sides labeled as x, indicating equal length. It illustrates another instance of a regular pentagon, reinforcing the concept that a regular polygon has all sides of equal length. Polygon classification is a fundamental topic in geometry that helps students understand the properties and characteristics of different shapes. This collection of examples provides a comprehensive overview of various pentagon types, allowing students to distinguish between regular and irregular polygons based on their side lengths and angle measures. |
Definition of a Polygon |
|
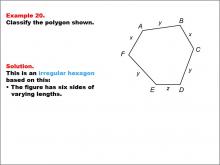
Math Example--Polygons--Polygon Classification: Example 20 | Math Example--Polygons--Polygon Classification: Example 20TopicPolygons DescriptionThis example presents a hexagon with sides labeled as x, y, and z, indicating varying lengths. It illustrates another case of an irregular hexagon, demonstrating that the presence of different variables for side lengths suggests irregularity. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various types of hexagons, emphasizing the importance of side length equality in determining regularity. |
Definition of a Polygon |
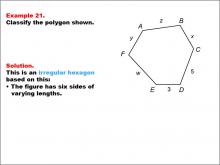
|
Math Example--Polygons--Polygon Classification: Example 21 | Math Example--Polygons--Polygon Classification: Example 21
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
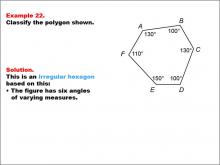
|
Math Example--Polygons--Polygon Classification: Example 22 | Math Example--Polygons--Polygon Classification: Example 22
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
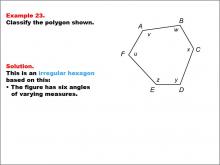
|
Math Example--Polygons--Polygon Classification: Example 23 | Math Example--Polygons--Polygon Classification: Example 23
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
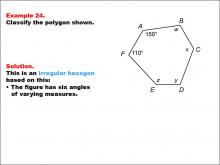
|
Math Example--Polygons--Polygon Classification: Example 24 | Math Example--Polygons--Polygon Classification: Example 24
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
|
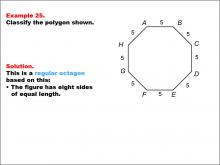
Math Example--Polygons--Polygon Classification: Example 25 | Math Example--Polygons--Polygon Classification: Example 25TopicPolygons DescriptionThis example showcases an octagon with all sides labeled as 5, indicating equal length. It demonstrates a regular octagon, characterized by eight sides of equal length. This visual representation helps students understand the concept of regular polygons and their defining characteristics. The topic of polygon classification is crucial in geometry. This collection of examples provides a comprehensive look at various types of octagons, both regular and irregular. By examining different configurations of sides and angles, students can develop a deeper understanding of polygon properties and classification criteria. |
Definition of a Polygon |
|
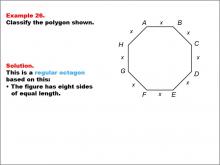
Math Example--Polygons--Polygon Classification: Example 26 | Math Example--Polygons--Polygon Classification: Example 26TopicPolygons DescriptionThis example presents an octagon with all sides labeled as x, indicating equal length. It illustrates another instance of a regular octagon, reinforcing the concept that a regular polygon has all sides of equal length, even when represented by a variable. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples provides various representations of regular octagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
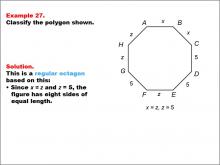
Math Example--Polygons--Polygon Classification: Example 27 | Math Example--Polygons--Polygon Classification: Example 27TopicPolygons DescriptionThis example features an octagon with sides labeled as x, z, and 5, showing that x = z = 5, indicating equal length for all sides. It demonstrates a regular octagon by using a combination of variables and numeric values to represent equal side lengths. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various aspects of regular octagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
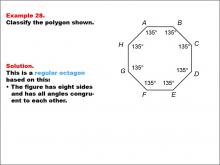
Math Example--Polygons--Polygon Classification: Example 28 | Math Example--Polygons--Polygon Classification: Example 28TopicPolygons DescriptionThis example showcases an octagon with all angles labeled as 135 degrees, indicating congruent angles. It demonstrates that a regular octagon can be identified not only by equal side lengths but also by equal angle measures, reinforcing the dual criteria for regularity in polygons. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights different aspects of regular octagons, emphasizing both side length and angle measure as defining characteristics. |
Definition of a Polygon |
|
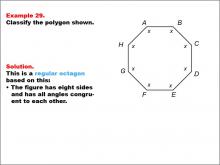
Math Example--Polygons--Polygon Classification: Example 29 | Math Example--Polygons--Polygon Classification: Example 29TopicPolygons DescriptionThis example presents an octagon with all angles labeled as "x," indicating a regular polygon. It illustrates a regular octagon by visually representing the equality of all angles using a single variable. This reinforces the concept that a regular polygon has all angles of equal measure. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various aspects of regular octagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
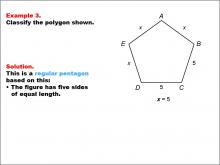
Math Example--Polygons--Polygon Classification: Example 3 | Math Example--Polygons--Polygon Classification: Example 3TopicPolygons DescriptionThis example features a pentagon with sides labeled x and two sides labeled as 5, with x = 5, demonstrating that all sides are equal. It reinforces the concept of a regular pentagon by showing how different notations can represent the same length. The study of polygon classification helps students develop critical thinking skills in geometry. This collection of examples illustrates various ways to represent and identify regular pentagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
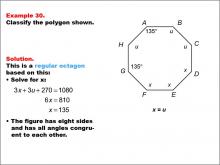
Math Example--Polygons--Polygon Classification: Example 30 | Math Example--Polygons--Polygon Classification: Example 30TopicPolygons DescriptionThis example features an octagon with angles labeled as 135° and angles labeled as "u" and "x." It demonstrates how to determine if an octagon is regular by solving for the unknown angle measures and confirming equal side lengths. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples provides insights into how partial information about angle measures and side lengths can be used to determine the regularity of octagons. |
Definition of a Polygon |