Illustrative Math Alignment: Grade 8 Unit 3

Functions and Volume

Lesson 1: Inputs and Outputs

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Quadratics Collection: Texas Instruments Graphing Calculator Resources	A set of resources for the TI-Nspire, TI-Nspire CX, and the Nspire App.	Applications of Quadratic Functions, Graphs of Quadratic Functions, Quadratic Formula, Data Analysis, Quadratic Equations and Functions, Inequalities and Composite Functions
Linear Functions and Equations Collection: Algebra Applications Videos	Real-world applications of linear functions and equations through this video series.	Special Functions and Applications of Linear Functions
Functions and Relations Collection: Basic Definitions	Here are key terms in the topic of Functions and Relations.	Relations and Functions and Conic Sections
Linear Functions and Equations Collection: Promethean Flipcharts	This is a collection of Promethean Flipcharts that focus on Linear Functions and Equations.	Applications of Linear Functions
Measures of Central Tendency: Basic Terms and Definitions	Here we gather key terms, definitions, and formulas around Measures of Central Tendency.	Data Analysis and Relations and Functions
Quadratics Collection: Instructional Resources	Here is a collection of PowerPoint presentations on selected topics in Quadratics.	Quadratic Equations and Functions, Applications of Quadratic Functions, Graphs of Quadratic Functions, Numerical and Algebraic Expressions and Quadratic Formula
Math Video Collection: Algebra Applications Video Series: Functions and Relations	Overview This collection aggregates all the math videos and resources in this series: Algebra Applications Video Series: Functions and Relations. There are a total of 26 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.	Applications of Functions and Relations, Conic Sections, Relations and Functions, Quadratic Equations and Functions and Geometric Constructions with Circles
Math Video Collection: Algebra Applications Video Series: Linear Functions	Overview This collection aggregates all the math videos and resources in this series: Algebra Applications Video Series: Linear Functions. There are a total of 26 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.	Special Functions, Applications of Linear Functions and Graphs of Linear Functions
Math Examples Collection: Function Rules	Overview This collection aggregates all the math examples around the topic of Function Rules. There are a total of 10 Math Examples. This collection of resources is made up of downloadable PNG images that you can easily incorporate into your lesson plans.	Relations and Functions
Math Definitions Collection: Functions and Relations	Overview The "Functions and Relations" collection from Media4Math provides a comprehensive set of definitions essential for understanding key mathematical concepts. This collection includes terms such as domain, range, function, relation, inverse function, and composite function. These definitions are crucial for students as they form the foundation for more advanced topics in mathematics, such as calculus and algebra.	Special Functions, Composite Functions, Conic Sections, Relations and Functions and Functions and Their Inverses
Math Games Collection: Drag-N-Drop	Overview This is a collection of all our drag-n-drop math games. There are a total of 34 games. These games cover a variety of different skills. Each comes with a large bank of questions, so each game experience will be different. These games are ideal for practice and review.	Addition Facts to 25, Counting, Subtraction Facts to 25, Place Value, Polynomial Expressions, Division Expressions and Equations, Point-Slope Form, Slope-Intercept Form, Standard Form, Slope, Applications of Linear Functions, Quadratic Equations and Functions, Data Analysis, Multiplication Expressions and Equations, Solving One-Step Equations, Quadratic Formula, Numerical Expressions, Variable Expressions and Solving Two-Step Equations
Quizlet Flash Card Collection: Evaluating Functions	Overview This is a collection of Quizlet Flash Cards on the topic of Evaluating Functions. There are a total of 56 Quizlet Flash Card sets. To see the complete collection of Quizlet Flash Cards, click on this link.	Applications of Linear Functions, Applications of Quadratic Functions, Applications of Exponential and Logarithmic Functions, Numerical Expressions and Relations and Functions
Interactive Media Collection: Linear Equations in Standards Form	Overview This collection aggregates all the math videos and other resources on the topic of Linear Equations in Standard Form. here are seven resources.	Standard Form
Algebra Applications Teacher's Guide: Functions and Relations	Algebra Applications Teacher's Guide: Functions and Relations This is the Teacher's Guide that accompanies Algebra Applications: Functions and Relations. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Functions and Relations
Algebra Applications Teacher's Guide: Linear Functions	Algebra Applications Teacher's Guide: Linear Functions This is the Teacher's Guide that accompanies Algebra Applications: Linear Functions. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Linear Functions
Algebra Applications Teacher's Guide: Quadratic Functions	Algebra Applications Teacher's Guide: Quadratic Functions This is the Teacher's Guide that accompanies Algebra Applications: Quadratic Functions. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Quadratic Functions
Algebra Applications: Dinosaur Footprints	Algebra Applications: Dinosaur Footprints Paleontologists rely on fossils to learn about dinosaurs. They also rely on certain algebraic concepts to help them estimate the sizes of dinosaurs based on the measurements of dinosaur footprints. In this activity, walk students through the solution of several proportions to estimate the sizes of different dinosaurs. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Proportions
Algebra Nspirations Teacher's Guide: Linear Functions	Algebra Nspirations Teacher's Guide: Linear Functions This is the Teacher's Guide that accompanies Algebra Nspirations: Linear Functions. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Linear Functions
Closed Captioned Video: Algebra Applications: Linear Functions, 1	Closed Captioned Video: Algebra Applications: Linear Functions, Segment 1: Introduction Linear Expressions, Equations, and Functions Linear Expres	Special Functions and Applications of Linear Functions
Closed Captioned Video: Algebra Applications: Linear Functions, 3	Closed Captioned Video: Algebra Applications: Linear Functions, Segment 3: Oil Exploration Linear Expressions, Equations, and Functions Linear Exp	Special Functions and Applications of Linear Functions
Closed Captioned Video: Algebra Nspirations: Functions and Relations	Closed Captioned Video: Algebra Nspirations: Functions and Relations Functions are relationships between quantities that change. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video explores the definition of a function, its vocabulary and notations, and distinguishes the concept of function from a general relation. Multiple representations of functions are provided using the TI-Nspire, while dynamic visuals and scenarios put them into real-world contexts. Concepts explored: functions, relations, equations, quadratic functions, linear functions, multiple representations.	Applications of Functions and Relations, Conic Sections and Relations and Functions
Definition--Functions and Relations Concepts--Absolute Value Function	Absolute Value Function Topic Functions and Relations Definition An absolute value function is a function that contains an algebraic expression within absolute value symbols. It is defined as $$ f(x) = \|x\| $$ where \|x\| denotes the absolute value ofx. Description The absolute value function is significant in mathematics because it measures the distance of a number from zero on the number line, regardless of direction. This function is linear in nature, as it can be broken into two linear pieces: one for $$ x \geq 0 $$ and one for $$ x < 0 $$	Special Functions
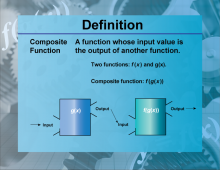
Definition--Functions and Relations Concepts--Composite Function	Composite Function Topic Functions and Relations Definition A composite function is a function that is formed when one function is applied to the result of another function. Description Composite functions are significant in mathematics because they allow the combination of two functions to form a new function. This is denoted as (f∘g)(x) = f(g(x)). Composite functions are widely used in various fields, including computer science for function composition in programming and in calculus for chain rule applications. For example, if f(x) = 2x and g(x) = x + 3, then the composite function (f∘g)(x) = f(g(x)) = 2(x + 3) = 2x+6	Composite Functions
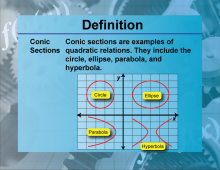
Definition--Functions and Relations Concepts--Conic Sections	Conic Sections Topic Functions and Relations Definition Conic sections are the curves obtained by intersecting a plane with a double-napped cone. Description Conic sections include circles, ellipses, parabolas, and hyperbolas, which are fundamental in the study of geometry and algebra. These shapes are described by quadratic equations and have numerous applications in physics, engineering, and astronomy. For example, the orbits of planets are ellipses, and parabolic mirrors are used in telescopes and satellite dishes. The general quadratic equation for conic sections is Ax2 + Bxy + Cy2 + Dx + Ey + F = 0	Conic Sections
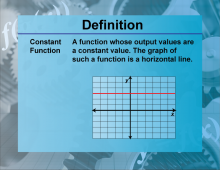
Definition--Functions and Relations Concepts--Constant Function	Constant Function Topic Functions and Relations Definition A constant function is a function that always returns the same value, no matter the input. Description The constant function is one of the simplest types of functions in mathematics, expressed as f(x) = c	Relations and Functions
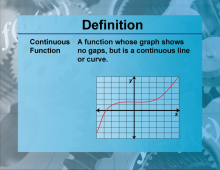
Definition--Functions and Relations Concepts--Continuous Function	Continuous Function Topic Functions and Relations Definition A continuous function is a function that does not have any breaks, holes, or gaps in its domain. Description Continuous functions are fundamental in calculus and mathematical analysis because they allow for the application of limits, derivatives, and integrals. A function f(x) is continuous if, for every point 𝑐 c in its domain, lim x→c f(x) = f(c)	Relations and Functions
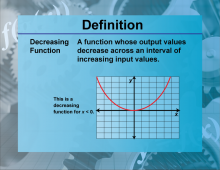
Definition--Functions and Relations Concepts--Decreasing Function	Decreasing Function Topic Functions and Relations Definition A decreasing function is a function where the value of the function decreases as the input increases. Description Decreasing functions are important in mathematics because they describe scenarios where an increase in one variable leads to a decrease in another. This is mathematically represented as f(x1) > f(x2) for any 𝑥1 < 𝑥2	Relations and Functions
Definition--Functions and Relations Concepts--Dependent Variable	Dependent Variable Topic Functions and Relations Definition A dependent variable is a variable whose value depends on one or more other variables.	Relations and Functions
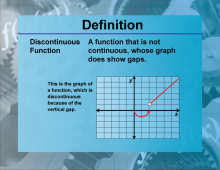
Definition--Functions and Relations Concepts--Discontinuous Function	Discontinuous Function Topic Functions and Relations Definition A discontinuous function is a function that has one or more points where it is not continuous.	Relations and Functions
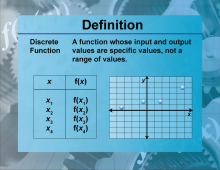
Definition--Functions and Relations Concepts--Discrete Functions	Discrete Functions Topic Functions and Relations Definition Discrete functions are functions that are defined only for a set of discrete points.	Special Functions
Definition--Functions and Relations Concepts--Distorting a Function Horizontally	Distorting a Function Horizontally Topic Functions and Relations Definition Distorting a function horizontally involves stretching or compressing the graph of the function along the x-axis. Description Horizontal distortions of functions are significant because they alter the input values while maintaining the overall shape of the graph. This is mathematically represented as f(kx) where k is a constant. If k > 1, the function compresses horizontally, and if 0 < 𝑘 < 1, it stretches.	Relations and Functions
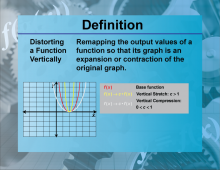
Definition--Functions and Relations Concepts--Distorting a Function Vertically	Distorting a Function Vertically Topic Functions and Relations Definition Distorting a function vertically involves stretching or compressing the graph of the function along the y-axis. Description Vertical distortions of functions are significant because they alter the output values while maintaining the overall shape of the graph. This is mathematically represented as kf(x)	Relations and Functions
Definition--Functions and Relations Concepts--Domain of a Function	Domain of a Function Topic Functions and Relations Definition The domain of a function is the set of all possible input values (x-values) for which the function is defined.	Relations and Functions
Definition--Functions and Relations Concepts--Even Function	Even Function Topic Functions and Relations Definition An even function is a function that satisfies the condition f(x) = f(−x) for all x in its domain. Description Even functions are important in mathematics because they exhibit symmetry about the y-axis. This property is useful in various fields, including physics and engineering, where symmetry simplifies analysis and problem-solving. For example, the function f(x)=x2	Relations and Functions
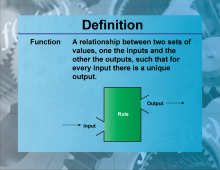
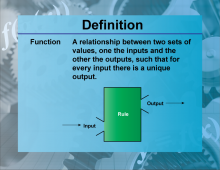
Definition--Functions and Relations Concepts--Function	Function Topic Functions and Relations Definition A function is a relation that uniquely associates each element of a set with exactly one element of another set.	Relations and Functions
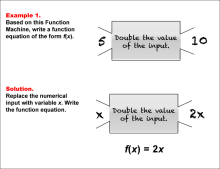
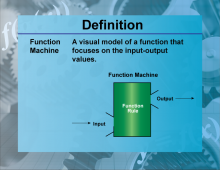
Definition--Functions and Relations Concepts--Function Machine	Function Machine Topic Functions and Relations Definition A function machine is a conceptual tool used to understand how functions work by visualizing inputs and outputs. Description The function machine is a useful educational tool that helps students grasp the concept of functions by visualizing the process of converting inputs into outputs. It emphasizes the idea that a function takes an input, processes it according to a specific rule, and produces an output. For example, if the function is f(x) = x + 2	Relations and Functions
Definition--Functions and Relations Concepts--Function Notation	Function Notation Topic Functions and Relations Definition Function notation is a way to represent functions in the form f(x), where f denotes the function and x denotes the input variable. Description Function notation is a standardized way to write functions, making it easier to understand and communicate mathematical relationships. It is widely used in algebra, calculus, and other branches of mathematics. For example, the notation f(x) = x2	Relations and Functions
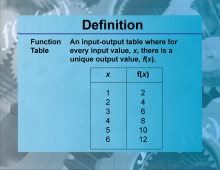
Definition--Functions and Relations Concepts--Function Table	Function Table Topic Functions and Relations Definition A function table is a table that lists input values and their corresponding output values for a given function. Description Function tables are useful tools in mathematics for organizing and analyzing the relationship between inputs and outputs of a function. They help in visualizing how a function behaves and in identifying patterns. For example, a function table for f(x) = 2x + 1	Relations and Functions
Definition--Functions and Relations Concepts--Graphs of Functions	Graphs of Functions Topic Functions and Relations Definition Graphs of functions are visual representations of the relationship between input values and output values of a function. Description Graphs of functions are essential tools in mathematics for visualizing how a function behaves. They provide a clear picture of the relationship between the input and output values, making it easier to analyze and interpret the function. For example, the graph of f(x) = x2	Relations and Functions
Definition--Functions and Relations Concepts--Graphs of Relations	Graphs of Relations Topic Functions and Relations Definition Graphs of relations are visual representations of the relationship between two sets of values, not necessarily functions.	Relations and Functions
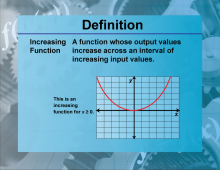
Definition--Functions and Relations Concepts--Increasing Function	Increasing Function Topic Functions and Relations Definition An increasing function is a function where the value of the function increases as the input increases.	Relations and Functions
Definition--Functions and Relations Concepts--Independent Variable	Independent Variable Topic Functions and Relations Definition An independent variable is a variable that represents the input or cause and is manipulated to observe its effect on the dependent variable.	Relations and Functions
Definition--Functions and Relations Concepts--Inverse Function	Inverse Function Topic Functions and Relations Definition An inverse function is a function that reverses the effect of the original function, such that f(f−1(x)) = x.	Functions and Their Inverses
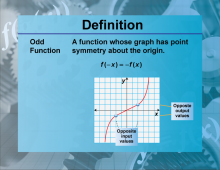
Definition--Functions and Relations Concepts--Odd Function	Odd Function Topic Functions and Relations Definition An odd function is a function that satisfies the condition f(−x) = −f(x) for all x in its domain.	Relations and Functions
Definition--Functions and Relations Concepts--Parametric Equations	Parametric Equations Topic Functions and Relations Definition Parametric equations are a set of equations that express the coordinates of the points of a curve as functions of a variable called a parameter.	Relations and Functions
Definition--Functions and Relations Concepts--Piecewise Functions	Piecewise Functions Topic Functions and Relations Definition Piecewise functions are functions defined by multiple sub-functions, each applying to a certain interval of the domain.	Special Functions
Definition--Functions and Relations Concepts--Range of a Function	Range of a Function Topic Functions and Relations Definition The range of a function is the set of all possible output values (y-values) that the function can produce. Description Understanding the range of a function is crucial in mathematics because it defines the scope of possible outputs. The range is determined by the function's rule and the domain. For example, the range of the function f(x) = x2	Relations and Functions
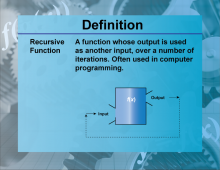
Definition--Functions and Relations Concepts--Recursive Function	Recursive Function Topic Functions and Relations Definition A recursive function is a function that calls itself in its definition. Description Recursive functions are important in mathematics and computer science because they provide a way to solve problems by breaking them down into simpler sub-problems. They are defined by a base case and a recursive case. For example, the factorial function f(n) = n⋅f(n−1) with f(0)=1	Relations and Functions
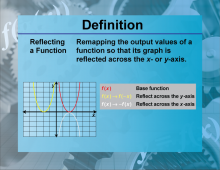
Definition--Functions and Relations Concepts--Reflecting a Function	Reflecting a Function Topic Functions and Relations Definition Reflecting a function involves flipping the graph of the function over a specified axis. Description Reflecting functions is significant in mathematics because it helps in understanding the symmetry and transformations of functions. A function can be reflected over the x-axis or y-axis, changing its orientation. For example, reflecting the function f(x) = x2	Relations and Functions
Definition--Functions and Relations Concepts--Relation	Relation Topic Functions and Relations Definition A relation is a set of ordered pairs, where each element from one set is paired with an element from another set.	Relations and Functions