
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 10: Piecewise Linear Functions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
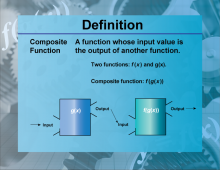
Definition--Functions and Relations Concepts--Composite Function | Composite FunctionTopicFunctions and Relations DefinitionA composite function is a function that is formed when one function is applied to the result of another function. DescriptionComposite functions are significant in mathematics because they allow the combination of two functions to form a new function. This is denoted as (f∘g)(x) = f(g(x)). Composite functions are widely used in various fields, including computer science for function composition in programming and in calculus for chain rule applications. For example, if f(x) = 2x and g(x) = x + 3, then the composite function (f∘g)(x) = f(g(x)) = 2(x + 3) = 2x+6 |
Composite Functions |
|
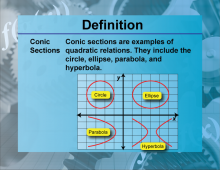
Definition--Functions and Relations Concepts--Conic Sections | Conic SectionsTopicFunctions and Relations DefinitionConic sections are the curves obtained by intersecting a plane with a double-napped cone. DescriptionConic sections include circles, ellipses, parabolas, and hyperbolas, which are fundamental in the study of geometry and algebra. These shapes are described by quadratic equations and have numerous applications in physics, engineering, and astronomy. For example, the orbits of planets are ellipses, and parabolic mirrors are used in telescopes and satellite dishes. The general quadratic equation for conic sections is Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 |
Conic Sections |
|
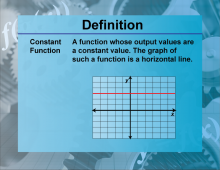
Definition--Functions and Relations Concepts--Constant Function | Constant FunctionTopicFunctions and Relations DefinitionA constant function is a function that always returns the same value, no matter the input. DescriptionThe constant function is one of the simplest types of functions in mathematics, expressed as f(x) = c |
Relations and Functions |
|
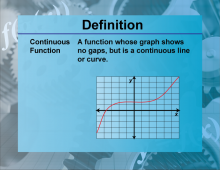
Definition--Functions and Relations Concepts--Continuous Function | Continuous FunctionTopicFunctions and Relations DefinitionA continuous function is a function that does not have any breaks, holes, or gaps in its domain. DescriptionContinuous functions are fundamental in calculus and mathematical analysis because they allow for the application of limits, derivatives, and integrals. A function f(x) is continuous if, for every point 𝑐 c in its domain, lim x→c f(x) = f(c) |
Relations and Functions |
|
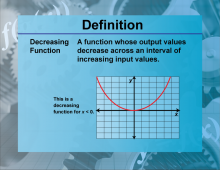
Definition--Functions and Relations Concepts--Decreasing Function | Decreasing FunctionTopicFunctions and Relations DefinitionA decreasing function is a function where the value of the function decreases as the input increases. DescriptionDecreasing functions are important in mathematics because they describe scenarios where an increase in one variable leads to a decrease in another. This is mathematically represented as f(x1) > f(x2) for any 𝑥1 < 𝑥2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Dependent Variable | Dependent VariableTopicFunctions and Relations DefinitionA dependent variable is a variable whose value depends on one or more other variables. |
Relations and Functions |
|
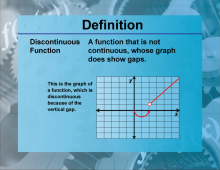
Definition--Functions and Relations Concepts--Discontinuous Function | Discontinuous FunctionTopicFunctions and Relations DefinitionA discontinuous function is a function that has one or more points where it is not continuous. |
Relations and Functions |
|
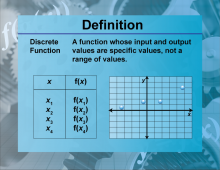
Definition--Functions and Relations Concepts--Discrete Functions | Discrete FunctionsTopicFunctions and Relations DefinitionDiscrete functions are functions that are defined only for a set of discrete points. |
Special Functions |

|
Definition--Functions and Relations Concepts--Distorting a Function Horizontally | Distorting a Function HorizontallyTopicFunctions and Relations DefinitionDistorting a function horizontally involves stretching or compressing the graph of the function along the x-axis. DescriptionHorizontal distortions of functions are significant because they alter the input values while maintaining the overall shape of the graph. This is mathematically represented as f(kx) where k is a constant. If k > 1, the function compresses horizontally, and if 0 < 𝑘 < 1, it stretches. |
Relations and Functions |
|
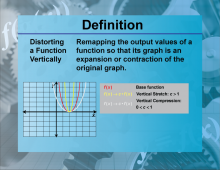
Definition--Functions and Relations Concepts--Distorting a Function Vertically | Distorting a Function VerticallyTopicFunctions and Relations DefinitionDistorting a function vertically involves stretching or compressing the graph of the function along the y-axis. DescriptionVertical distortions of functions are significant because they alter the output values while maintaining the overall shape of the graph. This is mathematically represented as kf(x) |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Domain of a Function | Domain of a FunctionTopicFunctions and Relations DefinitionThe domain of a function is the set of all possible input values (x-values) for which the function is defined. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Even Function | Even FunctionTopicFunctions and Relations DefinitionAn even function is a function that satisfies the condition f(x) = f(−x) for all x in its domain. DescriptionEven functions are important in mathematics because they exhibit symmetry about the y-axis. This property is useful in various fields, including physics and engineering, where symmetry simplifies analysis and problem-solving. For example, the function f(x)=x2 |
Relations and Functions |
|
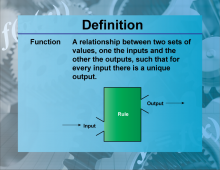
Definition--Functions and Relations Concepts--Function | FunctionTopicFunctions and Relations DefinitionA function is a relation that uniquely associates each element of a set with exactly one element of another set. |
Relations and Functions |
|
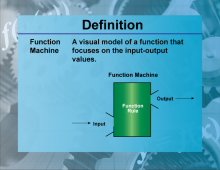
Definition--Functions and Relations Concepts--Function Machine | Function MachineTopicFunctions and Relations DefinitionA function machine is a conceptual tool used to understand how functions work by visualizing inputs and outputs. DescriptionThe function machine is a useful educational tool that helps students grasp the concept of functions by visualizing the process of converting inputs into outputs. It emphasizes the idea that a function takes an input, processes it according to a specific rule, and produces an output. For example, if the function is f(x) = x + 2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Function Notation | Function NotationTopicFunctions and Relations DefinitionFunction notation is a way to represent functions in the form f(x), where f denotes the function and x denotes the input variable. DescriptionFunction notation is a standardized way to write functions, making it easier to understand and communicate mathematical relationships. It is widely used in algebra, calculus, and other branches of mathematics. For example, the notation f(x) = x2 |
Relations and Functions |
|
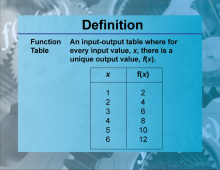
Definition--Functions and Relations Concepts--Function Table | Function TableTopicFunctions and Relations DefinitionA function table is a table that lists input values and their corresponding output values for a given function. DescriptionFunction tables are useful tools in mathematics for organizing and analyzing the relationship between inputs and outputs of a function. They help in visualizing how a function behaves and in identifying patterns. For example, a function table for f(x) = 2x + 1 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Graphs of Functions | Graphs of FunctionsTopicFunctions and Relations DefinitionGraphs of functions are visual representations of the relationship between input values and output values of a function. DescriptionGraphs of functions are essential tools in mathematics for visualizing how a function behaves. They provide a clear picture of the relationship between the input and output values, making it easier to analyze and interpret the function. For example, the graph of f(x) = x2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Graphs of Relations | Graphs of RelationsTopicFunctions and Relations DefinitionGraphs of relations are visual representations of the relationship between two sets of values, not necessarily functions. |
Relations and Functions |
|
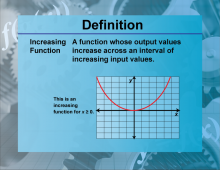
Definition--Functions and Relations Concepts--Increasing Function | Increasing FunctionTopicFunctions and Relations DefinitionAn increasing function is a function where the value of the function increases as the input increases. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Independent Variable | Independent VariableTopicFunctions and Relations DefinitionAn independent variable is a variable that represents the input or cause and is manipulated to observe its effect on the dependent variable. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Inverse Function | Inverse FunctionTopicFunctions and Relations DefinitionAn inverse function is a function that reverses the effect of the original function, such that f(f−1(x)) = x. |
Functions and Their Inverses |
|
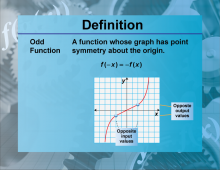
Definition--Functions and Relations Concepts--Odd Function | Odd FunctionTopicFunctions and Relations DefinitionAn odd function is a function that satisfies the condition f(−x) = −f(x) for all x in its domain. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Parametric Equations | Parametric EquationsTopicFunctions and Relations DefinitionParametric equations are a set of equations that express the coordinates of the points of a curve as functions of a variable called a parameter. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Piecewise Functions | Piecewise FunctionsTopicFunctions and Relations DefinitionPiecewise functions are functions defined by multiple sub-functions, each applying to a certain interval of the domain. |
Special Functions |

|
Definition--Functions and Relations Concepts--Range of a Function | Range of a FunctionTopicFunctions and Relations DefinitionThe range of a function is the set of all possible output values (y-values) that the function can produce. DescriptionUnderstanding the range of a function is crucial in mathematics because it defines the scope of possible outputs. The range is determined by the function's rule and the domain. For example, the range of the function f(x) = x2 |
Relations and Functions |
|
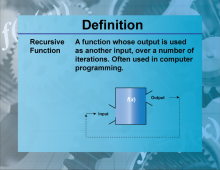
Definition--Functions and Relations Concepts--Recursive Function | Recursive FunctionTopicFunctions and Relations DefinitionA recursive function is a function that calls itself in its definition. DescriptionRecursive functions are important in mathematics and computer science because they provide a way to solve problems by breaking them down into simpler sub-problems. They are defined by a base case and a recursive case. For example, the factorial function f(n) = n⋅f(n−1) with f(0)=1 |
Relations and Functions |
|
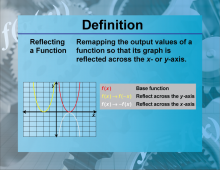
Definition--Functions and Relations Concepts--Reflecting a Function | Reflecting a FunctionTopicFunctions and Relations DefinitionReflecting a function involves flipping the graph of the function over a specified axis. DescriptionReflecting functions is significant in mathematics because it helps in understanding the symmetry and transformations of functions. A function can be reflected over the x-axis or y-axis, changing its orientation. For example, reflecting the function f(x) = x2 |
Relations and Functions |
|
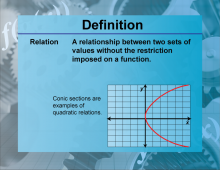
Definition--Functions and Relations Concepts--Relation | RelationTopicFunctions and Relations DefinitionA relation is a set of ordered pairs, where each element from one set is paired with an element from another set. |
Relations and Functions |
|
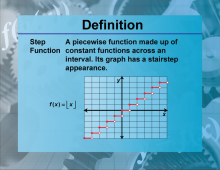
Definition--Functions and Relations Concepts--Step Function | Step FunctionTopicFunctions and Relations DefinitionA step function is a function that increases or decreases abruptly at certain points, creating a series of steps. |
Special Functions |
|
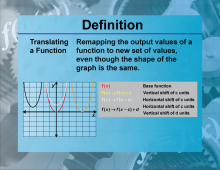
Definition--Functions and Relations Concepts--Translating a Function | Translating a FunctionTopicFunctions and Relations DefinitionTranslating a function involves shifting the graph of the function horizontally, vertically, or both, without changing its shape. DescriptionTranslating functions is significant in mathematics because it helps in understanding how functions behave under shifts. A function can be translated horizontally by adding or subtracting a constant to the input, and vertically by adding or subtracting a constant to the output. For example, translating the function f(x) = x2 horizontally by 2 units results in |
Relations and Functions |
|
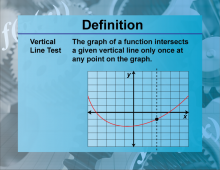
Definition--Functions and Relations Concepts--Vertical Line Test | Vertical Line TestTopicFunctions and Relations DefinitionThe vertical line test is a method used to determine if a graph represents a function by checking if any vertical line intersects the graph more than once. DescriptionThe vertical line test is important in mathematics because it helps in identifying whether a given graph represents a function. If a vertical line intersects the graph at more than one point, then the graph does not represent a function. This test is used in various fields, including computer science for validating functions in programming and in mathematics for analyzing graphs. For example, the graph of |
Relations and Functions |
|
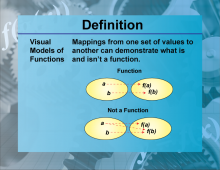
Definition--Functions and Relations Concepts--Visual Models of Functions | Visual Models of FunctionsTopicFunctions and Relations DefinitionVisual models of functions are graphical representations that illustrate the relationship between input and output values of functions. DescriptionVisual models of functions are important in mathematics because they provide a clear and intuitive way to understand how functions behave. These models include graphs, tables, and diagrams that show the relationship between input and output values. For example, the graph of f(x) = x2 |
Relations and Functions |
|
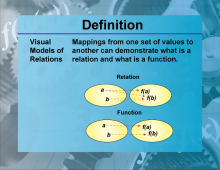
Definition--Functions and Relations Concepts--Visual Models of Relations | Visual Models of RelationsTopicFunctions and Relations DefinitionVisual models of relations are graphical representations that illustrate the relationship between two sets of values, not necessarily functions. |
Relations and Functions |
|
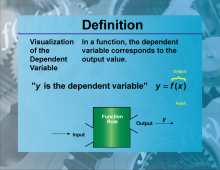
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable | Visualization of the Dependent VariableTopicFunctions and Relations DefinitionVisualization of the dependent variable involves graphically representing the outcomes or responses that depend on the independent variable. |
Relations and Functions |
|
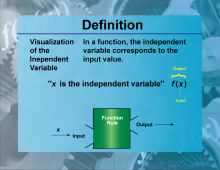
Definition--Functions and Relations Concepts--Visualization of the Independent Variable | Visualization of the Independent VariableTopicFunctions and Relations DefinitionVisualization of the independent variable involves graphically representing the variable that is manipulated to observe its effect on the dependent variable. |
Relations and Functions |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Accident Investigation | INSTRUCTIONAL RESOURCE: Algebra Application: Accident Investigation
In this Algebra Application, students develop a quadratic mathematical model for calculating the speed of a car based on the length of its skid marks. Using this model, students investigate the corresponding parabola. The math topics covered include: Mathematical modeling, Quadratic functions in standard form, Square root formula, Data analysis. The culminating activity is for students to write a program, using either a spreadsheet or a computer language like Python, that can calculate the speed of a car, given the skid mark length and coefficient of friction as the two inputs. |
Applications of Quadratic Functions and Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Creating an Exercise Chart | INSTRUCTIONAL RESOURCE: Algebra Application: Creating an Exercise Chart
In this Algebra Application, students develop a linear mathematical model based on the maximum heart rate during exercise based on age. Using this model, students investigate heart rate for moderate and vigorous workouts. The math topics covered include: Mathematical modeling, Linear functions, Families of functions, Computational thinking. The culminating activity is for students to create a simple program (using either a spreadsheet or a programming language like Python) to develop an exercise chart. This is a great back-to-school activity for middle school or high school students. A relevant real-world application allows them to review math concepts. |
Applications of Linear Functions and Slope-Intercept Form |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Fireworks Displays | INSTRUCTIONAL RESOURCE: Algebra Application: Fireworks Displays
In this Algebra Application, students develop a quadratic mathematical model based for the path of fireworks. Using this model, students investigate the properties of parabolas, including orientation, y-intercept, and vertex. The math topics covered include: Mathematical modeling, Quadratic functions in standard, vertex, and factored form, Curve fitting, Solving equations. The culminating activity is for students to plan a fireworks displays that mathematically uses the properties of quadratics restricted to the first quadrant. Given the coordinates of the vertices, what are the equations of parabolas that fit the given parameters. |
Applications of Quadratic Functions and Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter | INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter
In this Algebra Application, students study the direction between diameter and circumference of a circle. Through measurement and data gathering students analyze the line of best fit and explore ways of calculating pi. The math topics covered include: Mathematical modeling, Linear functions, Data gathering and analysis, Ratios, Direct variation. This is a great back-to-school activity for middle school or high school students. This is also a great crossover activity that ties algebra and geometry. |
Applications of Linear Functions, Applications of Ratios, Proportions, and Percents and Applications of Circles |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form
This slide show provides 8 examples of quadratic functions in factored form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Standard Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Standard Form
This slide show provides 18 examples of quadratic functions in standard form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Vertex Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Vertex Form
This slide show provides 8 examples of quadratic functions in vertex form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
Instructional Resource: Applications of Linear Functions: Circumference vs. Diameter | In this Slide Show, apply concepts of linear functions to the context of circumference vs. diameter. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Cost vs. Time | In this Slide Show, apply concepts of linear functions to the context of cost vs. time data and graphs. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Cricket Chirps | In this Slide Show, apply concepts of linear functions to the context of cricket chirps. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Distance vs. Time | In this Slide Show, apply concepts of linear functions to the context of distance vs. time data and graphs. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Hooke's Law | In this Slide Show, apply concepts of linear functions to the context of Hooke's law. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions and Proportions |

|
Instructional Resource: Applications of Linear Functions: Momentum and Impulse | In this Slide Show, apply concepts of linear functions to the context of momentum and impulse. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Perimeter of a Rectangle | In this Slide Show, apply concepts of linear functions to the context of rectangular perimeter. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Saving Money | In this Slide Show, apply concepts of linear functions to the context of saving money. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |