
Illustrative Math Alignment: Grade 8 Unit 6
Associations in Data
Lesson 1: Organizing Data
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
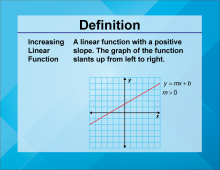
Definition--Linear Function Concepts--Increasing Linear Function | Increasing Linear Function
TopicLinear Functions DefinitionAn increasing linear function is a linear function where the slope is positive, indicating that as the input value increases, the output value also increases. DescriptionIncreasing linear functions are essential in understanding how variables positively relate to each other. The positive slope signifies an increase in the dependent variable as the independent variable increases. Real-world examples include income increasing with hours worked or the rise in temperature with the increase in daylight hours. These functions help model scenarios where an increase in one quantity results in an increase in another. |
Slope-Intercept Form |
|
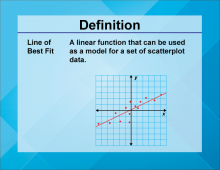
Definition--Linear Function Concepts--Line of Best Fit | Line of Best Fit
TopicLinear Functions DefinitionA line of best fit is a straight line that best represents the data on a scatter plot, showing the trend of the data points. DescriptionThe line of best fit is a crucial concept in statistics and data analysis. It helps in identifying the trend and making predictions based on the data. In real-world applications, the line of best fit is used in various fields such as economics, biology, and engineering to analyze trends and make forecasts. For example, it can be used to predict future sales based on past data. |
Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Line of Best Fit | Line of Best Fit
TopicLinear Functions DefinitionA line of best fit is a straight line that best represents the data on a scatter plot, showing the trend of the data points. DescriptionThe line of best fit is a crucial concept in statistics and data analysis. It helps in identifying the trend and making predictions based on the data. In real-world applications, the line of best fit is used in various fields such as economics, biology, and engineering to analyze trends and make forecasts. For example, it can be used to predict future sales based on past data. |
Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Line of Best Fit | Line of Best Fit
TopicLinear Functions DefinitionA line of best fit is a straight line that best represents the data on a scatter plot, showing the trend of the data points. DescriptionThe line of best fit is a crucial concept in statistics and data analysis. It helps in identifying the trend and making predictions based on the data. In real-world applications, the line of best fit is used in various fields such as economics, biology, and engineering to analyze trends and make forecasts. For example, it can be used to predict future sales based on past data. |
Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Linear Equations in Standard Form | Linear Equations in Standard Form
TopicLinear Functions DefinitionLinear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. DescriptionLinear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form. |
Standard Form |

|
Definition--Linear Function Concepts--Linear Equations in Standard Form | Linear Equations in Standard Form
TopicLinear Functions DefinitionLinear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. DescriptionLinear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form. |
Standard Form |

|
Definition--Linear Function Concepts--Linear Equations in Standard Form | Linear Equations in Standard Form
TopicLinear Functions DefinitionLinear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. DescriptionLinear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form. |
Standard Form |
|
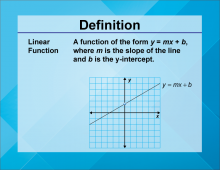
Definition--Linear Function Concepts--Linear Function | Linear Function
TopicLinear Functions DefinitionA linear function is a function that can be graphed as a straight line, typically written in the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionLinear functions are one of the most fundamental concepts in mathematics. They describe relationships where the rate of change between variables is constant, represented graphically as a straight line. This simplicity makes them a central topic in algebra and calculus. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Linear Function | Linear Function
TopicLinear Functions DefinitionA linear function is a function that can be graphed as a straight line, typically written in the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionLinear functions are one of the most fundamental concepts in mathematics. They describe relationships where the rate of change between variables is constant, represented graphically as a straight line. This simplicity makes them a central topic in algebra and calculus. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Linear Function | Linear Function
TopicLinear Functions DefinitionA linear function is a function that can be graphed as a straight line, typically written in the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionLinear functions are one of the most fundamental concepts in mathematics. They describe relationships where the rate of change between variables is constant, represented graphically as a straight line. This simplicity makes them a central topic in algebra and calculus. |
Slope-Intercept Form |
|
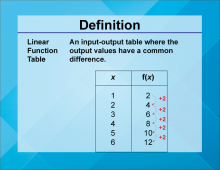
Definition--Linear Function Concepts--Linear Function Tables | Linear Function Tables
TopicLinear Functions DefinitionLinear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. DescriptionLinear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable). |
Applications of Linear Functions and Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Linear Function Tables | Linear Function Tables
TopicLinear Functions DefinitionLinear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. DescriptionLinear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable). |
Applications of Linear Functions and Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Linear Function Tables | Linear Function Tables
TopicLinear Functions DefinitionLinear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. DescriptionLinear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable). |
Applications of Linear Functions and Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Linear Function Tables | Linear Function Tables
TopicLinear Functions DefinitionLinear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. DescriptionLinear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable). |
Applications of Linear Functions and Graphs of Linear Functions |
|
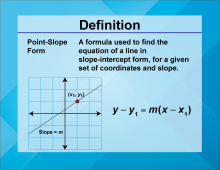
Definition--Linear Function Concepts--Point-Slope Form | Point-Slope Form
TopicLinear Functions DefinitionPoint-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. DescriptionThe point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line. |
Point-Slope Form |

|
Definition--Linear Function Concepts--Point-Slope Form | Point-Slope Form
TopicLinear Functions DefinitionPoint-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. DescriptionThe point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line. |
Point-Slope Form |

|
Definition--Linear Function Concepts--Point-Slope Form | Point-Slope Form
TopicLinear Functions DefinitionPoint-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. DescriptionThe point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line. |
Point-Slope Form |

|
Definition--Linear Function Concepts--Point-Slope Form | Point-Slope Form
TopicLinear Functions DefinitionPoint-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. DescriptionThe point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line. |
Point-Slope Form |
|
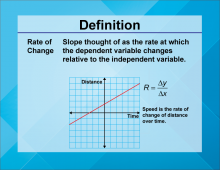
Definition--Linear Function Concepts--Rate of Change | Rate of Change
TopicLinear Functions DefinitionRate of change in a linear function is the ratio of the change in the dependent variable to the change in the independent variable, often represented as the slope m in the equation y = mx + b. DescriptionRate of change is a fundamental concept in understanding linear functions. It describes how one variable changes in relation to another, and is graphically represented by the slope of a line. |
Slope |

|
Definition--Linear Function Concepts--Rate of Change | Rate of Change
TopicLinear Functions DefinitionRate of change in a linear function is the ratio of the change in the dependent variable to the change in the independent variable, often represented as the slope m in the equation y = mx + b. DescriptionRate of change is a fundamental concept in understanding linear functions. It describes how one variable changes in relation to another, and is graphically represented by the slope of a line. |
Slope |

|
Definition--Linear Function Concepts--Rate of Change | Rate of Change
TopicLinear Functions DefinitionRate of change in a linear function is the ratio of the change in the dependent variable to the change in the independent variable, often represented as the slope m in the equation y = mx + b. DescriptionRate of change is a fundamental concept in understanding linear functions. It describes how one variable changes in relation to another, and is graphically represented by the slope of a line. |
Slope |

|
Definition--Linear Function Concepts--Slope-Intercept Form | Slope-Intercept Form
TopicLinear Functions DefinitionSlope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the y-intercept. DescriptionSlope-intercept form is one of the most commonly used forms of linear equations. It provides a clear way to understand the slope and y-intercept of a line, making it easier to graph and interpret. In real-world applications, slope-intercept form is used in various fields such as economics, physics, and engineering to model linear relationships. For example, it can represent the relationship between cost and production levels in business. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Slope-Intercept Form | Slope-Intercept Form
TopicLinear Functions DefinitionSlope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the y-intercept. DescriptionSlope-intercept form is one of the most commonly used forms of linear equations. It provides a clear way to understand the slope and y-intercept of a line, making it easier to graph and interpret. In real-world applications, slope-intercept form is used in various fields such as economics, physics, and engineering to model linear relationships. For example, it can represent the relationship between cost and production levels in business. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Slope-Intercept Form | Slope-Intercept Form
TopicLinear Functions DefinitionSlope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the y-intercept. DescriptionSlope-intercept form is one of the most commonly used forms of linear equations. It provides a clear way to understand the slope and y-intercept of a line, making it easier to graph and interpret. In real-world applications, slope-intercept form is used in various fields such as economics, physics, and engineering to model linear relationships. For example, it can represent the relationship between cost and production levels in business. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--The Equation of a Line From Two Coordinates | The Equation of a Line From Two Coordinates
TopicLinear Functions DefinitionThe equation of a line from two coordinates can be determined by finding the slope between the two points and using it in the point-slope form of a linear equation. DescriptionFinding the equation of a line from two coordinates is a fundamental skill in algebra. It involves calculating the slope between the two points and then using one of the points to form the equation in point-slope or slope-intercept form. |
Point-Slope Form |

|
Definition--Linear Function Concepts--The Equation of a Line From Two Coordinates | The Equation of a Line From Two Coordinates
TopicLinear Functions DefinitionThe equation of a line from two coordinates can be determined by finding the slope between the two points and using it in the point-slope form of a linear equation. DescriptionFinding the equation of a line from two coordinates is a fundamental skill in algebra. It involves calculating the slope between the two points and then using one of the points to form the equation in point-slope or slope-intercept form. |
Point-Slope Form |

|
Definition--Linear Function Concepts--The Equation of a Line From Two Coordinates | The Equation of a Line From Two Coordinates
TopicLinear Functions DefinitionThe equation of a line from two coordinates can be determined by finding the slope between the two points and using it in the point-slope form of a linear equation. DescriptionFinding the equation of a line from two coordinates is a fundamental skill in algebra. It involves calculating the slope between the two points and then using one of the points to form the equation in point-slope or slope-intercept form. |
Point-Slope Form |
|
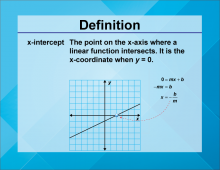
Definition--Linear Function Concepts--x-Intercept | x-Intercept
TopicLinear Functions DefinitionThe x-intercept is the point where a graph crosses the x-axis, indicating the value of x when 𝑦 y is zero. DescriptionThe x-intercept is a key concept in understanding the behavior of linear functions. It represents the point where the function's output is zero, providing insight into the function's roots and behavior. In real-world applications, the x-intercept can be used to determine break-even points in business, where revenue equals costs, or to find the time at which a process starts or stops. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--x-Intercept | x-Intercept
TopicLinear Functions DefinitionThe x-intercept is the point where a graph crosses the x-axis, indicating the value of x when 𝑦 y is zero. DescriptionThe x-intercept is a key concept in understanding the behavior of linear functions. It represents the point where the function's output is zero, providing insight into the function's roots and behavior. In real-world applications, the x-intercept can be used to determine break-even points in business, where revenue equals costs, or to find the time at which a process starts or stops. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--x-Intercept | x-Intercept
TopicLinear Functions DefinitionThe x-intercept is the point where a graph crosses the x-axis, indicating the value of x when 𝑦 y is zero. DescriptionThe x-intercept is a key concept in understanding the behavior of linear functions. It represents the point where the function's output is zero, providing insight into the function's roots and behavior. In real-world applications, the x-intercept can be used to determine break-even points in business, where revenue equals costs, or to find the time at which a process starts or stops. |
Slope-Intercept Form |
|
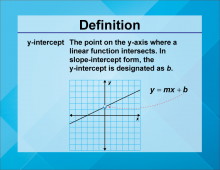
Definition--Linear Function Concepts--y-Intercept | y-Intercept
TopicLinear Functions DefinitionThe y-intercept is the point where a graph crosses the y-axis, indicating the value of y when x is zero. DescriptionThe y-intercept is a fundamental concept in understanding the behavior of linear functions. It represents the initial value of the function when the input is zero, providing insight into the function's starting point. In real-world applications, the y-intercept can be used to determine initial conditions in various scenarios, such as the starting balance in a bank account or the initial position of an object in motion. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--y-Intercept | y-Intercept
TopicLinear Functions DefinitionThe y-intercept is the point where a graph crosses the y-axis, indicating the value of y when x is zero. DescriptionThe y-intercept is a fundamental concept in understanding the behavior of linear functions. It represents the initial value of the function when the input is zero, providing insight into the function's starting point. In real-world applications, the y-intercept can be used to determine initial conditions in various scenarios, such as the starting balance in a bank account or the initial position of an object in motion. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--y-Intercept | y-Intercept
TopicLinear Functions DefinitionThe y-intercept is the point where a graph crosses the y-axis, indicating the value of y when x is zero. DescriptionThe y-intercept is a fundamental concept in understanding the behavior of linear functions. It represents the initial value of the function when the input is zero, providing insight into the function's starting point. In real-world applications, the y-intercept can be used to determine initial conditions in various scenarios, such as the starting balance in a bank account or the initial position of an object in motion. |
Slope-Intercept Form |
|
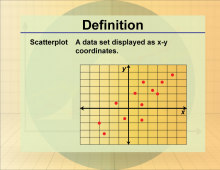
Definition--Statistics and Probability Concepts--Scatterplot | ScatterplotTopicStatistics and Probability DefinitionA scatterplot is a graphical representation of the relationship between two numerical variables. DescriptionScatterplots are essential tools in statistics for visualizing the correlation between two variables. They are widely used in fields like economics and biology to identify trends and relationships in data. For students, understanding scatterplots is important for interpreting data visually and analyzing the strength and direction of relationships between variables. This skill is crucial for developing their ability to conduct statistical analyses and draw meaningful conclusions from data. |
Data Analysis |

|
HTML5 Interactive: Data Displays | HTML5 Interactive: Data Displays
In this interactive, review seven commonly used data displays. Provides a quck review tool for a unit on data analysis. Note: the download is the Teacher's Guide. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Gathering and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Graphing a Scatterplot | In this Slide Show, learn how graph data in a scatterplot using the graph window. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Graphs of Linear Functions, Slope-Intercept Form and Data Analysis |

|
Math in the News: Issue 11--Taxing Tobacco | Math in the News: Issue 11--Taxing Tobacco
5/30/11. In this issue we look at the subject of taxation of tobacco products. Many states are using such taxes to meet budget shortfalls. What are the unintended consequences of these taxes? This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 11--Taxing Tobacco | Math in the News: Issue 11--Taxing Tobacco
5/30/11. In this issue we look at the subject of taxation of tobacco products. Many states are using such taxes to meet budget shortfalls. What are the unintended consequences of these taxes? This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 11--Taxing Tobacco | Math in the News: Issue 11--Taxing Tobacco
5/30/11. In this issue we look at the subject of taxation of tobacco products. Many states are using such taxes to meet budget shortfalls. What are the unintended consequences of these taxes? This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |