
Illustrative Math Alignment: Grade 8 Unit 8
Pythagorean Theorem and Irrational Numbers
Lesson 15: Infinite Decimal Expansions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Rationals and Radicals--Rational Functions | Rational FunctionsTopicRationals and Radicals DefinitionRational functions are functions that are the ratio of two polynomials. DescriptionRational Functions are a key concept in the study of Rational Numbers, Expressions, Equations, and Functions. These functions are the ratio of two polynomials, such as $$f(x) = \frac{P(x)}{Q(x)}$$ where P(x) and Q(x) are polynomials. Understanding rational functions involves analyzing their behavior, including identifying asymptotes, intercepts, and discontinuities. For example, the function $$f(x) = \frac{1}{x}$$ |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Rational Numbers | Rational NumbersTopicRationals and Radicals DefinitionRational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Rationalizing a Radical | Rationalizing a RadicalTopicRationals and Radicals DefinitionRationalizing a radical is the process of eliminating radicals from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. DescriptionRationalizing a Radical is an important technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves eliminating radicals from the denominator of a fraction, which simplifies the expression and often makes it easier to work with or compare to other expressions. For example, to rationalize the denominator of $$\frac{1}{\sqrt{3}}$$ |
Radical Expressions |

|
Definition--Rationals and Radicals--Rationalizing the Denominator | Rationalizing the DenominatorTopicRationals and Radicals DefinitionRationalizing the denominator is the process of eliminating radicals or complex numbers from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. DescriptionRationalizing the Denominator is a crucial technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves removing radicals or complex numbers from the denominator of a fraction, which simplifies the expression and often makes it easier to evaluate or compare with other expressions. For example, to rationalize the denominator of |
Radical Expressions |

|
Definition--Rationals and Radicals--Simplifying a Radical Expression | Simplifying a Radical ExpressionTopicRationals and Radicals DefinitionSimplifying a radical expression involves reducing the expression to its simplest form by factoring the radicand and removing any perfect square factors (for square roots) or perfect cube factors (for cube roots). DescriptionSimplifying a Radical Expression is a fundamental skill in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves reducing a radical expression to its simplest form, which often makes it easier to work with and understand. For example, simplifying $$\sqrt{18}$$ results in |
Radical Expressions |

|
Definition--Rationals and Radicals--Simplifying a Rational Expression | Simplifying a Rational ExpressionTopicRationals and Radicals DefinitionSimplifying a rational expression involves reducing the fraction to its lowest terms by factoring both the numerator and denominator and canceling common factors. DescriptionSimplifying a Rational Expression is a crucial skill in the study of Rational Numbers, Expressions, Equations, and Functions. This process involves reducing a rational expression to its simplest form by factoring both the numerator and denominator and canceling common factors. For example, simplifying $$\frac{x^2 - 1}{x - 1}$$ results in x + 1 for |
Rational Expressions |

|
Definition--Rationals and Radicals--Square Root | Square RootTopicRationals and Radicals DefinitionThe square root of a number is a value that, when multiplied by itself, gives the number. It is denoted by the radical symbol √. |
Radical Expressions |
|
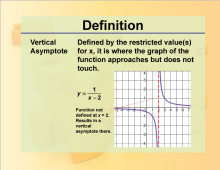
Definition--Rationals and Radicals--Vertical Asymptote | Vertical AsymptoteTopicRationals and Radicals DefinitionA vertical asymptote is a vertical line that the graph of a function approaches but never reaches as the input values get closer to a certain point. DescriptionVertical Asymptotes are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions when the denominator equals zero for certain input values, causing the function to approach infinity or negative infinity. For example, the function $$f(x) = \frac{1}{x-2}$$ |
Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 44 | INSTRUCTIONAL RESOURCE: Math Examples--Rational Expressions
The complete set of 28 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Expressions and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Pumpkin PI | In this Slide Show, do a hands-on geometry activity to measure π. Note: The download is a PPT file. |
Ratios and Rates |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 8)--Lesson 1--Understanding Ratios, Proportional Relationships, and Rational Numbers | Lesson Plan: Ratios and Proportional Relationships In this lesson, students explore ratios and proportional relationships, building on their prior knowledge to deepen their understanding of proportional reasoning. They will analyze proportional relationships in tables, graphs, and equations while identifying the constant of proportionality and its significance in real-world applications. Key concepts covered in this lesson include: |
Ratios and Rates, Percents and Proportions |
|
Math Clip Art--Number Systems--Rational Numbers 01 | Math Clip Art--Number Systems--Rational Numbers 01
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 02 | Math Clip Art--Number Systems--Rational Numbers 02
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 03 | Math Clip Art--Number Systems--Rational Numbers 03
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 04 | Math Clip Art--Number Systems--Rational Numbers 04
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 05 | Math Clip Art--Number Systems--Rational Numbers 05
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 06 | Math Clip Art--Number Systems--Rational Numbers 06
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
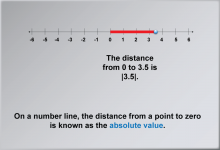
Math Clip Art--Number Systems--Rational Numbers 07 | Math Clip Art--Number Systems--Rational Numbers 07
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |
|
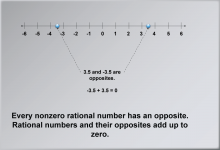
Math Clip Art--Number Systems--Rational Numbers 08 | Math Clip Art--Number Systems--Rational Numbers 08
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |
|
Math Clip Art--Number Systems--Rational Numbers 09 | Math Clip Art--Number Systems--Rational Numbers 09
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 10 | Math Clip Art--Number Systems--Rational Numbers 10
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 11 | Math Clip Art--Number Systems--Rational Numbers 11
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 1 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 1TopicExponents DescriptionShows Example 1 with the expression 32. The solution explains how to simplify by multiplying 3 by itself according to the exponent. Example 1: Simplify 32. Multiply 3 by itself two times: 3•3 = 9. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 10 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 10TopicExponents DescriptionShows Example 10 with the expression (-3)3•54. The solution uses order of operations to evaluate each term before multiplying. Example 10: Simplify (-3)3•54. Evaluate each exponential term separately, then multiply: -27•625= -16,875. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 11 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 11TopicExponents DescriptionExample 11 shows how to simplify (1/2)2. The image illustrates multiplying 1/2 by itself due to the exponent of 2. Example 11: Simplify (1/2)2. Multiply one-half two times. Solution: (1/2) * (1/2) = 1/4. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 12 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 12TopicExponents DescriptionExample 12 shows how to simplify (1/3)4. The image illustrates multiplying 1/3 four times due to the exponent of 4. Example 12: Simplify (1/3)4. Multiply one-third four times. Solution: (1/3) * (1/3) * (1/3) * (1/3) = 1/81. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 13 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 13TopicExponents DescriptionExample 13 shows how to simplify (-1/3)3. The image illustrates multiplying -1/3 three times due to the exponent of 3. Example 13: Simplify (-1/3)3. Multiply negative one-third three times. Solution: (-1/3) * (-1/3) * (-1/3) = -1/27. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 14 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 14TopicExponents DescriptionExample 14 shows how to simplify 2-1. The image illustrates rewriting 2-1 as the reciprocal of 2 raised to the first power. Example 14: Simplify 2-1. Negative exponents are written as reciprocals. Solution: 2-1 = 1/2. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 15 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 15TopicExponents DescriptionExample 15 shows how to simplify 2-2. The image illustrates rewriting 2-2 as the reciprocal of 2 raised to the second power. Example 15: Simplify 2-2. Negative exponents are written as reciprocals. Solution: 2-2 = 1/(22) = 1/4. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 2 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 2TopicExponents DescriptionShows Example 2 with the expression 43. The solution explains the simplification by multiplying 4 three times. Example 2: Simplify 43. Multiply 4 by itself three times: 4•4•4 = 64. In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 3 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 3TopicExponents DescriptionShows Example 3 with the expression 54. The solution details multiplying 5 four times. Example 3: Simplify 54. Multiply 5 by itself four times: 5•5•5•5 = 625. In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 4 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 4TopicExponents DescriptionShows Example 4 with the expression 106. The solution simplifies by multiplying 10 six times. Example 4: Simplify 106. Multiply 10 by itself six times: 10•10•10•10•10•10 = 1,000,000. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 5 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 5TopicExponents DescriptionShows Example 5 with the expression (-1)2. The solution explains the result by multiplying -1 by itself. Example 5: Simplify (-1)2. Multiply -1 by itself two times: (-1)•(-1) = 1. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 6 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 6TopicExponents DescriptionShows Example 6 with the expression (-5)3. The solution demonstrates multiplying -5 three times. Example 6: Simplify (_5)3. Multiply -5 by itself three times: (-5)•(-5)•(-5) = -125. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 7 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 7TopicExponents DescriptionShows Example 7 with the expression (-6)4. The solution explains multiplying -6 by itself four times. Example 7: Simplify (-6)4. Multiply -6 by itself four times: (-6)•(-6)•(-6)•(-6) = 1296. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 8 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 8TopicExponents DescriptionShows Example 8 with the expression 23•32. The solution demonstrates using order of operations to simplify each term separately, then multiply. Example 8: Simplify 23•32. Evaluate each exponential term separately, then multiply: 8•9 = 72. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 9 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 9TopicExponents DescriptionShows Example 9 with the expression (-1)2•43. The solution explains simplifying each term individually before multiplying. Example 9: Simplify (-1)2•43. Evaluate each exponential term separately, then multiply: 1•64 = 64. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 1 | Math Example--Numerical Expressions--Dividing Integers: Example 1TopicNumerical Expressions DescriptionThis example demonstrates the division of two positive integers: 12 divided by 3. The solution shows that when dividing one integer by another, the result is a rational number. In this case, with two positive integers, the quotient is positive. The calculation is presented as 12 ÷ 3 = 12 / 3 = 4. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 10 | Math Example--Numerical Expressions--Dividing Integers: Example 10TopicNumerical Expressions DescriptionThis example demonstrates the division of three integers: (-144) ÷ 12 ÷ (-2). The solution shows that dividing three integers, two negative and one positive, results in a positive quotient. The calculation is presented step-by-step: (-144) ÷ 12 ÷ (-2) = -12 / -2 = 6. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 11 | Math Example--Numerical Expressions--Dividing Integers: Example 11TopicNumerical Expressions DescriptionThis example demonstrates the division of three integers: (-150) ÷ (-5) ÷ 3. The solution shows that dividing three integers, two negative and one positive, results in a positive quotient. The calculation is presented step-by-step: (-150) ÷ (-5) ÷ 3 = 30 / 3 = 10. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 12 | Math Example--Numerical Expressions--Dividing Integers: Example 12TopicNumerical Expressions DescriptionThis example illustrates the division of three negative integers: -108 ÷ (-2) ÷ (-6). The solution demonstrates that dividing three negative integers results in a negative quotient. The calculation is presented step-by-step: (-108 / -2) / -6 = 54 / -6 = -9. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 13 | Math Example--Numerical Expressions--Dividing Integers: Example 13TopicNumerical Expressions DescriptionThis example demonstrates the division of two positive integers: 12 ÷ 5. The solution shows that dividing two positive integers results in a positive quotient, which in this case is a mixed number. The calculation is presented as: 12 / 5 = 2 2/5. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 14 | Math Example--Numerical Expressions--Dividing Integers: Example 14TopicNumerical Expressions DescriptionThis example illustrates the division of a positive integer by a negative integer: 14 ÷ (-6). The solution demonstrates that dividing a positive by a negative results in a negative quotient, which in this case is a mixed number. The calculation is presented as: 14 / -6 = -2 1/3. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 15 | Math Example--Numerical Expressions--Dividing Integers: Example 15TopicNumerical Expressions DescriptionThis example demonstrates the division of a negative integer by a positive integer: -18 ÷ 4. The solution shows that dividing a negative by a positive results in a negative quotient, which in this case is a fraction. The calculation is presented as: -18 / 4 = -9/2 = -4 1/2. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 16 | Math Example--Numerical Expressions--Dividing Integers: Example 16TopicNumerical Expressions DescriptionThis example illustrates the division of two negative integers: (-9) ÷ (-6). The solution demonstrates that dividing two negative integers results in a positive fraction. The calculation is presented step-by-step: (-9) ÷ (-6) = -9 / -6 = -3 / -2 = 1 1/2. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 17 | Math Example--Numerical Expressions--Dividing Integers: Example 17TopicNumerical Expressions DescriptionThis example demonstrates the division of three positive integers: 20 ÷ 2 ÷ 4. The solution shows that dividing three positive integers results in a positive mixed number quotient. The calculation is presented step-by-step: 20 ÷ 2 ÷ 4 = 20 / 2 / 4 = 10 / 4 = 2 1/2. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 18 | Math Example--Numerical Expressions--Dividing Integers: Example 18TopicNumerical Expressions DescriptionThis example illustrates the division of three integers: 48 ÷ 6 ÷ (-3). The solution demonstrates that dividing two positive integers and one negative integer results in a negative mixed number quotient. The calculation is presented step-by-step: 48 ÷ 6 ÷ (-3) = 48 / 6 / (-3) = 8 / (-3) = -2 2/3. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 19 | Math Example--Numerical Expressions--Dividing Integers: Example 19TopicNumerical Expressions DescriptionThis example demonstrates the division of three integers: 24 ÷ (-6) ÷ 2. The solution shows that dividing two positive integers and one negative integer results in a negative quotient. The calculation is presented step-by-step: 24 ÷ (-6) ÷ 2 = 24 / (-6) / (2) = -4 / 2 = -2. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 2 | Math Example--Numerical Expressions--Dividing Integers: Example 2TopicNumerical Expressions DescriptionThis example illustrates the division of a positive integer by a negative integer: 14 divided by -7. The solution demonstrates that when dividing one integer by another, the result is a rational number. In this case, when dividing a positive integer by a negative integer, the quotient is negative. The calculation is presented as 14 ÷ (-7) = 14 / -7 = -2. |
Numerical Expressions |

|
Math Example--Numerical Expressions--Dividing Integers: Example 20 | Math Example--Numerical Expressions--Dividing Integers: Example 20TopicNumerical Expressions DescriptionThis example demonstrates the division of three integers: (-72) / 2 / 5. The solution shows that dividing a negative integer by two positive integers results in a negative mixed number quotient. The calculation is presented step-by-step: (-72) / 2 / 5 = -72 / (2 * 5) = -36 / 5 = -7 1/5. |
Numerical Expressions |