
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 16: Applying Volume and Surface Area
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Animated Math Clip Art--3D Geometry--Surface Area | Surface AreaTopic3D Geometry DescriptionThis animation illustrates the concept of surface area for a 3D shape. It shows how the surface of a three-dimensional object can be "unfolded" or "unwrapped" to reveal all its faces or surfaces, which can then be measured to calculate the total surface area. Using animated math clip art like this helps students visualize the abstract concept of surface area. Teachers can use this to explain how to calculate surface area for various 3D shapes and discuss real-world applications of this concept. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Surface Area | Surface Area of 3D FiguresTopic3D Geometry DefinitionSurface area is the total area that the surface of a three-dimensional object occupies. DescriptionIn the realm of three-dimensional geometry, surface area is a fundamental concept that quantifies the extent of a 3D shape's exterior surface. This measure is crucial for various applications, including engineering, architecture, and everyday tasks. For example, when painting a room, the surface area of the walls, ceiling, and floor must be calculated to determine the amount of paint required. |
Surface Area |

|
Formulas--Surface Area of a Cube | Formulas--Surface Area of a Cube
The formula for the Surface Area of a Cube. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Formulas--Surface Area of a Cylinder | Formulas--Surface Area of a Cylinder
The formula for the Surface Area of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area and Cylinders |
|
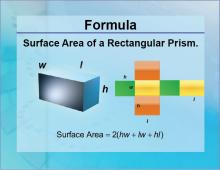
Formulas--Surface Area of a Rectangular Prism | Formulas--Surface Area of a Rectangular Prism
The formula for the Surface Area of a Rectangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Formulas--Surface Area of a Sphere | Formulas--Surface Area of a Sphere
The formula for the Surface Area of a Sphere. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
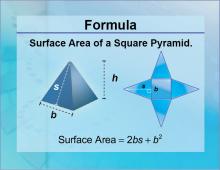
Formulas--Surface Area of a Square Pyramid | Formulas--Surface Area of a Square Pyramid
The formula for the Surface Area of a Square Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
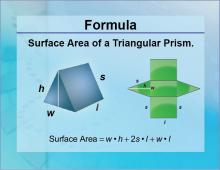
Formulas--Surface Area of a Triangular Prism | Formulas--Surface Area of a Triangular Prism
The formula for the Surface Area of a Triangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
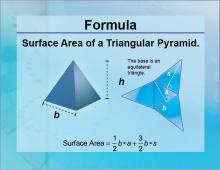
Formulas--Surface Area of a Triangular Pyramid | Formulas--Surface Area of a Triangular Pyramid
The formula for the Surface Area of a Triangular Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
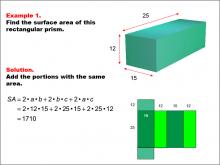
|
Math Example--Area and Perimeter--Surface Area: Example 1 | Math Example--Area and Perimeter--Surface Area: Example 1TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular prism. The prism has dimensions of 25, 15, and 12 units. The surface area is determined by summing the areas of all faces, which is represented by the formula SA = 2ab + 2bc + 2ac. For this specific prism, the calculation yields a surface area of 1710 square units. |
Surface Area |
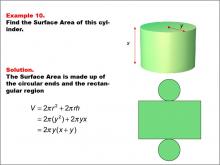
|
Math Example--Area and Perimeter--Surface Area: Example 10 | Math Example--Area and Perimeter--Surface Area: Example 10TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cylinder with radius y and height x. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, which simplifies to SA = 2πy(x + y), where y is the radius and x is the height of the cylinder. |
Surface Area |
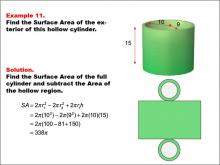
|
Math Example--Area and Perimeter--Surface Area: Example 11 | Math Example--Area and Perimeter--Surface Area: Example 11TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The surface area is determined by subtracting the area of the hollow region from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, where r1 is the outer radius and r2 is the inner radius. For this specific hollow cylinder, the calculation yields a surface area of 338π square units. |
Surface Area |
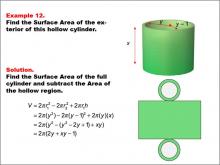
|
Math Example--Area and Perimeter--Surface Area: Example 12 | Math Example--Area and Perimeter--Surface Area: Example 12TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cylinder with an outer radius y, an inner radius y - 1, and a height x. The surface area is determined by subtracting the hollow region's area from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, which simplifies to SA = 2π(2y + xy - 1), where r1 is the outer radius (y) and r2 is the inner radius (y - 1). |
Surface Area |
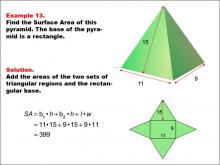
|
Math Example--Area and Perimeter--Surface Area: Example 13 | Math Example--Area and Perimeter--Surface Area: Example 13TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular-based pyramid with dimensions 11, 9, and 15 units. The pyramid is depicted with its net unfolded, showing two triangular faces and a rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, where b1 and b2 are the bases of the triangular faces, h is the height of the triangular faces, and l and w are the length and width of the rectangular base. For this specific pyramid, the calculation yields a surface area of 399 square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 14 | Math Example--Area and Perimeter--Surface Area: Example 14TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a rectangular-based pyramid with dimensions labeled as x, y, and z. The pyramid is depicted with its net unfolded into two triangular faces and one rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, which simplifies to SA = xz + yz + xy, where x and y are the dimensions of the rectangular base, and z is the height of the triangular faces. |
Surface Area |
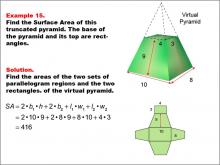
|
Math Example--Area and Perimeter--Surface Area: Example 15 | Math Example--Area and Perimeter--Surface Area: Example 15TopicSurface Area |
Surface Area |
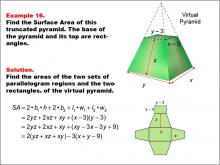
|
Math Example--Area and Perimeter--Surface Area: Example 16 | Math Example--Area and Perimeter--Surface Area: Example 16TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a truncated rectangular-based pyramid with dimensions labeled as x - 3, y - 3, z, x, and y. The virtual pyramid is shown with its net unfolded into four parallelogram regions and two rectangles. The surface area is calculated using the formula SA = 2yz + 2xz + xy + (x - 3)(y - 3), which simplifies to SA = (yz + xz + xy) - (x + y - 9). |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 17 | Math Example--Area and Perimeter--Surface Area: Example 17TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a sphere with a radius of 3 units. The surface area is calculated using the formula SA = 4πr2, where r is the radius of the sphere. For this specific sphere, the calculation yields a surface area of 36π square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 18 | Math Example--Area and Perimeter--Surface Area: Example 18TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a sphere with an unknown radius labeled as "x". The surface area is calculated using the formula SA = 4πr2, which in this case becomes SA = 4πx2, where x is the radius of the sphere. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 19 | Math Example--Area and Perimeter--Surface Area: Example 19TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cube with a side length of 7 units. The surface area is calculated using the formula SA = 6s2, where s is the length of one side of the cube. For this specific cube, the calculation yields a surface area of 294 square units. |
Surface Area |
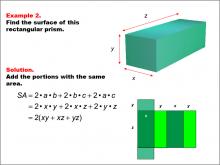
|
Math Example--Area and Perimeter--Surface Area: Example 2 | Math Example--Area and Perimeter--Surface Area: Example 2TopicSurface Area DescriptionThis example introduces a general formula for calculating the surface area of a rectangular prism with dimensions x, y, and z. The surface area is computed using the formula SA = 2xy + 2xz + 2yz, which can be simplified to 2(xy + xz + yz). This generalized approach allows for easy application to prisms of various sizes. Surface area calculations are fundamental in mathematics, with applications ranging from manufacturing to environmental science. This collection of examples aids in teaching the topic by presenting both specific and general cases, helping students understand how to apply formulas flexibly to different scenarios. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 20 | Math Example--Area and Perimeter--Surface Area: Example 20TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cube with an unknown side length labeled as "x". The surface area is calculated using the formula SA = 6s2, which in this case becomes SA = 6x2, where x is the length of one side of the cube. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 21 | Math Example--Area and Perimeter--Surface Area: Example 21TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cube with an outer side length of 9 units and an inner hollow square side length of 7 units. The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 is the outer side length and s2 is the inner side length. For this specific hollow cube, the calculation yields a surface area of 388 square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 22 | Math Example--Area and Perimeter--Surface Area: Example 22TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cube with variable dimensions. The outer side length is labeled as "x" and the inner hollow side length as "x - 2". The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 = x and s2 = x - 2. After expanding and simplifying, the result is SA = 4(x2 + 2x - 2) square units. |
Surface Area |
|
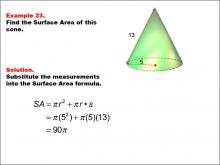
Math Example--Area and Perimeter--Surface Area: Example 23 | Math Example--Area and Perimeter--Surface Area: Example 23TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cone with a radius of 5 units and a slant height of 13 units. The surface area is calculated using the formula SA = π * r2 + π * r * s, where r is the radius and s is the slant height. For this specific cone, the calculation yields a surface area of 90π square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 24 | Math Example--Area and Perimeter--Surface Area: Example 24TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cone with variable dimensions. The radius is labeled as "x" and the slant height as "y". The surface area is calculated using the formula SA = π * r2 + π * r * s, where r = x and s = y. This simplifies to SA = π * x(x + y) square units. |
Surface Area |
|
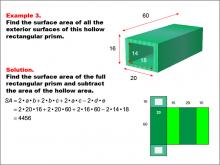
Math Example--Area and Perimeter--Surface Area: Example 3 | Math Example--Area and Perimeter--Surface Area: Example 3TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow rectangular prism. The outer dimensions are 60, 20, and 16 units, while the inner dimensions are 18 and 14 units. The surface area is determined by subtracting the area of the hollow region from the surface area of the full rectangular prism, resulting in a surface area of 4456 square units. |
Surface Area |
|
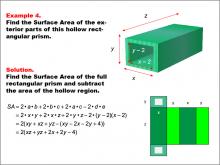
Math Example--Area and Perimeter--Surface Area: Example 4 | Math Example--Area and Perimeter--Surface Area: Example 4TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow rectangular prism. The outer dimensions are represented by x, y, and z, while the hollow dimensions are represented by (y - 2) and (x - 2). The surface area is determined by subtracting the hollow region's surface area from that of the full rectangular prism, resulting in the formula SA = 2(xz + yz + 2x + 2y - 4). |
Surface Area |
|
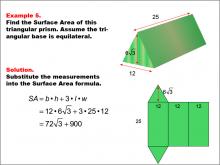
Math Example--Area and Perimeter--Surface Area: Example 5 | Math Example--Area and Perimeter--Surface Area: Example 5TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a triangular prism with an equilateral triangular base. The base is 12 units, the height is 6 * √(3), and the length of the prism is 25 units. The surface area is calculated using the formula SA = b * h + 3 * l * w, where b is the base, h is the height of the triangle, l is the length of the prism, and w is the width of the triangle. The final result is 72 * √(3) + 900 square units. |
Surface Area |
|
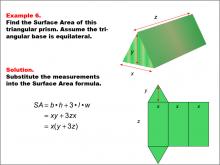
Math Example--Area and Perimeter--Surface Area: Example 6 | Math Example--Area and Perimeter--Surface Area: Example 6TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a triangular prism with an equilateral triangular base. The dimensions are represented by x for the base, y for the height of the triangle, and z for the length of the prism. The surface area is determined using the formula SA = b * h + 3 * l * w, which simplifies to SA = xy + 3zx = x(y + 3z). |
Surface Area |
|
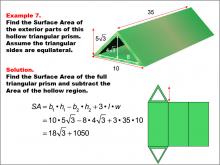
Math Example--Area and Perimeter--Surface Area: Example 7 | Math Example--Area and Perimeter--Surface Area: Example 7TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow triangular prism with an equilateral triangular base. The outer triangle has a base of 10 units and a height of 5 * √(3), while the inner triangle has a base of 8 units and a height of 4 * √(3). The length of the prism is 35 units. The surface area is calculated by subtracting the area of the hollow region from the full prism's surface area, resulting in SA = b1 * h1 - b2 * h2 + 3 * l * w = (18 * √(3)) + 1050 square units. |
Surface Area |
|
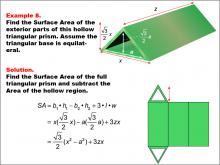
Math Example--Area and Perimeter--Surface Area: Example 8 | Math Example--Area and Perimeter--Surface Area: Example 8TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow triangular prism with an equilateral triangular base. The outer triangle has a base labeled as x, and the inner triangle has a base labeled as a. The heights are given as √(3)/2 for both triangles, and the length of the prism is z units. The surface area is determined by subtracting the area of the hollow region from the full prism's surface area, resulting in the formula SA = (√(3)/2) (x2 - a2) + 3zx. |
Surface Area |
|
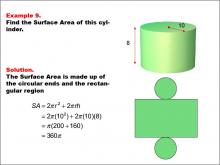
Math Example--Area and Perimeter--Surface Area: Example 9 | Math Example--Area and Perimeter--Surface Area: Example 9TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cylinder with a radius of 10 units and a height of 8 units. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, where r is the radius and h is the height. For this specific cylinder, the calculation yields a surface area of 360π square units. |
Surface Area |
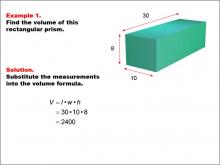
|
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
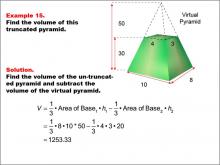
|
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
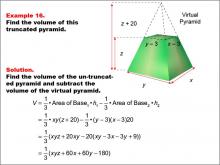
|
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |
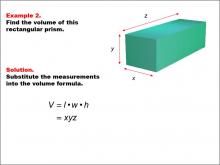
|
Math Example--Volume Concepts--Calculating Volume: Example 2 | Math Example--Volume Concepts--Calculating Volume: Example 2TopicVolume DescriptionA rectangular prism with dimensions labeled as x, y, and z. The image shows a general example of calculating the volume of a rectangular prism using variables instead of specific numbers. This image illustrates Example 2: The caption describes how to find the volume of a rectangular prism using variables for length (x), width (y), and height (z). The formula is given as V = x * y * z, but no specific values are provided. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 20 | Math Example--Volume Concepts--Calculating Volume: Example 20TopicVolume DescriptionA green cube with side length labeled as x. This image is part of a math example showing how to calculate the volume of a cube using an unknown side length. This image illustrates Example 20: The text explains how to find the volume of a cube with an unknown side length x. The formula used is V = s3, and substituting s = x gives V = x3. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 21 | Math Example--Volume Concepts--Calculating Volume: Example 21TopicVolume DescriptionA hollow cube with an outer edge of 9 and an inner hollow region with an edge of 7. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 21: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 is the outer edge (9) and s2 is the inner edge (7). The solution calculates 9^3 - 7^3 = 386.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 22 | Math Example--Volume Concepts--Calculating Volume: Example 22TopicVolume DescriptionA hollow cube with an outer edge of x and an inner hollow region with an edge of x - 2. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 22: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 = x and s2 = x - 2. Expanding and simplifying gives V = 6x2 - 12x + 8. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 23 | Math Example--Volume Concepts--Calculating Volume: Example 23TopicVolume Description
A cone with a height of 12 and a radius of 4. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 23: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = 4 and h = 12. Substituting these values gives V = (1/3) * π * (42) * 12 = 64π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 24 | Math Example--Volume Concepts--Calculating Volume: Example 24TopicVolume DescriptionA cone with a height labeled as y and a radius labeled as x. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 24: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = x and h = y. Substituting these variables gives V = (x^2 * y)/3 * π. |
Volume |