
Illustrative Math Alignment: Grade 6 Unit 1
Reasoning to Find Area
Lesson 18: Surface Area of a Cube
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Closed Captioned Video: Geometry Applications: Area and Volume |
Closed Captioned Video: Geometry Applications: Area and VolumeTopicArea and Volume |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 |
Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 |
Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 |
Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Definition--3D Geometry Concepts--Surface Area |
Surface Area of 3D FiguresTopic3D Geometry DefinitionSurface area is the total area that the surface of a three-dimensional object occupies. DescriptionIn the realm of three-dimensional geometry, surface area is a fundamental concept that quantifies the extent of a 3D shape's exterior surface. This measure is crucial for various applications, including engineering, architecture, and everyday tasks. For example, when painting a room, the surface area of the walls, ceiling, and floor must be calculated to determine the amount of paint required. |
Surface Area |
|
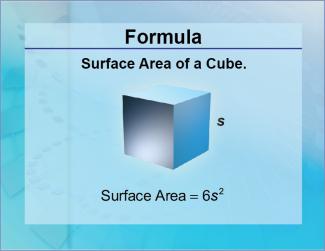
Formulas--Surface Area of a Cube |
Formulas--Surface Area of a Cube
The formula for the Surface Area of a Cube. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
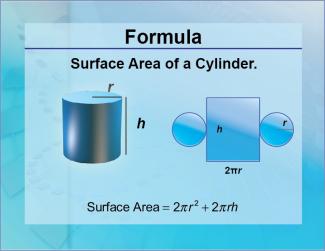
Formulas--Surface Area of a Cylinder |
Formulas--Surface Area of a Cylinder
The formula for the Surface Area of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area and Cylinders |
|
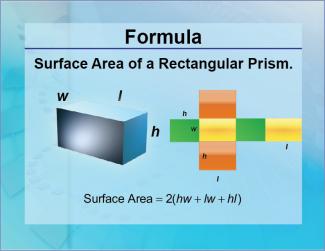
Formulas--Surface Area of a Rectangular Prism |
Formulas--Surface Area of a Rectangular Prism
The formula for the Surface Area of a Rectangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Formulas--Surface Area of a Sphere |
Formulas--Surface Area of a Sphere
The formula for the Surface Area of a Sphere. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
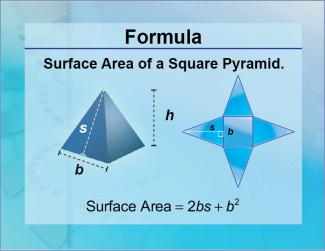
Formulas--Surface Area of a Square Pyramid |
Formulas--Surface Area of a Square Pyramid
The formula for the Surface Area of a Square Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
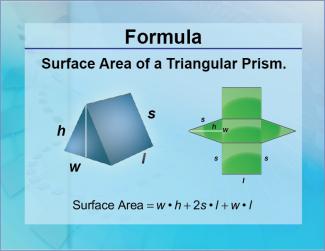
Formulas--Surface Area of a Triangular Prism |
Formulas--Surface Area of a Triangular Prism
The formula for the Surface Area of a Triangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
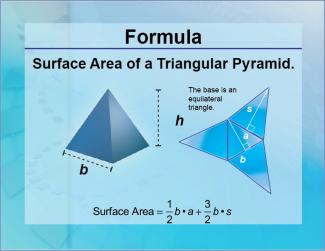
Formulas--Surface Area of a Triangular Pyramid |
Formulas--Surface Area of a Triangular Pyramid
The formula for the Surface Area of a Triangular Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2 |
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2TopicGeometric Models |
Surface Area, Volume and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 55 |
INSTRUCTIONAL RESOURCE: Math Examples--Surface Area
This set of tutorials provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Surface Area |
|
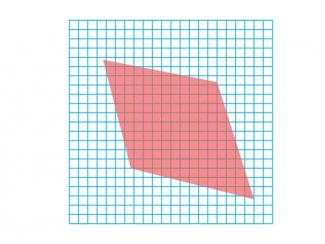
Math Clip Art--Geometry Concepts--Area Estimation 1 |
Math Clip Art--Area Estimation 1TopicGeometry Concepts DescriptionThis image presents an irregular polygon superimposed on a square grid. The grid serves as a crucial tool for estimating the area of the polygon by providing a systematic method of counting squares. To estimate the area, students should count the number of full squares entirely contained within the irregular polygon. For partial squares intersected by the polygon's edges, they need to approximate what fraction of each square is covered. By summing these full and partial square counts, students can arrive at a reasonable estimate of the polygon's area. |
Surface Area |

|
Math Clip Art--Geometry Concepts--Area Estimation 10 |
Math Clip Art--Area Estimation 10TopicGeometry Concepts DescriptionThis image showcases another closed curve area superimposed on a square grid. The grid acts as a vital tool for estimating the area enclosed by the curve through a square-counting method. To estimate the area, students should begin by counting the number of whole squares that are completely enclosed within the closed curve. For squares that are partially covered by the curve, students need to approximate what fraction of each square is included. By combining these full and partial square counts, students can arrive at a reasonable estimate of the area within the closed curve. |
Surface Area |

|
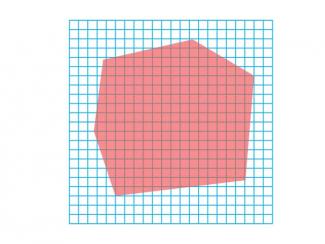
Math Clip Art--Geometry Concepts--Area Estimation 2 |
Math Clip Art--Area Estimation 2TopicGeometry Concepts DescriptionThis image showcases another irregular polygon overlaid on a square grid. The grid functions as an essential tool for estimating the area of the polygon through a square-counting method. To estimate the area, students should first count the number of complete squares that fall entirely within the boundaries of the irregular polygon. For squares that are only partially covered by the polygon, students need to assess what fraction of each square is included. By adding these full and partial square counts, students can develop a reasonable estimate of the polygon's total area. |
Surface Area |
|
Math Clip Art--Geometry Concepts--Area Estimation 3 |
Math Clip Art--Area Estimation 3TopicGeometry Concepts DescriptionThis image depicts an irregular polygon placed on a square grid. The grid acts as a vital tool for estimating the area of the polygon using a square-counting approach. To estimate the area, students should begin by counting the number of whole squares that are completely enclosed within the irregular polygon. For squares that are partially covered by the polygon's edges, students need to approximate what portion of each square is included. By combining these full and partial square counts, students can arrive at a reasonable estimate of the polygon's total area. |
Surface Area |
|
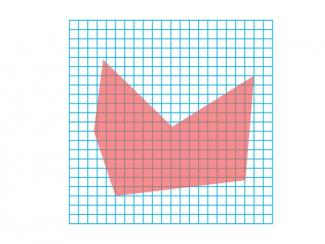
Math Clip Art--Geometry Concepts--Area Estimation 4 |
Math Clip Art--Area Estimation 4TopicGeometry Concepts DescriptionThis image features an irregular polygon superimposed on a square grid. The grid serves as a crucial tool for estimating the area of the polygon through a square-counting method. To estimate the area, students should first count the number of complete squares that fall entirely within the boundaries of the irregular polygon. For squares that are only partially covered by the polygon, students need to assess what fraction of each square is included. By summing these full and partial square counts, students can develop a reasonable estimate of the polygon's total area. |
Surface Area |

|
Math Clip Art--Geometry Concepts--Area Estimation 5 |
Math Clip Art--Area Estimation 5TopicGeometry Concepts DescriptionThis image showcases a closed curve area outlined on a square grid. The grid functions as an essential tool for estimating the area enclosed by the curve through a square-counting approach. To estimate the area, students should first count the number of complete squares that fall entirely within the closed curve. For squares that are only partially enclosed by the curve, students need to assess what fraction of each square is included. By adding these full and partial square counts, students can develop a reasonable estimate of the total area within the closed curve. |
Surface Area |

|
Math Clip Art--Geometry Concepts--Area Estimation 6 |
Math Clip Art--Area Estimation 6TopicGeometry Concepts DescriptionThis image presents a closed curve area superimposed on a square grid. The grid serves as a crucial tool for estimating the area enclosed by the curve using a square-counting method. To estimate the area, students should begin by counting the number of whole squares that are completely enclosed within the closed curve. For squares that are partially covered by the curve, students need to approximate what portion of each square is included. By combining these full and partial square counts, students can arrive at a reasonable estimate of the total area within the closed curve. |
Surface Area |
|
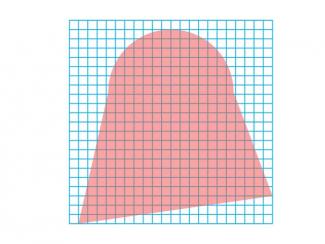
Math Clip Art--Geometry Concepts--Area Estimation 7 |
Math Clip Art--Area Estimation 7TopicGeometry Concepts DescriptionThis image features a closed curve area outlined on a square grid. The grid acts as a vital tool for estimating the area enclosed by the curve through a square-counting approach. To estimate the area, students should first count the number of complete squares that fall entirely within the closed curve. For squares that are only partially enclosed by the curve, students need to assess what fraction of each square is included. By summing these full and partial square counts, students can develop a reasonable estimate of the total area within the closed curve. |
Surface Area |
|
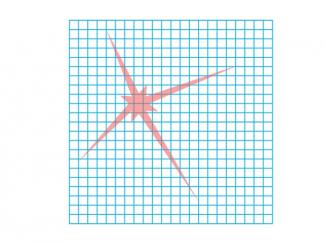
Math Clip Art--Geometry Concepts--Area Estimation 8 |
Math Clip Art--Area Estimation 8TopicGeometry Concepts DescriptionThis image depicts a radiating figure superimposed on a square grid. The grid serves as an essential tool for estimating the area of the figure using a square-counting method. To estimate the area, students should begin by counting the number of whole squares that are completely enclosed within the radiating figure. For squares that are partially covered by the figure's edges, students need to approximate what portion of each square is included. By combining these full and partial square counts, students can arrive at a reasonable estimate of the figure's total area. |
Surface Area |
|
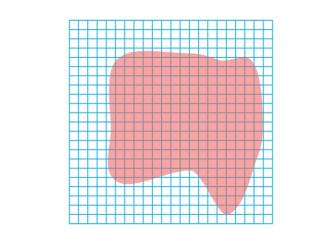
Math Clip Art--Geometry Concepts--Area Estimation 9 |
Math Clip Art--Area Estimation 9TopicGeometry Concepts DescriptionThis image presents a closed curve area outlined on a square grid. The grid functions as a crucial tool for estimating the area enclosed by the curve using a square-counting approach. To estimate the area, students should first count the number of complete squares that fall entirely within the closed curve. For squares that are only partially enclosed by the curve, students need to assess what fraction of each square is included. By summing these full and partial square counts, students can develop a reasonable estimate of the total area within the closed curve. |
Surface Area |
|
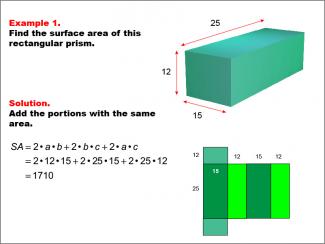
Math Example--Area and Perimeter--Surface Area: Example 1 |
Math Example--Area and Perimeter--Surface Area: Example 1TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular prism. The prism has dimensions of 25, 15, and 12 units. The surface area is determined by summing the areas of all faces, which is represented by the formula SA = 2ab + 2bc + 2ac. For this specific prism, the calculation yields a surface area of 1710 square units. |
Surface Area |
|
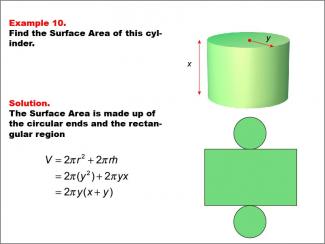
Math Example--Area and Perimeter--Surface Area: Example 10 |
Math Example--Area and Perimeter--Surface Area: Example 10TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cylinder with radius y and height x. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, which simplifies to SA = 2πy(x + y), where y is the radius and x is the height of the cylinder. |
Surface Area |
|
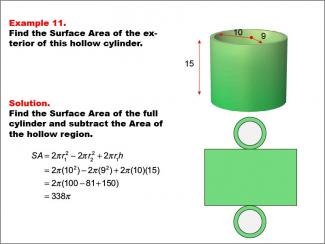
Math Example--Area and Perimeter--Surface Area: Example 11 |
Math Example--Area and Perimeter--Surface Area: Example 11TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The surface area is determined by subtracting the area of the hollow region from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, where r1 is the outer radius and r2 is the inner radius. For this specific hollow cylinder, the calculation yields a surface area of 338π square units. |
Surface Area |
|
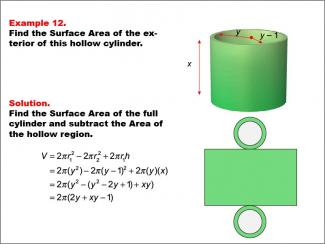
Math Example--Area and Perimeter--Surface Area: Example 12 |
Math Example--Area and Perimeter--Surface Area: Example 12TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cylinder with an outer radius y, an inner radius y - 1, and a height x. The surface area is determined by subtracting the hollow region's area from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, which simplifies to SA = 2π(2y + xy - 1), where r1 is the outer radius (y) and r2 is the inner radius (y - 1). |
Surface Area |
|
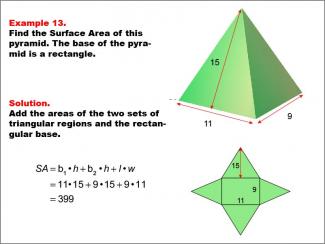
Math Example--Area and Perimeter--Surface Area: Example 13 |
Math Example--Area and Perimeter--Surface Area: Example 13TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular-based pyramid with dimensions 11, 9, and 15 units. The pyramid is depicted with its net unfolded, showing two triangular faces and a rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, where b1 and b2 are the bases of the triangular faces, h is the height of the triangular faces, and l and w are the length and width of the rectangular base. For this specific pyramid, the calculation yields a surface area of 399 square units. |
Surface Area |
|
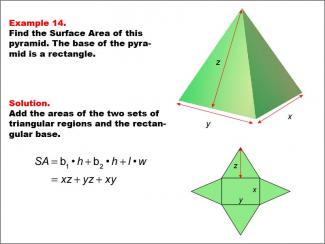
Math Example--Area and Perimeter--Surface Area: Example 14 |
Math Example--Area and Perimeter--Surface Area: Example 14TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a rectangular-based pyramid with dimensions labeled as x, y, and z. The pyramid is depicted with its net unfolded into two triangular faces and one rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, which simplifies to SA = xz + yz + xy, where x and y are the dimensions of the rectangular base, and z is the height of the triangular faces. |
Surface Area |
|
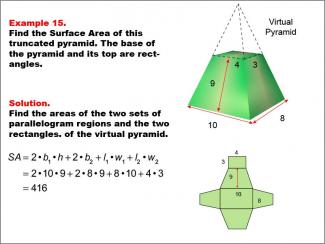
Math Example--Area and Perimeter--Surface Area: Example 15 |
Math Example--Area and Perimeter--Surface Area: Example 15TopicSurface Area |
Surface Area |
|
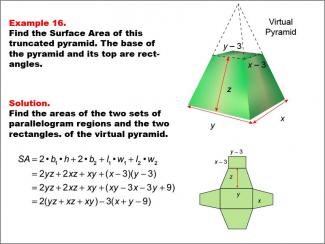
Math Example--Area and Perimeter--Surface Area: Example 16 |
Math Example--Area and Perimeter--Surface Area: Example 16TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a truncated rectangular-based pyramid with dimensions labeled as x - 3, y - 3, z, x, and y. The virtual pyramid is shown with its net unfolded into four parallelogram regions and two rectangles. The surface area is calculated using the formula SA = 2yz + 2xz + xy + (x - 3)(y - 3), which simplifies to SA = (yz + xz + xy) - (x + y - 9). |
Surface Area |
|
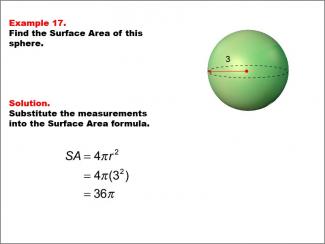
Math Example--Area and Perimeter--Surface Area: Example 17 |
Math Example--Area and Perimeter--Surface Area: Example 17TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a sphere with a radius of 3 units. The surface area is calculated using the formula SA = 4πr2, where r is the radius of the sphere. For this specific sphere, the calculation yields a surface area of 36π square units. |
Surface Area |
|
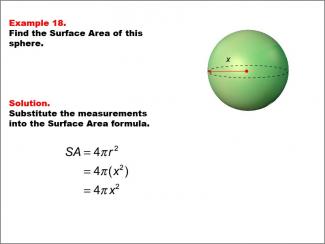
Math Example--Area and Perimeter--Surface Area: Example 18 |
Math Example--Area and Perimeter--Surface Area: Example 18TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a sphere with an unknown radius labeled as "x". The surface area is calculated using the formula SA = 4πr2, which in this case becomes SA = 4πx2, where x is the radius of the sphere. |
Surface Area |
|
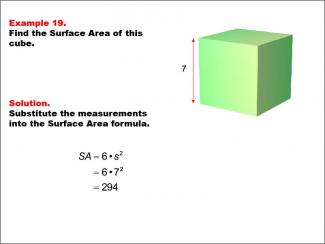
Math Example--Area and Perimeter--Surface Area: Example 19 |
Math Example--Area and Perimeter--Surface Area: Example 19TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cube with a side length of 7 units. The surface area is calculated using the formula SA = 6s2, where s is the length of one side of the cube. For this specific cube, the calculation yields a surface area of 294 square units. |
Surface Area |
|
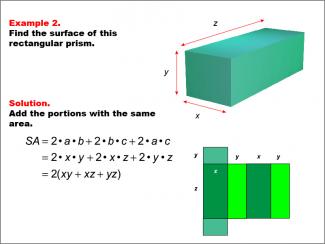
Math Example--Area and Perimeter--Surface Area: Example 2 |
Math Example--Area and Perimeter--Surface Area: Example 2TopicSurface Area DescriptionThis example introduces a general formula for calculating the surface area of a rectangular prism with dimensions x, y, and z. The surface area is computed using the formula SA = 2xy + 2xz + 2yz, which can be simplified to 2(xy + xz + yz). This generalized approach allows for easy application to prisms of various sizes. Surface area calculations are fundamental in mathematics, with applications ranging from manufacturing to environmental science. This collection of examples aids in teaching the topic by presenting both specific and general cases, helping students understand how to apply formulas flexibly to different scenarios. |
Surface Area |
|
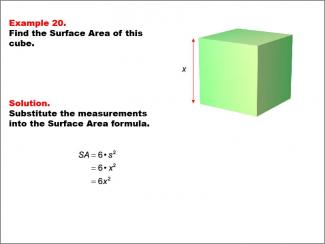
Math Example--Area and Perimeter--Surface Area: Example 20 |
Math Example--Area and Perimeter--Surface Area: Example 20TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cube with an unknown side length labeled as "x". The surface area is calculated using the formula SA = 6s2, which in this case becomes SA = 6x2, where x is the length of one side of the cube. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 21 |
Math Example--Area and Perimeter--Surface Area: Example 21TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cube with an outer side length of 9 units and an inner hollow square side length of 7 units. The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 is the outer side length and s2 is the inner side length. For this specific hollow cube, the calculation yields a surface area of 388 square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 22 |
Math Example--Area and Perimeter--Surface Area: Example 22TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cube with variable dimensions. The outer side length is labeled as "x" and the inner hollow side length as "x - 2". The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 = x and s2 = x - 2. After expanding and simplifying, the result is SA = 4(x2 + 2x - 2) square units. |
Surface Area |
|
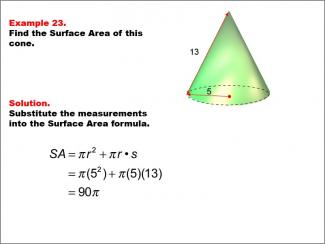
Math Example--Area and Perimeter--Surface Area: Example 23 |
Math Example--Area and Perimeter--Surface Area: Example 23TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cone with a radius of 5 units and a slant height of 13 units. The surface area is calculated using the formula SA = π * r2 + π * r * s, where r is the radius and s is the slant height. For this specific cone, the calculation yields a surface area of 90π square units. |
Surface Area |
|
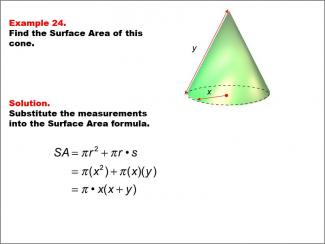
Math Example--Area and Perimeter--Surface Area: Example 24 |
Math Example--Area and Perimeter--Surface Area: Example 24TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cone with variable dimensions. The radius is labeled as "x" and the slant height as "y". The surface area is calculated using the formula SA = π * r2 + π * r * s, where r = x and s = y. This simplifies to SA = π * x(x + y) square units. |
Surface Area |
|
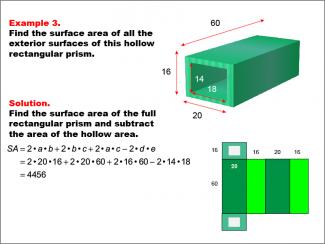
Math Example--Area and Perimeter--Surface Area: Example 3 |
Math Example--Area and Perimeter--Surface Area: Example 3TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow rectangular prism. The outer dimensions are 60, 20, and 16 units, while the inner dimensions are 18 and 14 units. The surface area is determined by subtracting the area of the hollow region from the surface area of the full rectangular prism, resulting in a surface area of 4456 square units. |
Surface Area |
|
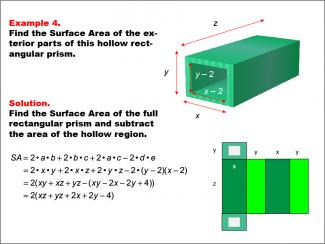
Math Example--Area and Perimeter--Surface Area: Example 4 |
Math Example--Area and Perimeter--Surface Area: Example 4TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow rectangular prism. The outer dimensions are represented by x, y, and z, while the hollow dimensions are represented by (y - 2) and (x - 2). The surface area is determined by subtracting the hollow region's surface area from that of the full rectangular prism, resulting in the formula SA = 2(xz + yz + 2x + 2y - 4). |
Surface Area |
|
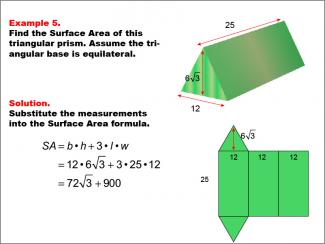
Math Example--Area and Perimeter--Surface Area: Example 5 |
Math Example--Area and Perimeter--Surface Area: Example 5TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a triangular prism with an equilateral triangular base. The base is 12 units, the height is 6 * √(3), and the length of the prism is 25 units. The surface area is calculated using the formula SA = b * h + 3 * l * w, where b is the base, h is the height of the triangle, l is the length of the prism, and w is the width of the triangle. The final result is 72 * √(3) + 900 square units. |
Surface Area |
|
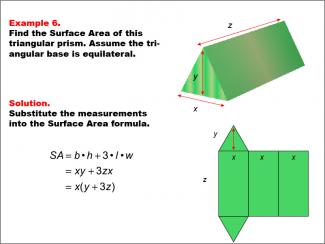
Math Example--Area and Perimeter--Surface Area: Example 6 |
Math Example--Area and Perimeter--Surface Area: Example 6TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a triangular prism with an equilateral triangular base. The dimensions are represented by x for the base, y for the height of the triangle, and z for the length of the prism. The surface area is determined using the formula SA = b * h + 3 * l * w, which simplifies to SA = xy + 3zx = x(y + 3z). |
Surface Area |
|
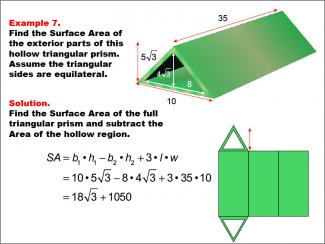
Math Example--Area and Perimeter--Surface Area: Example 7 |
Math Example--Area and Perimeter--Surface Area: Example 7TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow triangular prism with an equilateral triangular base. The outer triangle has a base of 10 units and a height of 5 * √(3), while the inner triangle has a base of 8 units and a height of 4 * √(3). The length of the prism is 35 units. The surface area is calculated by subtracting the area of the hollow region from the full prism's surface area, resulting in SA = b1 * h1 - b2 * h2 + 3 * l * w = (18 * √(3)) + 1050 square units. |
Surface Area |
|
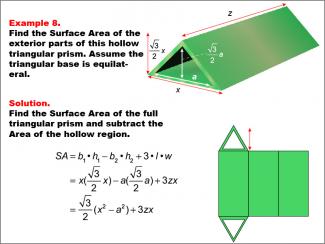
Math Example--Area and Perimeter--Surface Area: Example 8 |
Math Example--Area and Perimeter--Surface Area: Example 8TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow triangular prism with an equilateral triangular base. The outer triangle has a base labeled as x, and the inner triangle has a base labeled as a. The heights are given as √(3)/2 for both triangles, and the length of the prism is z units. The surface area is determined by subtracting the area of the hollow region from the full prism's surface area, resulting in the formula SA = (√(3)/2) (x2 - a2) + 3zx. |
Surface Area |
|
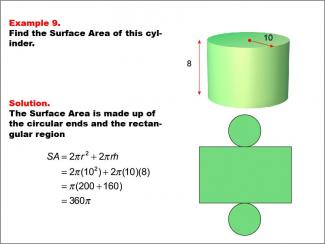
Math Example--Area and Perimeter--Surface Area: Example 9 |
Math Example--Area and Perimeter--Surface Area: Example 9TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cylinder with a radius of 10 units and a height of 8 units. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, where r is the radius and h is the height. For this specific cylinder, the calculation yields a surface area of 360π square units. |
Surface Area |

|
MATH EXAMPLES--Teacher's Guide: Surface Area |
MATH EXAMPLES--Teacher's Guide: Surface Area
This Teacher's Guide provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Math in the News: Issue 35--125 and Counting |
Math in the News: Issue 35--125 and Counting
11/14/11. In this issue we commemorate the 125th anniversary of the Statue of Liberty. We also look at the geometry and architecture of this monument. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area and Volume |