
Illustrative Math Alignment: Grade 6 Unit 2
Introducing Ratios
Lesson 10:Comparing Situations by Examining Ratios
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Definitions Collection: Ratios, Proportions, and Percents |
OverviewThis collection of definitions on the topic of Ratios, Proportions, and Percents from Media4Math is an invaluable educational resource designed to enhance students' understanding of these fundamental mathematical concepts. This comprehensive collection includes essential terms such as ratio, proportion, percent, rate, unit rate, and scale model. |
Applications of Ratios, Proportions, and Percents, Ratios and Rates, Percents and Proportions |

|
Definition--Measures of Central Tendency--Average Speed |
Average SpeedTopicStatistics DefinitionAverage speed is the total distance traveled divided by the total time taken. DescriptionThis concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations. |
Data Analysis |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units |
Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios |
Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios |
Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios |
Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate |
RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio |
RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions |
Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |
|
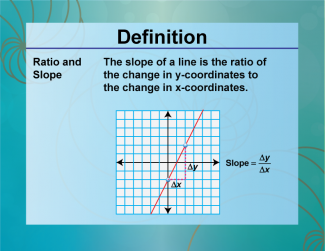
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope |
Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals |
Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions |
Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents |
Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--The Golden Ratio |
The Golden RatioTopicRatios, Proportions, and Percents DefinitionThe Golden Ratio is a special number approximately equal to 1.618, often denoted by the Greek letter φ (phi), which appears in various aspects of art, architecture, and nature. |
Applications of Ratios, Proportions, and Percents and Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Unit Rate |
Unit RateTopicRatios, Proportions, and Percents DefinitionA unit rate is a comparison of any two separate but related measurements when one of the measurements is reduced to a single unit. DescriptionUnit rates are commonly used in everyday life, such as calculating speed (miles per hour), cost per item, or efficiency (miles per gallon). For example, if a car travels 300 miles on 10 gallons of gas, the unit rate is 30 miles per gallon. |
Ratios and Rates |
|
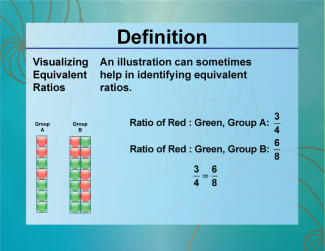
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Equivalent Ratios |
Visualizing Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionVisualizing equivalent ratios involves using diagrams or models to show that two ratios are equivalent. DescriptionVisualizing equivalent ratios is important in fields such as mathematics and engineering, where understanding proportional relationships is crucial. For example, using a double number line or a ratio table can help illustrate that the ratios 2:3 and 4:6 are equivalent. |
Ratios and Rates |
|
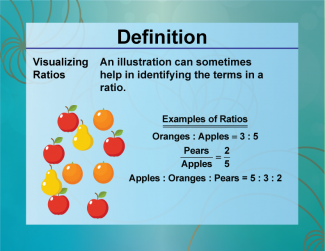
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Ratios |
Visualizing RatiosTopicRatios, Proportions, and Percents DefinitionVisualizing ratios involves using diagrams or models to represent and understand the relationship between two quantities. DescriptionVisualizing ratios is essential in various fields, such as mathematics, science, and economics, where understanding the relationship between quantities is crucial. For example, using a bar model or a double number line can help illustrate the ratio of 3:4. |
Ratios and Rates |

|
Instructional Resource: Applications of Linear Functions: Speed and acceleration |
In this Slide Show, apply concepts of linear functions to the context of speed and acceleration. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 01 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 01TopicQuadratics DescriptionThis image features a vintage car in motion with a blurred background, emphasizing speed. It serves as an introduction to the series on speed and acceleration in linear and quadratic functions. The image visually represents the concept of speed through motion blur, making it relatable for students learning about linear functions. By using this image, teachers can engage students with real-world applications of mathematical concepts. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
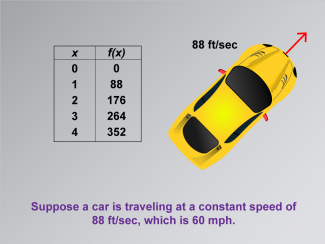
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 02 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 02TopicQuadratics DescriptionThis image depicts a yellow car alongside a table that shows time in seconds and distance in feet, illustrating a constant speed of 88 ft/sec (60 mph). The table provides a clear example of how linear functions can represent constant speeds. Teachers can use this image to demonstrate the relationship between time, distance, and speed, reinforcing the concept of constant rates within linear functions. |
Graphs of Linear Functions and Graphs of Quadratic Functions |

|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 03 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 03TopicQuadratics DescriptionThis image is a variation of the previous image that highlights the common difference as the rate of speed. It builds on the previous example by emphasizing how the common difference (88 ft/sec) serves as the rate in linear equations. This visual representation helps students grasp how mathematical differences translate into real-world speeds. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
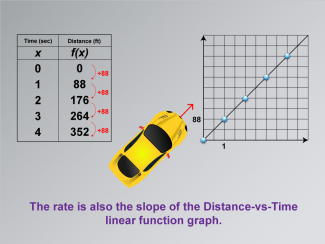
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 04 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 04TopicQuadratics DescriptionThis image presents a table with time in seconds and distance in feet, accompanied by a graph illustrating a linear relationship between time and distance. The constant increase of 88 feet per second is depicted as the slope of the Distance-vs-Time linear function graph. This visual aids students in understanding how linear functions can model real-world speed scenarios. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
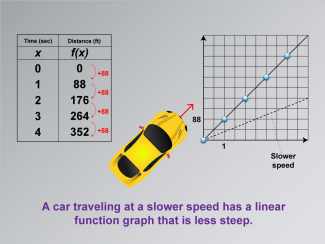
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 05 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 05TopicQuadratics DescriptionThis image is a variation showing time and distance data with a graph that includes a dotted line labeled "Slower speed." The graph illustrates how different speeds affect the steepness of linear function graphs. This visual comparison helps students see how speed variations are represented mathematically. Using math clip art allows students to visualize differences in speed through graphical representations, aiding comprehension of linear functions' applications. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
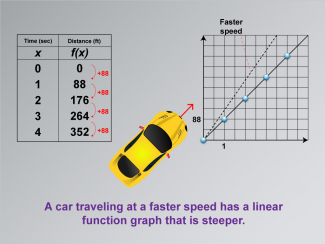
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 06 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 06TopicQuadratics DescriptionThis image shows a graph similar to the previous one but with a steeper dotted line labeled "Faster speed." It visually demonstrates how increased speed results in a steeper slope on a linear function graph. This helps students understand the relationship between speed changes and their graphical representations. The use of math clip art facilitates learning by providing clear visual examples that connect mathematical concepts to real-world scenarios. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
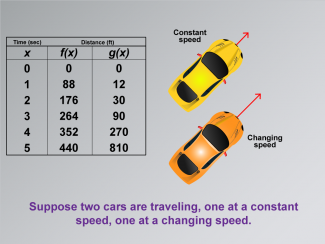
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 07 |
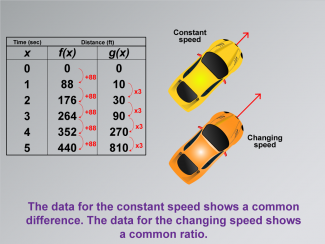
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 07TopicQuadratics DescriptionThis image displays a table with time and distance data for two functions, f(x) representing constant speed, and g(x) representing changing speed. Two car icons illustrate these concepts visually. This comparison allows students to explore how different types of motion are modeled mathematically. The use of math clip art aids in understanding complex concepts by providing relatable visual examples that highlight differences in mathematical functions. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 08 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 08TopicQuadratics DescriptionThis image presents time-distance data for functions f(x) with constant increments, showing constant speed, while g(x) shows changing speed with a common ratio. The visual representation helps students understand different mathematical relationships through real-world examples. The use of math clip art enhances comprehension by clearly illustrating abstract concepts like common differences versus common ratios in mathematical functions. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
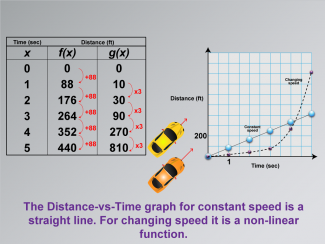
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 09 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 09TopicQuadratics DescriptionThis image features a graph comparing linear and non-linear functions, illustrating constant and changing speeds. The visual contrast between the two types of functions helps students understand how different speeds are modeled mathematically. The linear function represents constant speed, while the non-linear function shows acceleration or deceleration. Math clip art like this is crucial for teaching because it provides visual clarity, helping students differentiate between linear and quadratic functions in real-world contexts. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
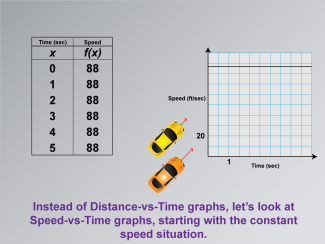
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 10 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 10TopicQuadratics DescriptionThis image illustrates a constant speed through a graph that shows a straight line, representing uniform motion. It provides an opportunity for students to see how consistent motion is represented visually in a linear function. The consistent slope indicates constant speed, making it easier for students to connect mathematical concepts with practical applications. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
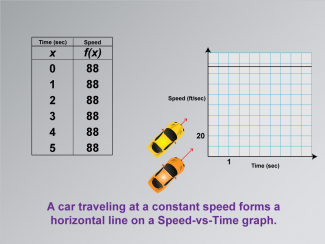
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 11 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 11TopicQuadratics DescriptionThis image shows a graph and data for a constant speed scenario. The graph helps students understand how different speeds are represented in mathematical models, with linear sections indicating constant speed and curved sections showing acceleration or deceleration. Math clip art like this is essential for teaching as it visually differentiates between linear and quadratic functions, providing clarity in understanding real-world applications. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 12 |
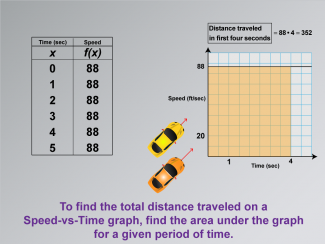
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 12TopicQuadratics DescriptionThis image includes a Speed-vs-Time graph with an area under the curve highlighted to represent distance traveled over time. The calculation for distance (88 * 4 = 352) is shown, helping students visualize how to determine total distance using graphs. The use of math clip art enhances learning by providing visual context for abstract concepts like integration in real-world scenarios. Teacher's Script: "See the shaded area? It represents distance. How do we calculate it? Let's find out." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 13 |
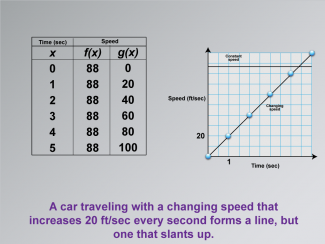
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 13TopicQuadratics DescriptionThis image shows a graph displaying two lines: a horizontal line for constant speed and a slanted line for changing speed. It illustrates how different speeds are represented graphically, helping students understand the concept of acceleration. The use of math clip art provides clarity by visually differentiating between constant and changing speeds, aiding comprehension. Teacher's Script: "Look at these lines. How do they show different speeds? Let's explore what these shapes tell us." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 14 |
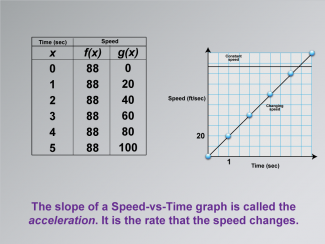
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 14TopicQuadratics DescriptionThis image includes a table with time (x) and speed (f(x) and g(x)). The graph shows constant and changing speeds, emphasizing the slope. The slope of a Speed-vs-Time graph is called acceleration, which is the rate that speed changes. The use of math clip art helps students visualize how acceleration is represented graphically, aiding in understanding real-world applications. Teacher's Script: "Notice the slope of these lines. How does it show acceleration? Let's explore what this means for speed changes." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 15 |
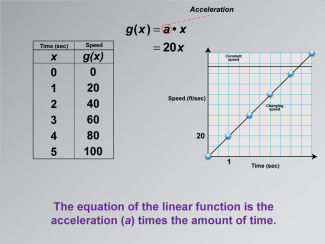
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 15TopicQuadratics DescriptionThis image presents a table with time (x) and speed (g(x)). The graph emphasizes acceleration as the slope, with an equation showing g(x) = 20x. The equation of the linear function is the acceleration (a) times the amount of time. The use of math clip art clarifies how equations relate to real-world motion, enhancing comprehension. Teacher's Script: "See how the equation shows acceleration? What does the slope tell us about speed changes?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
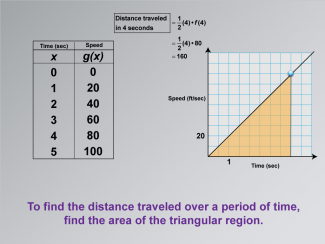
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 16 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 16TopicQuadratics DescriptionThis image features a table with time versus speed data, along with a graph that explains finding distance by calculating the area under a triangular region. To find the distance traveled over a period, calculate the area of the triangular region. The use of math clip art aids in understanding by connecting theoretical concepts with practical applications. Teacher's Script: "Notice how we find distance using the triangle area. How does this connect to what we've learned about motion?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |

|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 17 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 17TopicQuadratics DescriptionThis image displays a graph with speed versus time, highlighting the equation of the line and the area under it. It emphasizes using these equations when acceleration starts from zero. If you know the acceleration rate of a car that starts from speed zero, use these equations for speed and distance traveled. The use of math clip art provides visual clarity in understanding how equations model motion from rest. Teacher's Script: "Notice these equations—how do they help us understand acceleration from rest?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
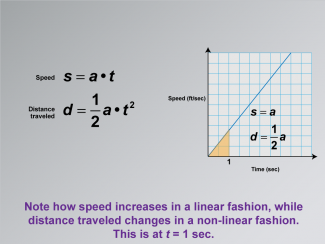
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 18 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 18TopicQuadratics DescriptionThis image shows a graph with speed on the y-axis and time on the x-axis. The equations for speed and distance traveled are given as s = a⋅t and d = 1/2at2. The graph illustrates how speed increases linearly, while distance traveled follows a non-linear path. Math clip art like this helps students understand the difference between linear and quadratic relationships in real-world contexts. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
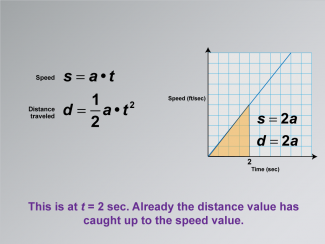
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 19 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 19TopicQuadratics DescriptionThis image shows a graph similar to the previous image but at t = 2 seconds. The equations are updated to s = 2a and d = 2a, indicating that distance has caught up with speed. The use of math clip art provides visual clarity in understanding dynamic interactions between speed and distance over time. Teacher's Script: "At two seconds, notice how distance catches up to speed. What does this mean for our understanding of motion?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
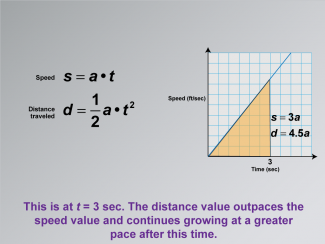
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 20 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 20TopicQuadratics DescriptionThis image depicts a graph of speed versus time with no initial velocity. The equations shown are s = a⋅t for speed and d = 1/2at2 for distance traveled. At t = 3 seconds, the graph highlights that distance outpaces speed. The use of math clip art helps students visualize how distance can grow faster than speed under certain conditions. Teacher's Script: "At three seconds, see how distance outpaces speed? Let's explore why this happens." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
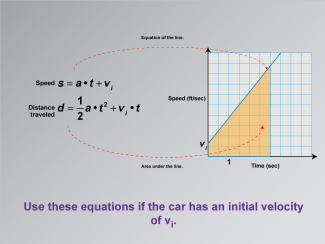
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 21 |
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 21TopicQuadratics DescriptionThis image shows a graph with a line representing speed as a function of time, with initial velocity. The equations for speed are s = a⋅t+vi and for distance traveled are d= 1/2at2 +vi •t. The graph illustrates the area under the line, indicating distance. The use of math clip art provides students with visual tools to understand how initial velocity affects motion over time. Teacher's Script: "Notice how initial velocity changes the graph. How does this affect our calculations for distance?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |

|
Math in the News: Issue 95--The Iditarod Race |
Math in the News: Issue 95--The Iditarod Race
March 2014. In this issue of Math in the News we look at the Iditarod Race in Alaska. This gives us an opportunity to analyze data on average speed. We look at data in tables and line graphs and analyze the winning speeds over the history of the race. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Video Transcript: Algebra Nspirations: Linear Functions, 1 |
Video Transcript: Algebra Nspirations: Linear Functions, Part 1
This is the transcript for the video of same title. Video contents: In this Investigation we look at linear models for objects moving at a constant speed. This is part of a collection of video transcript from the Algebra Nspirations video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Tutorial: Ratios, Video 1 |
Video Tutorial: Ratios, Video 1
TopicRatios DescriptionThis video introduces the concept of ratios, which describe relationships between quantities. Key concepts include writing ratios in different forms (e.g., 2:3, 2/3, and 2 to 3) and simplifying ratios. It also covers part-to-part ratios and part-to-whole ratios using examples like sports balls and colored shapes. Applications include categorizing objects and exploring numerical relationships in sets. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 11 |
Video Tutorial: Ratios, Video 11
TopicRatios DescriptionThis video focuses on solving proportions algebraically, converting them into equations to solve real-world problems. Examples include predator-prey ratios, scaling pizza dough recipes, and creating shades of paint. The video demonstrates methods for handling terms in denominators and simplifying ratios to whole numbers. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 12 |
Video Tutorial: Ratios, Video 12
TopicRatios DescriptionThe video explains how proportions are used to create scale drawings, ensuring geometric figures remain proportional. Examples include finding dimensions in similar triangles, scaling architectural models, and solving geometric problems. The concept of proportional relationships is key to accurate scaling. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 13 |
Video Tutorial: Ratios, Video 13
TopicRatios DescriptionThis video demonstrates calculating rates from data sets, focusing on patterns like distance-time relationships and wages. Examples include determining car speeds, hourly wages, and unit costs of gasoline. Data tables are used to visualize and compute rates. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 14 |
Video Tutorial: Ratios, Video 14
TopicRatios DescriptionRates are linked to slopes in linear functions. The video explores calculating rates of change for graphs of speed, savings growth, and loan repayment. It highlights using the slope formula to interpret and solve practical problems. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 15 |
Video Tutorial: Ratios, Video 15
TopicRatios DescriptionThis video covers converting units using rates, with examples like speed conversion, currency exchange, and calculating seconds in a year. It emphasizes multiplication by conversion rates to transition between units effectively. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 16 |
Video Tutorial: Ratios, Video 16
TopicRatios DescriptionRatios are connected to percentages in this video. Examples include finding percentages of items in collections. It develops a formula for converting part-to-whole ratios into percentages. Relevance to the Topic: This video is a crucial resource for understanding the concept of Ratios. It delves into mathematical foundations by exploring how ratios function in real-life scenarios, such as scaling, comparisons, or visual representations. The mathematical principles demonstrated include proportional reasoning, equivalence, and fraction comparisons. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 17 |
Video Tutorial: Ratios, Video 17
TopicRatios DescriptionThis video illustrates converting ratios to percents using visual aids like area models and grids. Examples include determining percentages of colored eggs, fruit types, and combinations of colored lights. |
Ratios and Rates |

|
Video Tutorial: Ratios, Video 18 |
Video Tutorial: Ratios, Video 18
TopicRatios DescriptionThe video explores working with ratios involving decimals, such as finding unit costs or recycling rates. Scientific notation and multi-step conversions are used to calculate speeds of spacecraft like Voyager I. |
Ratios and Rates |