Illustrative Math Alignment: Grade 6 Unit 3

Unit Rates and Percentages

Lesson 7: Equivalent Ratios Have the Same Unit Rates

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
Closed Captioned Video: Algebra Applications: Inequalities, 1	Closed Captioned Video: Algebra Applications: Inequalities, 2 Topic Inequalities Description This video models an inequality to explain how floodgates in Venice prevent flooding during storms. The key concept is the activation threshold, where the water level exceeds a critical value. Vocabulary includes inequality, threshold, variable, and model. Using a TI-Nspire, the video demonstrates creating a random variable for water levels and a function to evaluate if floodgates should activate. It illustrates real-world applications in engineering and environmental management.	Applications of Equations and Inequalities and Inequalities
Closed Captioned Video: Ratios and Rates: Converting Measurement Units	Closed Captioned Video: Ratios and Rates: Converting Measurement Units Topic Ratios Description This video covers converting units using rates, with examples like speed conversion, currency exchange, and calculating seconds in a year. It emphasizes multiplication by conversion rates to transition between units effectively.	Ratios and Rates
Closed Captioned Video: Ratios and Rates: Rates and Slopes of Lines	Closed Captioned Video: Ratios and Rates: Rates and Slopes of Lines Topic Ratios Description Rates are linked to slopes in linear functions. The video explores calculating rates of change for graphs of speed, savings growth, and loan repayment. It highlights using the slope formula to interpret and solve practical problems.	Ratios and Rates
Closed Captioned Video: Ratios and Rates: Rates from Data	Closed Captioned Video: Ratios and Rates: Rates from Data Topic Ratios Description This video demonstrates calculating rates from data sets, focusing on patterns like distance-time relationships and wages. Examples include determining car speeds, hourly wages, and unit costs of gasoline. Data tables are used to visualize and compute rates.	Ratios and Rates
Closed Captioned Video: Ratios and Rates: Ratios as Decimals	Closed Captioned Video: Ratios and Rates: Ratios as Decimals Topic Ratios Description The video explores working with ratios involving decimals, such as finding unit costs for salmon or recycling rates. Scientific notation and multi-step conversions are used to calculate speeds of spacecraft like Voyager I.	Ratios and Rates
Closed Captioned Video: Ratios, Proportions, and Percents: Calculating Percents	Closed Captioned Video: Ratios, Proportions, and Percents: Calculating Percents Topic Ratios Description Ratios are connected to percentages in this video. Examples include finding percentages of colored socks or non-green items in collections. It develops a formula for converting part-to-whole ratios into percentages.	Ratios and Rates
Closed Captioned Video: Ratios: Equivalent Ratios	Closed Captioned Video: Ratios: Equivalent Ratios Topic Ratios Description This video explains generating and comparing equivalent ratios. Examples include simplifying fractions, determining similarity in geometric shapes, and integrating multiple ratios into a comprehensive ratio. Applications extend to geometry and proportional reasoning.	Ratios and Rates
Closed Captioned Video: Ratios: Rates	Closed Captioned Video: Ratios: Rates Topic Ratios Description This video introduces rates, a type of ratio comparing different units, such as distance over time (speed) or dollars per hour (wage). Examples demonstrate calculating rates and converting units. Applications include measuring efficiency and performing unit conversions.	Ratios and Rates
Closed Captioned Video: Ratios: Unit Rates	Closed Captioned Video: Ratios: Unit Rates Topic Ratios Description The video focuses on unit rates, where the denominator equals one. It includes practical examples like finding the cost per pound of bananas or determining hourly wages. Applications extend to conversions and scaling calculations for various real-world tasks.	Ratios and Rates
Closed Captioned Video: Ratios: Visual Models for Ratios and Percents	Closed Captioned Video: Ratios: Visual Models for Ratios and Percents Topic Ratios Description This video illustrates converting ratios to percents using visual aids like area models and grids. Examples include determining percentages of colored eggs, fruit types, and combinations of colored lights.	Ratios and Rates
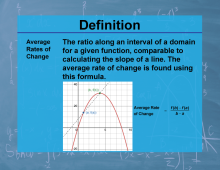
Definition--Calculus Topics--Average Rates of Change	Definition--Calculus Topics--Average Rates of Change Topic Calculus Definition The average rate of change of a function over an interval is the slope of the secant line connecting the endpoints of that interval on the function's graph. Description The average rate of change is a fundamental concept in calculus that bridges the gap between algebra and calculus. It provides insight into how a function's output changes relative to its input over a specific interval. This concept is crucial in various real-world applications, such as calculating average speed, growth rates, or productivity changes.	Calculus Vocabulary
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax	Calculating Tax Topic Ratios, Proportions, and Percents Definition Calculating tax involves determining the percentage amount to be added to the base price of a product or service. Description Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is	Applications of Ratios, Proportions, and Percents
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tips	Calculating Tips Topic Ratios, Proportions, and Percents Definition Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill. Description Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 80 × 0.15 = 12	Applications of Ratios, Proportions, and Percents
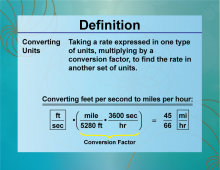
Definition--Ratios, Proportions, and Percents Concepts--Converting Units	Converting Units Topic Ratios, Proportions, and Percents Definition Converting units involves changing a measurement from one unit to another using a conversion factor. Description Converting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis	Dimensional Analysis Topic Ratios, Proportions, and Percents Definition Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors. Description Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds:	Applications of Ratios, Proportions, and Percents
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios	Equivalent Ratios Topic Ratios, Proportions, and Percents Definition Equivalent ratios are ratios that express the same relationship between quantities. Description Equivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios	Part-to-Part Ratios Topic Ratios, Proportions, and Percents Definition Part-to-part ratios compare different parts of a whole to each other. Description Part-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios	Part-to-Whole Ratios Topic Ratios, Proportions, and Percents Definition Part-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. Description Part-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Percent	Percent Topic Ratios, Proportions, and Percents Definition A percent is a ratio that compares a number to 100. Description Percentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90%	Percents
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease	Percent Decrease Topic Ratios, Proportions, and Percents Definition Percent decrease measures the reduction in value expressed as a percentage of the original value. Description Percent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%.	Percents
Definition--Ratios, Proportions, and Percents Concepts--Percent Increase	Percent Increase Topic Ratios, Proportions, and Percents Definition Percent increase measures the growth in value expressed as a percentage of the original value. Description Percent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth. For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as (75 − 50)/50 × 100 = 50%	Percents
Definition--Ratios, Proportions, and Percents Concepts--Percent of a Number	Percent of a Number Topic Ratios, Proportions, and Percents Definition Percent of a number involves calculating the amount represented by a certain percentage of that number. Description Understanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping.	Percents
Definition--Ratios, Proportions, and Percents Concepts--Percent of an Unknown	Percent of an Unknown Topic Ratios, Proportions, and Percents Definition Percent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity. Description Knowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount. For instance, if 20% of an unknown number equals 15, you can set up the equation: 0.20x = 15	Percents
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals	Percents as Decimals Topic Ratios, Proportions, and Percents Definition Percents as decimals involve converting a percentage into its decimal representation. Description Converting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy.	Percents
Definition--Ratios, Proportions, and Percents Concepts--Proportion	Proportion Topic Ratios, Proportions, and Percents Definition A proportion is an equation that states that two ratios are equal. Description Understanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio.	Proportions
Definition--Ratios, Proportions, and Percents Concepts--Proportional	Proportional Topic Ratios, Proportions, and Percents Definition Proportional refers to the relationship between two quantities where their ratio is constant. Description Proportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations.	Proportions
Definition--Ratios, Proportions, and Percents Concepts--Rate	Rate Topic Ratios, Proportions, and Percents Definition A rate is a ratio that compares two quantities with different units. Description Rates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratio	Ratio Topic Ratios, Proportions, and Percents Definition A ratio is a comparison of two quantities by division. Description Ratios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions	Ratios and Fractions Topic Ratios, Proportions, and Percents Definition Ratios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. Description Understanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio.	Ratios and Rates
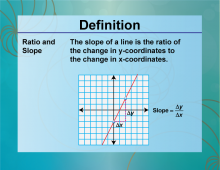
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope	Ratios and Slope Topic Ratios, Proportions, and Percents Definition The slope of a line is a ratio that represents the change in y over the change in x. Description Understanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form	Ratios in Simplest Form Topic Ratios, Proportions, and Percents Definition Ratios in simplest form are ratios that have been reduced to their smallest whole number terms. Description Reducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities.	Applications of Ratios, Proportions, and Percents
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals	Ratios with Decimals Topic Ratios, Proportions, and Percents Definition Ratios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. Description Ratios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions	Ratios with Fractions Topic Ratios, Proportions, and Percents Definition Ratios with fractions compare two quantities where one or both of the quantities are fractions. Description Ratios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents	Ratios with Percents Topic Ratios, Proportions, and Percents Definition Ratios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. Description Ratios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis.	Ratios and Rates
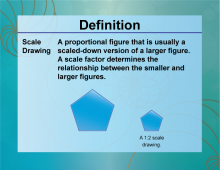
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing	Scale Drawing Topic Ratios, Proportions, and Percents Definition A scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. Description Scale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model.	Proportions
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor	Scale Factor Topic Ratios, Proportions, and Percents Definition A scale factor is a number that scales, or multiplies, some quantity. Description Scale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering.	Proportions
Definition--Ratios, Proportions, and Percents Concepts--Similar Figures	Similar Figures Topic Ratios, Proportions, and Percents Definition Similar figures are figures that have the same shape but may differ in size; their corresponding angles are equal, and their corresponding sides are proportional. Description Similar figures are fundamental in geometry and are used in various real-world applications, such as creating scale models and maps. For example, two triangles are similar if their corresponding angles are equal and their sides are in proportion. This concept is essential for understanding geometric relationships and solving problems involving shapes and sizes.	Proportions
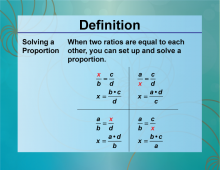
Definition--Ratios, Proportions, and Percents Concepts--Solving Proportions	Solving Proportions Topic Ratios, Proportions, and Percents Definition Solving proportions involves finding the value of a variable that makes two ratios equal. Description Solving proportions is a key skill in algebra and is used in various applications, such as scaling recipes, converting units, and solving real-world problems. For example, if you know that 2/3 = x/6 you can solve for x by cross-multiplying to get 2 * 6 = 3 * x leading to x = 4	Proportions
Definition--Ratios, Proportions, and Percents Concepts--The Constant of Proportionality	The Constant of Proportionality Topic Ratios, Proportions, and Percents Definition The constant of proportionality is the constant value that relates two proportional quantities. Description The constant of proportionality is a fundamental concept in mathematics, particularly in linear relationships and direct variation. For example, in the equation y = kx, k is the constant of proportionality that relates y and x. This concept is crucial in fields like physics, where it is used to describe relationships such as speed (distance/time).	Proportions
Definition--Ratios, Proportions, and Percents Concepts--The Golden Ratio	The Golden Ratio Topic Ratios, Proportions, and Percents Definition The Golden Ratio is a special number approximately equal to 1.618, often denoted by the Greek letter φ (phi), which appears in various aspects of art, architecture, and nature.	Applications of Ratios, Proportions, and Percents and Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--The Percent One Number Is of Another	The Percent One Number Is of Another Topic Ratios, Proportions, and Percents Definition The percent one number is of another is a way to express one number as a percentage of another number. Description Understanding how to express one number as a percentage of another is crucial in various real-world applications, such as calculating discounts, tax, and interest rates. For example, if you want to find out what percentage 25 is of 200, you divide 25 by 200 and multiply by 100, resulting in 12.5%.	Percents
Definition--Ratios, Proportions, and Percents Concepts--Unit Rate	Unit Rate Topic Ratios, Proportions, and Percents Definition A unit rate is a comparison of any two separate but related measurements when one of the measurements is reduced to a single unit. Description Unit rates are commonly used in everyday life, such as calculating speed (miles per hour), cost per item, or efficiency (miles per gallon). For example, if a car travels 300 miles on 10 gallons of gas, the unit rate is 30 miles per gallon.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Visual Models for Percents	Visual Models for Percents Topic Ratios, Proportions, and Percents Definition Visual models for percents are diagrams or illustrations that represent percentages to help visualize and understand them. Description Visual models for percents are useful tools in various fields, such as education, finance, and statistics, to represent data and make it more comprehensible. For example, pie charts and bar graphs are common visual models that help illustrate percentages and proportions effectively.	Percents
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Equivalent Ratios	Visualizing Equivalent Ratios Topic Ratios, Proportions, and Percents Definition Visualizing equivalent ratios involves using diagrams or models to show that two ratios are equivalent. Description Visualizing equivalent ratios is important in fields such as mathematics and engineering, where understanding proportional relationships is crucial. For example, using a double number line or a ratio table can help illustrate that the ratios 2:3 and 4:6 are equivalent.	Ratios and Rates
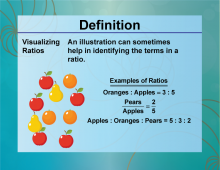
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Ratios	Visualizing Ratios Topic Ratios, Proportions, and Percents Definition Visualizing ratios involves using diagrams or models to represent and understand the relationship between two quantities. Description Visualizing ratios is essential in various fields, such as mathematics, science, and economics, where understanding the relationship between quantities is crucial. For example, using a bar model or a double number line can help illustrate the ratio of 3:4.	Ratios and Rates
Desmos Activity: Slope As Rate of Change	Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost.	Slope and Ratios and Rates
INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Wildfires So Dangerous?	INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Wildfires So Dangerous? In this Algebra Application, students learn about wildfires and the measurement of air quality. The math topics covered include: Scientific notation, Rates, Density, Data Analysis. The specific focus of this investigation is the health hazards from wildfire smoke. This includes a discussion of air density, measurement in microns, and measurement of air quality. Links to various web sites, including the EPA's site, provide relevant background information and data. The culminating activity is a case study of the wildfires in the Lake Tahoe area. Students analyze historical data and make a recommendation on the air quality. This is a great back-to-school activity for middle school or high school students. A relevant real-world application allows them to review math concepts.	Laws of Exponents and Applications of Ratios, Proportions, and Percents
Math Clip Art--Applications of Equivalent Ratios--Vehicle Ratios 1	Math Clip Art--Applications of Equivalent Ratios--Vehicle Ratios 1 Topic Ratios Description This math clip art image is a title card for a series of math clip art images that apply equivalent ratios problems. The subsequent images show different vehicle ratios. This image, along with the overall collection, can be used to teach ratios by comparing the number of cars to other vehicle types or parking spaces. Teachers can use this visual to introduce the concept of part-to-whole ratios, such as the ratio of cars to total vehicles, or part-to-part ratios, like comparing the number of cars to motorcycles or SUVs in subsequent images.	Ratios and Rates
Math Clip Art--Applications of Equivalent Ratios--Vehicle Ratios 10	Math Clip Art--Applications of Equivalent Ratios--Vehicle Ratios 10 Topic Ratios Description This math clip art image displays a table with two rows labeled "Motorcycles" and "SUVs". The numbers in the table are 1, 2, 3, 4, 5 for Motorcycles and 2, 4, 6, 8, 10 for SUVs. This visual representation is crucial for teaching the concept of equivalent ratios using a different set of vehicles.	Ratios and Rates
Math Clip Art--Applications of Equivalent Ratios--Vehicle Ratios 2	Math Clip Art--Applications of Equivalent Ratios--Vehicle Ratios 2 Topic Ratios Description This math clip art image showcases a red car in a parking garage with numbered pillars in the background. The caption "40 Cars" provides context for the ratio concept being illustrated. This image is part of a series designed to teach equivalent ratios using vehicles as a relatable subject matter.	Ratios and Rates