Illustrative Math Alignment: Grade 6 Unit 1

Overview

The Equations collection on Media4Math is an invaluable resource for students and educators alike, offering a comprehensive set of definitions related to equations. This collection includes essential terms such as linear equations, quadratic equations, and polynomial equations. Each term is clearly defined, providing students with a solid foundation in understanding the various types of equations they will encounter in their studies.

Overview

Overview

Overview

Topic

Equations

Ever since the mathematics of the Babylonians, equations have played a central role in the development of algebra. Written and hosted by internationally acclaimed mathematics educator Dr. Monica Neagoy, this video traces the history and evolution of equations. It explores the two principal equations encountered in an introductory algebra course--linear and quadratic--in an engaging way. The foundations of algebra are explored and fundamental questions about the nature of algebra are answered. In addition, problems involving linear and quadratic equations are solved using the TI-Nspire graphing calculator. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series.

In this episode of Algebra Applications, two real-world explorations are developed: Biology. Analyzing statistics from honey bee production allows for a mathematical analysis of the so-called Colony Collapse Disorder. Geology. Why do rivers meander instead of traveling in a straight line? In this segment the geological forces that account for a river’s motion are explained.

An overview of the key topics to be covered in the video.

Honey bees not only produce a tasty treat, they also help pollinate flowering plants that provide much of the food throughout the world. So, when in 2006 bee colonies started dying out, scientists recognized a serious problem. Analyzing statistics from honey bee production allows for a mathematical analysis of the so-called Colony Collapse Disorder.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Ever since the mathematics of the Babylonians, equations have played a central role in the development of algebra. Written and hosted by internationally acclaimed mathematics educator Dr. Monica Neagoy, this video traces the history and evolution of equations. It explores the two principal equations encountered in an introductory algebra course--linear and quadratic--in an engaging way. The foundations of algebra are explored and fundamental questions about the nature of algebra are answered. In addition, problems involving linear and quadratic equations are solved using the TI-Nspire graphing calculator. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series.

In this Investigation we get a historical overview of equations. This video is Segment 1 of a 2 segment series related to Variables and Equations.

In this Investigation we solve linear and quadratic equations. This video is Segment 3 of a 4 segment series related to Variables and Equations. Segments 3 and 4 are grouped together.

Video Tutorial: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles. In this tutorial, students review how to model equations with algebra tiles. Then the video focuses on how to solve multi-step equations with algebra tiles.

Description

This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction.

Description

This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction.

The following section reviews the basics of algebra tiles. Use this material as background material, and also as a supplement to the video series.

Description

This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction.

The following section reviews the basics of algebra tiles. Use this material as background material, and also as a supplement to the video series.

In this video segment, get an overview of variables and equations, along with the evolution of algebraic notation.

Topic

Equations

Definition

The "Not Equal To" symbol (≠) is used to indicate that two values are not equal.

Description

The "Not Equal To" symbol is crucial in mathematics as it denotes inequality between two expressions. This symbol is used in various mathematical contexts, such as solving inequalities, comparing numbers, and expressing conditions in algebraic equations. For example, in the inequality 𝑥 ≠ 5, it means that x can be any number except 5.

Topic

Equations

Definition

The Addition Property of Equality states that if you add the same value to both sides of an equation, the equality remains true.

Description

The Addition Property of Equality is a fundamental principle in algebra. It asserts that for any real numbers a, b, and c, if a = b, then a + c = b + c. This property is used to solve equations and maintain balance. For example, to solve x − 3 = 7, you add 3 to both sides to get x = 10.

Topic

Equations

Definition

An algebraic equation is a mathematical statement that shows the equality of two algebraic expressions. It's also another way of referring to a polynomial equation.

Description

Algebraic equations are central to algebra and involve variables, constants, and arithmetic operations. They are used to represent relationships and solve problems. For instance, the equation 2x + 3 = 7 can be solved to find x. Algebraic equations come in various forms, including linear, quadratic, and polynomial equations.

Topic

Equations

Definition

An algebraic expression is a combination of variables, constants, and arithmetic operations, without an equality sign.

Description

Algebraic expressions are fundamental components of algebra. They represent quantities and relationships without asserting equality. Examples include 3x + 4 and 5y − 2. Unlike equations, expressions cannot be solved but can be simplified or evaluated for given variable values.

Topic

Equations

Definition

Assigning values to variables involves giving specific values to variables in an equation or expression.

Description

Assigning values to variables is a fundamental process in algebra. It involves substituting variables with specific numbers to evaluate expressions or solve equations. For example, in the equation 

y = 2x + 3

assigning x = 4 gives y = 11.

Topic

Equations

Definition

A conditional equation is true only for specific values of the variable(s).

Description

Conditional equations are equations that hold true only under certain conditions or for specific variable values. For example, the equation 

x2 = 4 

is true only when x = 2 or x = −2. These equations contrast with identities, which are true for all variable values.

Topic

Equations

Definition

A constant term is a term in an algebraic expression that does not contain any variables.

Description

Constant terms are fixed values in algebraic expressions and equations. They do not change because they lack variables. For example, in the expression 

3x + 4

the number 4 is a constant term. Constant terms are essential in forming and solving equations.

Topic

Equations

Definition

The Division Property of Equality states that if you divide both sides of an equation by the same nonzero value, the equality remains true.

Description

The Division Property of Equality is a key principle in algebra. It states that for any real numbers a, b, and c (where 𝑐 ≠ 0), if 

a = b, then a ÷ c​ = b ÷ c 

This property is used to solve equations by isolating variables. For example, to solve 

3x = 12

divide both sides by 3 to get x = 4.

Topic

Equations

Definition

Equality is a mathematical statement that asserts that two expressions are equal.

Description

Equality is a foundational concept in mathematics. It indicates that two expressions have the same value, represented by the symbol "=". For example, in the equation 2 + 3 = 5, both sides are equal. Equality is used to form equations and solve problems.

In real-world applications, equality is used in accounting, engineering, and data analysis to ensure balance and accuracy. Understanding equality helps students develop logical reasoning and problem-solving skills.

Topic

Equations

Definition

An equation is a mathematical statement that asserts the equality of two expressions.

Description

Equations are central to mathematics, representing relationships between quantities. They consist of two expressions separated by an equals sign. For example, 

2x + 3 = 7

is an equation that can be solved to find x. Equations can be linear, quadratic, or polynomial, among others.

Topic

Equations

Definition

Equations in one variable involve a single variable and can be solved to find its value.

Description

Equations in one variable are fundamental in algebra. They typically take the form of ax + b = 0, where x is the variable. Solving these equations involves isolating the variable to determine its value. For example, solving 

2x + 3 = 7 

yields 

x = 2

Topic

Equations

Definition

Equations in two variables involve two variables and describe a relationship between them.

Description

Equations in two variables are essential in algebra and coordinate geometry. They typically take the form of 

ax + by = c

and represent lines in a coordinate plane. For example, the equation 

2x + 3y = 6

can be graphed as a line.

Topic

Equations

Definition

Equivalent equations are equations that have the same solutions.

Description

Equivalent equations are a key concept in algebra. They may look different but yield the same solutions. For instance, 

2x + 3 = 7

and 

4x + 6 = 14

are equivalent because both have the solution x = 2. Transformations such as addition, subtraction, multiplication, or division can produce equivalent equations.

Topic

Equations

Definition

A false equation is an equation that is not true for any value of the variable(s).

Description

False equations are equations that do not hold true for any value of the variable(s). For example, the equation 

x + 2 = x + 3

is false because there is no value of x that makes both sides equal. Identifying false equations is important in verifying the validity of mathematical statements.

Topic

Equations

Definition

An identity equation is true for all values of the variable(s).

Description

Identity equations are equations that hold true for all values of the variable(s). For example, the equation 

2(x + 1) = 2x + 2 

is an identity because it is true for any value of x. These equations are used to express mathematical identities and properties. In the equation above, the identity results from the use of the distributive property.

Topic

Equations

Definition

An inequation is a mathematical statement that shows the inequality between two expressions.

Description

Inequations, or inequalities, are statements that compare two expressions using inequality symbols such as >, <, ≥, and ≤. For example, 

x + 3 > 5 

indicates that 𝑥 x must be greater than 2. Inequations are used to represent constraints and conditions in mathematical models. Inequations sometimes involve the inequality symbol: ≠.

Topic

Equations

Definition

Isolating the variable involves manipulating an equation to get the variable alone on one side.

Description

Isolating the variable is a fundamental technique in algebra used to solve equations. It involves performing operations to both sides of an equation to get the variable by itself. For example, solving 

2x + 3 = 7

involves subtracting 3 and then dividing by 2 to isolate x, resulting in x = 2.

Topic

Equations

Definition

The left side of the equation refers to the expression on the left side of the equals sign.

Description

The left side of an equation is the part of the equation that appears before the equals sign. For example, in the equation 

2x + 3 = 7

the left side is 2x + 3. Understanding the left side of the equation is crucial for solving and balancing equations.

In real-world applications, recognizing the left side of an equation helps in setting up and solving problems accurately. It is essential for students to understand this concept to manipulate and solve equations effectively.

Topic

Equations

Definition

A linear equation is an equation that does not have an variables raised to a power higher than one. A linear equation can have one or more variables.

Description

Linear equations are fundamental in algebra and describe relationships are summarized below. 

Topic

Equations

Definition

A literal equation is an equation that involves two or more variables.

Description

Literal equations involve multiple variables and are used to express relationships between them. For example, the formula for the area of a rectangle, 

A = l•w

is a literal equation involving the variables l and w. Solving literal equations often involves isolating one variable in terms of the others.

Topic

Equations

Definition

A multi-step equation requires more than one step to solve.

Description

Multi-step equations involve multiple operations to isolate the variable. For example, solving 

3x + 2 = 11

requires subtracting 2 and then dividing by 3 to find x=3. These equations are common in algebra and require a systematic approach to solve.

In real-world applications, multi-step equations are used in complex problem-solving scenarios such as engineering and finance. Understanding how to solve multi-step equations helps students develop critical thinking and problem-solving skills.

Topic

Equations

Definition

The Multiplication Property of Equality states that if you multiply both sides of an equation by the same nonzero value, the equality remains true.

Description

The Multiplication Property of Equality is a fundamental principle in algebra. It states that for any real numbers a, b, and c (where 𝑐 ≠ 0), if 

a = b, then ac = bc

This property is used to solve equations by isolating variables. For example, to solve 

x/3 = 4

you multiply both sides by 3 to get x = 12.

Topic

Equations

Definition

A nonlinear equation is an equation that graphs as a curve and does not form a straight line.

Description

Nonlinear equations are equations that involve variables raised to powers other than one or involve products of variables. For example, the equation 

y = x2 

is nonlinear because it graphs as a parabola. These equations are used to model more complex relationships than linear equations.

Topic

Equations

Definition

A numerical expression is a mathematical phrase involving numbers and operation symbols, but no variables.

Description

Numerical expressions consist of numbers and operations such as addition, subtraction, multiplication, and division. For example, 

3 + 4 × 2

is a numerical expression. These expressions are evaluated to find their value.

In real-world applications, numerical expressions are used in everyday calculations such as budgeting, measuring, and data analysis. Understanding numerical expressions helps students perform arithmetic operations and develop computational skills.

Topic

Equations

Definition

A one-step equation requires only one operation to solve.

Description

One-step equations are the simplest type of equations in algebra. They involve a single operation to isolate the variable. For example, solving 

x + 3 = 7

requires subtracting 3 from both sides to find x = 4.

These equations are used in basic problem-solving scenarios and form the foundation for understanding more complex equations. Understanding one-step equations helps students develop confidence in solving algebraic problems and prepares them for advanced algebraic concepts.

Topic

Equations

Definition

A polynomial equation is an equation that involves a polynomial expression.

Description

Polynomial equations involve expressions that include terms with variables raised to whole-number exponents. For example, the equation 

x2 − 4x + 4 = 0 

is a polynomial equation. These equations can be linear, quadratic, cubic, etc., depending on the highest power of the variable.

Topic

Equations

Definition

A quadratic equation is a polynomial equation of degree 2, typically in the form ax2 + bx + c = 0.

Description

Quadratic equations are fundamental in algebra and involve variables raised to the second power. For example, the equation 

x2 − 4x + 4 = 0 

is quadratic. These equations can be solved using methods such as factoring, completing the square, and the quadratic formula.

Topic

Equations

Definition

The Reflexive Property of Equality states that any value is equal to itself.

Description

The Reflexive Property of Equality is a basic principle in mathematics. It states that for any value a, 

a = a

This property is used to justify steps in solving equations and proving mathematical statements.

In real-world applications, the reflexive property underlies the concept of identity and is fundamental in logical reasoning and proofs. Understanding this property helps students build a strong foundation in algebra and develop rigorous mathematical arguments.

Topic

Equations

Definition

The right side of the equation refers to the expression on the right side of the equals sign.

Description

The right side of an equation is the part of the equation that appears after the equals sign. For example, in the equation 

2x + 3 = 7

the right side is 7. Understanding the right side of the equation is crucial for solving and balancing equations.

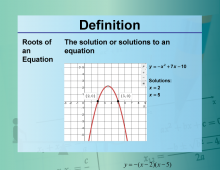
Topic

Equations

Definition

The roots of an equation are the values of the variable that satisfy the equation.

Description

The roots of an equation are the solutions that make the equation true. For example, the roots of the quadratic equation 

x2 − 4x + 4 = 0

are x = 2 because substituting 2 into the equation satisfies it. Finding roots is a fundamental task in algebra.

Topic

Equations

Definition

A solution is the value(s) of the variable(s) that satisfy an equation.

Description

The concept of solution is fundamental in equations, referring to the values that make the equation true. For example, in the equation 

x + 2 = 5

the solution is x = 3 because substituting 3 in place of x results in a true statement. Solutions can exist for various types of equations, whether single-variable, multi-variable, linear, or nonlinear.

Topic

Equations

Definition

Solving an equation involves finding the value(s) of the variable(s) that make the equation true.

Description

Solving an equation is a key skill in algebra, where one determines the values of variables that satisfy the equation. For example, in the equation 

2x + 3 = 7

one can find that x = 2 by isolating the variable through algebraic manipulations. Different techniques such as substitution, factoring, or using the quadratic formula may apply depending on the complexity of the equation.

Topic

Equations

Definition

The Subtraction Property of Equality states that if you subtract the same value from both sides of an equation, the equality remains true.

Description

The Subtraction Property of Equality is a fundamental principle in algebra. It states that for any real numbers a, b, and c, if 

a = b, then a − c = b − c

This property is used to solve equations by isolating variables. For example, to solve 

x + 3 = 7

you subtract 3 from both sides to get x = 4.