
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 6: Write Expressions Where Letters Stand for Numbers
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
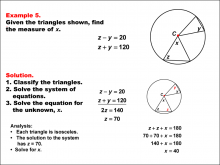
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 5 | Solving Equations Using Triangle Properties: Example 5TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles centered in a circle. The problem presents two equations: z - y = 20 and z + y = 120, where z and y represent angles in the isosceles triangles. The goal is to solve this system of equations to find the values of z and y, utilizing properties of isosceles triangles and circles. |
Applications of Equations and Inequalities and Applications of Triangles |
|
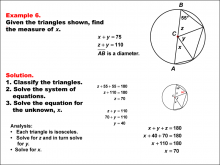
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 6 | Solving Equations Using Triangle Properties: Example 6TopicEquations DescriptionThis example explores solving equations involving triangles that share a vertex at the center of a circle. We are presented with two equations: x + y = 75 and z + y = 110, where x, y, and z represent angles in the triangle The goal is to solve this system of equations to find the values of x, y, and z, utilizing properties of isosceles triangles. Since each of the triangles is isosceles, we know that z + 55 + 55 = 180 and therefore, z = 70°. We substitute this into one of the equations: 70 + y = 110 7 = 40° |
Applications of Equations and Inequalities and Applications of Triangles |
|
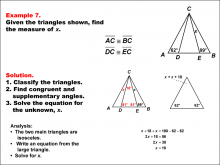
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 7 | Solving Equations Using Triangle Properties: Example 7TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles with a common vertex and base. We are given two angles, 62° and 99°, and need to find the unknown angle x. This problem demonstrates how to use the properties of isosceles triangles and the sum of angles in a triangle to solve for an unknown angle. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
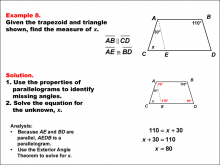
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 8 | Solving Equations Using Triangle Properties: Example 8TopicEquations DescriptionThis example involves solving an equation using the properties of a trapezoid with an embedded parallelogram and applying the exterior angle theorem. We are given two angles, 30° and 110°, and need to find the unknown angle x. This problem demonstrates the application of multiple geometric concepts to solve a complex equation. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
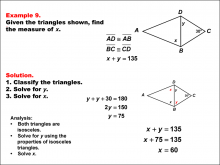
|
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 9 | Solving Equations Using Triangle Properties: Example 9TopicEquations DescriptionThis example focuses on solving equations using the properties of a kite and applying the exterior angle theorem. We are given one angle of 30° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 1 | Solving Equations with Angle Measures--Example 1TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 10 | Solving Equations with Angle Measures--Example 10TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 11 | Solving Equations with Angle Measures--Example 11TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 12 | Solving Equations with Angle Measures--Example 12TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 13 | Solving Equations with Angle Measures--Example 13TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 14 | Solving Equations with Angle Measures--Example 14TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 15 | Solving Equations with Angle Measures--Example 15TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
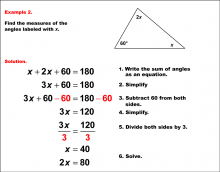
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 2 | Solving Equations with Angle Measures--Example 2TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 3 | Solving Equations with Angle Measures--Example 3TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 4 | Solving Equations with Angle Measures--Example 4TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 5 | Solving Equations with Angle Measures--Example 5TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
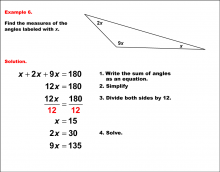
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 6 | Solving Equations with Angle Measures--Example 6TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 7 | Solving Equations with Angle Measures--Example 7TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 8 | Solving Equations with Angle Measures--Example 8TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 9 | Solving Equations with Angle Measures--Example 9TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
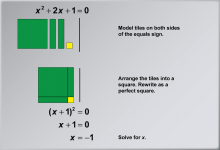
|
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 1 | Math Example: Solving Quadratic Equations with Algebra TilesTopicSolving Equations DescriptionIn this example, we explore solving the quadratic equation x2 + 2x + 1 = 0 using algebra tiles. The visual representation shows how to rearrange the equation into (x + 1)2 = 0, demonstrating the power of algebra tiles in simplifying complex equations. By arranging the tiles, students can physically see the relationship between the terms and understand how they combine to form a perfect square trinomial. |
Quadratic Equations and Functions |
|
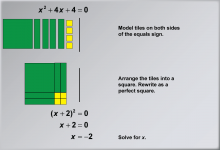
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 2 | Math Example: Solving Quadratic Equations with Algebra TilesTopicSolving Equations DescriptionThis example illustrates the process of solving the quadratic equation x2+ 4x + 4 = 0 using algebra tiles. The visual representation demonstrates how to rearrange the equation into (x + 2)2 = 0, showcasing the power of algebra tiles in simplifying and solving quadratic equations. By arranging the tiles, students can physically see how the terms combine to form a perfect square trinomial, making the solution process more intuitive. |
Quadratic Equations and Functions |
|
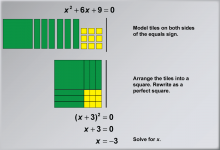
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 3 | Math Example: Solving Quadratic Equations with Algebra TilesTopicSolving Equations DescriptionThis example demonstrates the process of solving the quadratic equation x2 + 6x + 9 = 0 using algebra tiles. The visual representation shows how to rearrange the equation into (x + 3)2 = 0, illustrating the power of algebra tiles in simplifying and solving quadratic equations with larger coefficients. By arranging the tiles into a square, students can physically see how the terms combine to form a perfect square trinomial, making the solution process more intuitive and accessible. |
Quadratic Equations and Functions |
|
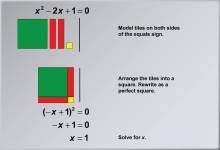
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 4 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 4TopicSolving Equations DescriptionIn this example, we explore solving the quadratic equation x2 - 2x + 1 = 0 using algebra tiles. The visual representation demonstrates how to arrange the tiles into a perfect square, effectively transforming the equation into (-x + 1)2 = 0. This method showcases the versatility of algebra tiles in handling equations with both positive and negative terms, as well as illustrating the completing the square technique. |
Quadratic Equations and Functions |
|
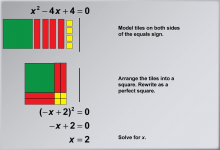
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 5 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 5TopicSolving Equations DescriptionThis example demonstrates the process of solving the quadratic equation x2 - 4x + 4 = 0 using algebra tiles. The visual representation shows how to arrange the tiles to form a perfect square, illustrating the completing the square method. By organizing the tiles, students can physically see how the terms combine to form the expression (-x + 2)2 = 0, making the solution process more intuitive and accessible. |
Quadratic Equations and Functions |
|
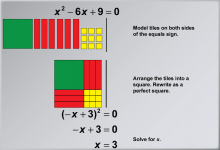
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 6 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 6TopicSolving Equations DescriptionThis example illustrates the process of solving the quadratic equation x2 - 6x + 9 = 0 using algebra tiles. By modeling tiles on both sides of the equation, students can visually understand the principle of maintaining equality while manipulating the equation. The tiles are arranged into a square to form a perfect square trinomial, demonstrating the completing the square method in a tangible way. |
Quadratic Equations and Functions |
|
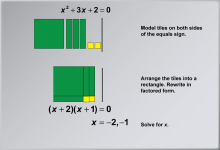
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 7 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 7TopicSolving Equations DescriptionThis example demonstrates the process of solving the quadratic equation x2 + 3x + 2 = 0 using algebra tiles. The visual representation shows how to arrange the tiles into a rectangle, illustrating the factoring method for solving quadratic equations. By organizing the tiles in this way, students can physically see how the terms combine to form the factored expression (x + 2)(x + 1) = 0, making the solution process more intuitive and accessible. |
Quadratic Equations and Functions |
|
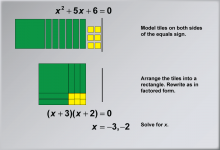
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 8 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 8TopicSolving Equations DescriptionThis example illustrates the process of solving the quadratic equation x2 + 5x + 6 = 0 using algebra tiles. The visual representation demonstrates how to arrange the tiles into a rectangle, showcasing the factoring method for solving quadratic equations. By organizing the tiles in this manner, students can physically see how the terms combine to form the factored expression (x + 3)(x + 2) = 0, making the solution process more concrete and understandable. |
Quadratic Equations and Functions |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition demonstrates solving the equation 2x + 3 = 7 by performing two inverse operations to isolate x. The operations shown are subtracting 3 from both sides and then dividing by 2. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 10 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 10TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition involves solving -3x + (-12) = -42 by performing two inverse operations: addition and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 2 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 2TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows solving the equation 3x + 4 = 13 by using two inverse operations. The steps involve subtracting 4 and then dividing by 3. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 3 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 3TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition involves solving the equation 2x + 4 = 8 using inverse operations. It shows subtraction and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 4 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 4TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition illustrates solving -4x + 5 = 25. It uses inverse operations by subtracting 5 and dividing by -4. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 5 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 5TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows the solution to -7x + 6 = 48 by isolating x with inverse operations, including subtraction and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 6 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 6TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition solves the equation 6x + (-2) = 34 by using inverse operations, specifically addition and division, to find the value of x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 7 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 7TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition solves 10x + (-6) = 54 by isolating x through inverse operations, including addition and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 8 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 8TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows solving -x + (-5) = 71 by performing inverse operations to isolate x, using addition and division by -1. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 9 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 9TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition demonstrates solving -2x + (-8) = 22 through inverse operations, specifically addition and division, to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction shows solving the equation 2x - 3 = 7 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 10 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 10TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation -3x - (-12) = -42 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 2 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 2TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction illustrates solving the equation 3x - 4 = 14 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 3 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 3TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation -2x - 4 = 8 by isolating x using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 4 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 4TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction explains solving the equation -x - 5 = 17 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 5 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 5TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction shows solving the equation -7x - 6 = 43 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 6 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 6TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction illustrates solving the equation 6x - (-2) = 38 by isolating x using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 7 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 7TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation 10x - (-6) = 76 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 8 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 8TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction explains solving the equation -x - (-5) = 71 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 9 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 9TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction shows solving the equation -2x - (-8) = 22 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: x/5 + 3 = 7. The solution is detailed with inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 10 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 10TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: -x/3 + (-12) = -42. The solution follows each step using inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |