
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 6: Write Expressions Where Letters Stand for Numbers
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Video Definition 19--Equation Concepts--Linear Equation | Video Definition 19--Equation Concepts--Linear Equation
TopicEquations DescriptionA Linear Equation is an equation where variables have an exponent of 1. Examples include x + 2 = 7, 2x + 3y = 4, and y = -2x + 10. Graphs of two-variable linear equations are straight lines. This term introduces a fundamental class of equations with specific properties, crucial for algebra and graphing. |
Applications of Linear Functions |

|
Video Definition 2--Equation Concepts--Addition Property of Equality | Video Definition 2--Equation Concepts--Addition Property of Equality
TopicEquations DescriptionThe Addition Property of Equality allows the addition of the same quantity to each side of an equation while maintaining equality. For example, if a = b, then a + c = b + c. This concept ensures equations can be manipulated while preserving their equality, demonstrated by solving x - 2 = 3 as x = 5 after adding 2 to both sides. This term introduces the basic manipulation of equations, forming the foundation for solving linear equations and maintaining equality. |
Applications of Equations and Inequalities |

|
Video Definition 20--Equation Concepts--Literal Equation | Video Definition 20--Equation Concepts--Literal Equation
TopicEquations DescriptionA Literal Equation includes more than one variable and often represents formulas, such as A = πr2, V = l*w*h, and SA = 2πr*h + 2πr2. This term connects to real-world applications and highlights the versatility of equations in representing formulas and relationships. |
Applications of Equations and Inequalities |

|
Video Definition 21--Equation Concepts--Multi-Step Equation | Video Definition 21--Equation Concepts--Multi-Step Equation
TopicEquations DescriptionA Multi-Step Equation involves more than two mathematical operations to solve. For example, 4x + 2 = 2x + 8 simplifies to x = 3 after subtraction and division steps. This term emphasizes solving more complex equations, showing sequential steps and reinforcing logical progression in algebra. |
Solving Multistep Equations |

|
Video Definition 22--Equation Concepts--Multiplication Property of Equality | Video Definition 22--Equation Concepts--Multiplication Property of Equality
TopicEquations DescriptionThe Multiplication Property of Equality allows multiplication by the same non-zero quantity on both sides of an equation, maintaining equality. For example, if a = b, then a * c = b * c. Solving x/2 = 3 yields x = 6 by multiplying both sides by 2. This term builds on equality principles and demonstrates another method for solving equations by manipulating terms. |
Applications of Equations and Inequalities |

|
Video Definition 23--Equation Concepts--Nonlinear Equation | Video Definition 23--Equation Concepts--Nonlinear Equation
TopicEquations DescriptionA Non-Linear Equation includes non-linear terms such as polynomials of degree 2 or higher, exponential, logarithmic, or trigonometric terms. Examples include y = x2 - 4x + 5 and y = sin(x). This term expands understanding beyond linear relationships, introducing diverse mathematical models and their applications. |
Applications of Equations and Inequalities |

|
Video Definition 24--Equation Concepts--Numerical Expression | Video Definition 24--Equation Concepts--Numerical Expression
TopicEquations DescriptionA Numerical Expression consists of numbers and operations without variables. Examples include 2 + 3 = 5 and 2(4 + 3) = 14. This term highlights fundamental operations, foundational for understanding and solving equations. The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Numerical Expressions |

|
Video Definition 25--Equation Concepts--One-Step Equation | Video Definition 25--Equation Concepts--One-Step Equation
TopicEquations DescriptionA One-Step Equation involves a single mathematical operation to solve. For example, x + 2 = 3 simplifies to x = 1 by subtraction. This term introduces the simplest form of equations, essential for beginners to build confidence and understanding in solving. |
Solving One-Step Equations |

|
Video Definition 26--Equation Concepts--Polynomial Equation | Video Definition 26--Equation Concepts--Polynomial Equation
TopicEquations DescriptionA Polynomial Equation consists of a polynomial expression equal to zero. Examples include x2 + 3x + 2 = 0 and x3 - 2x2 + 4x - 10 = 0. This term defines a key class of equations, critical for algebra and calculus studies. |
Polynomial Functions and Equations |

|
Video Definition 27--Equation Concepts--Quadratic Equation | Video Definition 27--Equation Concepts--Quadratic Equation
TopicEquations DescriptionA Quadratic Equation is a polynomial of degree 2. Examples include x2 - 2 = 23 and 2x2 + 3x + 2 = 0. Graphs of such equations are parabolas. This term extends understanding of polynomial equations, connecting algebra to geometry through parabolas. |
Quadratic Equations and Functions |

|
Video Definition 28--Equation Concepts--Reflexive Property of Equality | Video Definition 28--Equation Concepts--Reflexive Property of Equality
TopicEquations DescriptionThe Reflexive Property of Equality states that any quantity is equal to itself. Examples include 5 = 5 and x + 2 = x + 2. This term reinforces the foundational principle of equality, essential for logical reasoning in mathematics. |
Applications of Equations and Inequalities |

|
Video Definition 29--Equation Concepts--Right Side of the Equation | Video Definition 29--Equation Concepts--Right Side of the Equation
TopicEquations DescriptionRight Side of the Equation. The expression to the right side of the equals sign in an equation. 2x + 3 = x - 5 (right side highlighted) The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 3--Equation Concepts--Algebraic Equation | Video Definition 3--Equation Concepts--Algebraic Equation
TopicEquations DescriptionAn Algebraic Equation is another term for a polynomial equation, represented as a sum of terms equal to zero. Examples include x2 + 3x + 2 = 0 and x3 - 2x2 + 4x - 10 = 0. It highlights the structure of polynomial equations using constants, variables, and powers. This term connects to the topic by defining the types of equations learners encounter when solving or simplifying expressions. |
Applications of Equations and Inequalities |
|
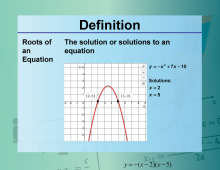
Video Definition 30--Equation Concepts--Roots of an Equation | Video Definition 30--Equation Concepts--Roots of an Equation
TopicEquations DescriptionRoots of an Equation. The solution or solutions to an equation. y = -x2 + 7x - 10; solutions: x = 2, x = 5 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 31--Equation Concepts--Solution | Video Definition 31--Equation Concepts--Solution
TopicEquations DescriptionSolution. A value for the unknown that turns a conditional equation into a true equation. For example, x = 5 is a solution to x + 2 = 7 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 32--Equation Concepts--Solving an Equation | Video Definition 32--Equation Concepts--Solving an Equation
TopicEquations DescriptionSolving an Equation. The process of finding the value(s) for a variable that result in a true equation. For example, x + 2 = 3 has a solution of x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 33--Equation Concepts--Subtraction Property of Equality | Video Definition 33--Equation Concepts--Subtraction Property of Equality
TopicEquations DescriptionSubtraction Property of Equality. The property that allows the subtraction of the same quantity from each side of an equation while maintaining the equality. For example, x + 2 = 3 becomes x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 34--Equation Concepts--Symmetric Property of Equality | Video Definition 34--Equation Concepts--Symmetric Property of Equality
TopicEquations DescriptionSymmetric Property of Equality. The property that states that an equation can be written two ways, with both sides interchanged. If a = b, then b = a. The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 35--Equation Concepts--The Unknown | Video Definition 35--Equation Concepts--The Unknown
TopicEquations DescriptionThe Unknown. In a conditional equation, the variable is also referred to as the unknown. 3x = 12, where x is the unknown The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Variables and Unknowns |

|
Video Definition 36--Equation Concepts--Transitive Property of Equality | Video Definition 36--Equation Concepts--Transitive Property of Equality
TopicEquations DescriptionTransitive Property of Equality. The property that states that two quantities equal to a third quantity are equal to each other. If a = b and b = c, then a = c The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 37--Equation Concepts--True Equation | Video Definition 37--Equation Concepts--True Equation
TopicEquations DescriptionTrue Equation. A mathematically accurate equation. If variables are involved, the true equation is for the values of the variable that make the equation true. Examples: 2 + 1 = 3; (2 + 3)2 = 25; x + 3 = 9 for x = 6 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 38--Equation Concepts--Two-Step Equation | Video Definition 38--Equation Concepts--Two-Step Equation
TopicEquations DescriptionTwo-Step Equation. A two-step equation is an equation that involves two mathematical operations to solve. The example given is 2x + 2 = 8, where the first operation is subtraction, leading to 2x = 6, followed by division to solve for x = 3. This concept extends the understanding of solving equations by introducing a sequence of operations, crucial for solving more complex equations. |
Solving Two-Step Equations |

|
Video Definition 39--Equation Concepts--Variable Expression | Video Definition 39--Equation Concepts--Variable Expression
TopicEquations DescriptionVariable Expression. A variable expression is made up of numbers, operations, and variables. Examples include 2x + 3 = 5 (expression on the left), 4 = 3x + 7 (expression on the right), and 4x + 3 = x - 5 (expressions on both sides). This connects variables to equations and highlights their role in forming relationships within mathematical contexts. |
Variable Expressions |

|
Video Definition 4--Equation Concepts--Algebraic Expression | Video Definition 4--Equation Concepts--Algebraic Expression
TopicEquations DescriptionAn Algebraic Expression consists of numbers, operations, and variables. Unlike equations, expressions may not have an equality. Examples include 2x + 3, 4 = 3x + 7, and 4x + 3 = x - 5, demonstrating their versatility in representing mathematical relationships. This term distinguishes between expressions and equations, forming the basis for manipulating algebraic forms before solving equations. |
Numerical and Algebraic Expressions |
|
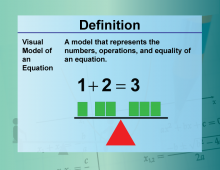
Video Definition 40--Equation Concepts--Visual Models for Equations | Video Definition 40--Equation Concepts--Visual Models for Equations
TopicEquations DescriptionVisual Model of an Equation. A visual model of an equation represents the numbers, operations, and equality using visuals. The example shows 1 + 2 = 3 with blocks illustrating the balance of the equation. This visual approach reinforces the foundational concept of equality and provides an intuitive way to understand equations, especially for visual learners. |
Applications of Equations and Inequalities |

|
Video Definition 41--Equation Concepts--Approximately Equal To | Video Definition 41--Equation Concepts--Approximately Equal To
TopicEquations DescriptionThe Approximately Equal To Sign (≈) indicates that two expressions are close in value but not equal. Examples include estimating sums (58 + 49 ≈ 100), square roots (√50 ≈ 7), and function values (f(x) ≈ 25). This term relates to the topic by introducing estimation techniques, valuable for checking solutions or simplifying problems. |
Applications of Equations and Inequalities |

|
Video Definition 42--Equation Concepts--Proportional To | Video Definition 42--Equation Concepts--Proportional To
TopicEquations DescriptionProportional To indicates a linear relationship between two variables. For example, distance (d) is proportional to time (t), written as d ∝ t. This term links linear equations to real-world relationships, reinforcing practical applications of mathematical concepts. |
Applications of Equations and Inequalities |
|
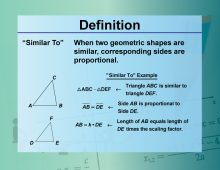
Video Definition 43--Equation Concepts--Similar To | Video Definition 43--Equation Concepts--Similar To
TopicEquations DescriptionSimilar To. When two geometric shapes are similar, corresponding sides are proportional. ΔABC ~ ΔDEF; AB ∝ DE The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 44--Equation Concepts--Congruent To | Video Definition 44--Equation Concepts--Congruent To
TopicEquations DescriptionCongruent To signifies that two geometric shapes are congruent, meaning their corresponding sides and angles are equal. For example, triangles ABC and DEF are congruent, so side AB equals side DE. This term introduces geometric equality, tying equations to geometric properties and congruence criteria. |
Applications of Equations and Inequalities |

|
Video Definition 5--Equation Concepts--Assigning Values to Variables | Video Definition 5--Equation Concepts--Assigning Values to Variables
TopicEquations DescriptionAssigning Values to Variables involves assigning a numerical value to a variable for evaluating functions. For instance, let x = 3 in f(x) = 2x + 8 yields f(3) = 14. This term supports understanding how to evaluate equations and functions by substituting values, a key step in problem-solving. |
Variable Expressions |

|
Video Definition 6--Equation Concepts--Conditional Equation | Video Definition 6--Equation Concepts--Conditional Equation
TopicEquations DescriptionA Conditional Equation is true only for specific variable values. Examples include x + 1 = 4 (x = 3), x2 - 25 = 0 (x = ±5), and 2x - 5 = x + 9 (x = 14). This term supports solving equations by emphasizing that solutions depend on satisfying the given conditions. |
Applications of Equations and Inequalities |

|
Video Definition 7--Equation Concepts--Constant Term | Video Definition 7--Equation Concepts--Constant Term
TopicEquations DescriptionA Constant Term in an algebraic equation is a number without a variable. Examples include 2 in x2 + 3x + 2 = 0, -10 in x3 - 2x2 + 4x - 10 = 0, and 5 in x4 - 2x3 + 4x2 - x + 5 = 0. This term explains the role of constants in equations, crucial for identifying and isolating terms when solving equations. |
Variables and Unknowns |

|
Video Definition 8--Equation Concepts--Division Property of Equality | Video Definition 8--Equation Concepts--Division Property of Equality
TopicEquations DescriptionThe Division Property of Equality allows division by the same non-zero quantity on both sides of an equation, maintaining equality. For example, if a = b, then a / c = b / c, where c ≠ 0. Solving 5x = 15 yields x = 3 by dividing both sides by 5. This term builds on equality principles, showing another method to isolate variables and solve equations. |
Applications of Equations and Inequalities |

|
Video Definition 9--Equation Concepts--Equality | Video Definition 9--Equation Concepts--Equality
TopicEquations DescriptionEquality refers to a mathematical statement where two expressions are equal. Examples include 1 + 2 = 3 and x + 3 = 7, where both sides represent the same value. This term defines the core concept of equations, ensuring all manipulations preserve equality to find solutions. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Applications: Inequalities | Video Transcript: Algebra Applications: Inequalities
This is the transcript for the video of same title. Video contents: In this episode of Algebra Applications, two real-world explorations of inequalities are developed: Hybrid Cars. An examination of the equations and inequalities that involve miles per gallon (mpg) for city and highway traffic reveals important information about hybrid cars and those with gasoline-powered engines. Floods in Venice. Venice experiences a great deal of flooding, and with the expected rise of sea levels over the next century, this ancient city is in peril. Through a series of inequalities, students analyze the impact of flooding. |
Inequalities |

|
Video Transcript: Algebra Applications: Inequalities, Segment 1: Hybrid Cars. | Video Transcript: Algebra Applications: Inequalities, Segment 1: Hybrid Cars.
This is the transcript for the video of same title. Video contents: With the increasing demand worldwide for cars, the cost of gasoline continues to rise. The need for fuel-efficient cars makes hybrids a current favorite. An examination of the equations and inequalities that involve miles per gallon (mpg) for city and highway traffic reveals important information about hybrid cars and those with gasoline-powered engines. Students use the Graphs and Geometry features of the TI-Nspire. |
Inequalities |

|
Video Transcript: Algebra Applications: Inequalities, Segment 2: Floods in Venice | Video Transcript: Algebra Applications: Inequalities, Segment 2: Floods in Venice
This is the transcript for the video of same title. Video contents: The city of Venice is slowly sinking into the Adriatic Sea. So what does a city whose streets are full of water do about flooding? Venice experiences a great deal of flooding, and with the expected rise of sea levels over the next century, this ancient city is in peril. Through a series of inequalities, students analyze the impact of flooding, rising sea levels, and sinking have on this grand, ancient city. Students use the Lists and Spreadsheets and the Program Editor features of the TI-Nspire. |
Inequalities |

|
Video Transcript: Algebra Applications: Variables and Equations | Video Transcript: Algebra Applications: Variables and Equations
This is the transcript for the video of same title. Video contents: In this episode of Algebra Applications, two real-world explorations are developed: Biology. Analyzing statistics from honey bee production allows for a mathematical analysis of the so-called Colony Collapse Disorder. Geology. Why do rivers meander instead of traveling in a straight line? In this segment the geological forces that account for a river??s motion are explained. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Solving One-Step Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Solving One-Step Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Solving Two-Step Equations | Video Transcript: Algebra Tiles: Solving Two-Step Equations
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Tutorial: Algebra Tiles 17 | Video Tutorial: Algebra Tiles 17
TopicExpressions and Equations DescriptionThis video explains solving one-step equations like x + 2 = 4 and x ÷ 2 = 4 with algebra tiles. It covers addition, subtraction, multiplication, and division operations. Key vocabulary includes one-step equations, zero pairs, and operations. |
Algebra Tiles--Expressions and Equations |

|
Video Tutorial: Algebra Tiles 18 | Video Tutorial: Algebra Tiles 18
TopicExpressions and Equations DescriptionThe video discusses solving two-step equations like 2x + 2 = 4 using algebra tiles. It shows a multi-stage process for isolating variables, including handling subtraction as addition. Key vocabulary includes two-step equations, multi-stage process, and integer tiles. |
Algebra Tiles--Expressions and Equations |

|
Video Tutorial: Algebra Tiles 19 | Video Tutorial: Algebra Tiles 19
TopicExpressions and Equations DescriptionThis video covers multi-step equations, such as 3x + 2 = x + 4, using algebra tiles. It demonstrates how to isolate variables through a multi-stage process involving addition and subtraction. Key vocabulary includes multi-step equations, isolation, and operations. |
Algebra Tiles--Expressions and Equations |

|
VIDEO: Algebra Applications: Variables and Equations, 1 | VIDEO: Algebra Applications: Variables and Equations, 1
TopicEquations DescriptionThe video introduces algebraic expressions and their ability to represent both known and unknown quantities. It defines variables as placeholders for unknowns and explains equations as relationships between two expressions. Key concepts include solving for variables and understanding the role of variables in equations. Key vocabulary includes variable, unknown quantity, and equation. The applications discussed include investigations into real-world scenarios such as honeybee populations and river geology. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
VIDEO: Algebra Applications: Variables and Equations, 2 | VIDEO: Algebra Applications: Variables and Equations, 2
TopicEquations DescriptionThis segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
VIDEO: Algebra Applications: Variables and Equations, 3 | VIDEO: Algebra Applications: Variables and Equations, 3
TopicEquations DescriptionThe video investigates the geometry of river meanders using the concept of the meander ratio, calculated as the ratio of a river’s sinuous length to its straight-line length. It uses a TI-Nspire calculator to simulate river paths and compute ratios. Key vocabulary includes meander ratio, sinuous length, and geometric modeling. Applications highlight the mathematical modeling of natural phenomena and the occurrence of pi in nature. |
Applications of Equations and Inequalities, Variables and Unknowns, Variable Expressions and Applications of Ratios, Proportions, and Percents |

|
VIDEO: Algebra Nspirations: Variables and Equations, 1 | VIDEO: Algebra Nspirations: Variables and Equations, 1
TopicEquations DescriptionThis video covers the historical evolution of equations, the role of variables, constants, and parameters, and introduces linear and quadratic equations. Key vocabulary includes symbolic algebra, parameter, variable, and constants. Real-world applications are introduced through general problem-solving using linear equations, like solving for unknowns in financial contexts. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
VIDEO: Algebra Nspirations: Variables and Equations, 2 | VIDEO: Algebra Nspirations: Variables and Equations, 2
TopicEquations DescriptionIn this Math Lab explore the linear relationship between the circumference and diameter of a circle. Relevance to the Topic: This video is a valuable resource for understanding the topic of Equations. It connects theoretical concepts with practical applications, offering insights that make learning engaging and relatable. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
VIDEO: Algebra Nspirations: Variables and Equations, 3 | VIDEO: Algebra Nspirations: Variables and Equations, 3
TopicEquations DescriptionExpanding on Part 1, this video demonstrates solving linear equations algebraically and dynamically using TI-Nspire technology. Applications include walk-a-thons and bike-a-thons, illustrating linear relationships in practical contexts. Key vocabulary includes linear equation, function, and symbolic representation. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |