Illustrative Math Alignment: Grade 6 Unit 1

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion where b is expressed as x + 1, and c and d are given constants (c = 3, d = 2). The goal is to solve for a using the proportion a / b = c / d. By substituting the known values, we set up the equation a / (x + 1) = 3 / 2 and solve for a, resulting in the expression a = (3(x + 1)) / 2.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles right triangles with algebraic expressions. Two 45-45-90 triangles are shown, with one having sides labeled 15√2 and 15, and the other having sides labeled √2 * 5x and y. The problem requires finding the length of y in terms of x using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles triangles. Two isosceles triangles are shown, with the smaller one having sides of 30 and 16, and the larger one having sides of x and 20. The problem requires finding the length of side x by setting up a proportion: 30 / 16 = x / 20. Solving this equation leads to x = 37.5.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles triangles with algebraic expressions. Two isosceles triangles are shown, with the smaller one having sides of 22 and 12, and the larger one having sides of 10x + 5 and 6x. The problem requires setting up a proportion: 22 / 12 = (10x + 5) / 6x. Solving this equation leads to x = 5, which then allows us to find the side lengths of the larger triangle.

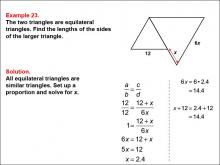
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar equilateral triangles. Two equilateral triangles are shown, with the smaller one having a side length of 12, and the larger one having a side length of 6x and an additional side labeled as 12 + x. The problem requires finding the lengths of the sides of the larger triangle by setting up a proportion: 12 / 12 = (12 + x) / 6x. Solving this equation leads to x = 2.4, and the length of the larger triangle's side is found to be approximately 14.4 units.

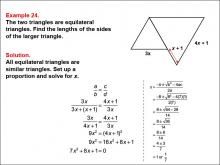
Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a complex proportion problem using similar equilateral triangles with algebraic expressions. Two equilateral triangles are shown, with the smaller one having a side length of 3x, and the larger one having side lengths labeled as (4x + 1) and (x + 1). The problem requires setting up a proportion: 3x / (4x + 1) = 3x / (3x + (x + 1)). Solving this equation leads to a quadratic equation, which when solved gives x ≈ 7/1.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar rectangles. Two rectangles are shown, with the smaller one having sides of 2 and 3, and the larger one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 2 / 3 = x / 15. Solving this equation leads to x = 10.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar rectangles with algebraic expressions. Two rectangles are shown, with the smaller one having sides of 5 and 12, and the larger one having sides of x + 5 and 3x + 6. The problem requires setting up a proportion: 5 / 12 = (x + 5) / (3x + 6). Solving this equation leads to x = 10, which then allows us to find the side lengths of the larger rectangle as 15 and 36.

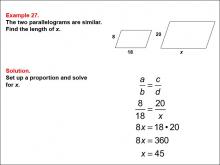
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar parallelograms. Two parallelograms are shown, with the smaller one having sides of 8 and 18, and the larger one having sides of 20 and x. The problem requires finding the length of side x by setting up a proportion: 8 / 18 = 20 / x. Solving this equation leads to x = 45.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, with the smaller one having sides of 9 and 21, and the larger one having sides of x + 12 and 4x + 3. The problem requires setting up a proportion: 9 / 21 = (x + 12) / (4x + 3). Solving this equation leads to x = 15, which then allows us to find the side lengths of the larger parallelogram as 27 and 63.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two triangles are similar using proportions. Two triangles are shown, both with a 70° angle. The first triangle has sides of 12 and 10, while the second has sides of 18 and 15. The problem requires setting up a proportion to check for similarity: 12 / 10 = 18 / 15. After simplifying, both ratios are equal (6 / 5 = 6 / 5), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for b in a proportion where a = 8, c = 4, and d = 3. We set up the proportion 8 / b = 4 / 3 and solve for b, resulting in b = 6. This problem shows how to find an unknown value in the denominator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two triangles are not similar using proportions. Two triangles are shown, both with a 75° angle. The first triangle has sides of 15 and 9, while the second has sides of 28 and 18. The problem requires setting up a proportion to check for similarity: 15 / 9 = 28 / 18. After simplifying, the ratios are not equal (5 / 3 ≠ 14 / 9), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two right triangles are similar using proportions. Two right triangles are shown, one with legs of length 4 and 3, and the other with legs of length 10 and 7.5. The problem requires setting up a proportion to check for similarity: 4 / 3 = 10 / 7.5. After simplifying, both ratios are equal (4 / 3 = 4 / 3), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two right triangles are not similar using proportions. Two right triangles are shown, one with legs of length 12 and 5, and the other with legs of length 35 and 15. The problem requires setting up a proportion to check for similarity: 12 / 5 = 35 / 15. After simplifying, the ratios are not equal (12 / 5 ≠ 7 / 3), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two rectangles are similar using proportions. Two rectangles are shown, with the first having dimensions 3 and 8, and the second having dimensions 9 and 24. The problem requires setting up a proportion to check for similarity: 3 / 8 = 9 / 24. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two rectangles are similar using proportions with algebraic expressions. Two rectangles are shown, with the first having dimensions 11.5 and 23, and the second having dimensions 23x and 46x. The problem requires setting up a proportion to check for similarity: 11.5 / 23 = 23x / 46x. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar for any value of x.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two parallelograms are similar using proportions. Two parallelograms are shown, with the first having dimensions 6 and 9, and the second having dimensions 15 and 22.5. The problem requires setting up a proportion to check for similarity: 6 / 9 = 15 / 22.5. After simplifying, the ratios are equal, confirming that the parallelograms are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two parallelograms are not similar using proportions. Two parallelograms are shown, with the first having dimensions 9 and 28, and the second having dimensions 18 and 54. The problem requires setting up a proportion to check for similarity: 9 / 18 ≠ 28 / 54. After simplifying, the ratios are not equal, concluding that the parallelograms are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with side lengths 9 and 18, and the other with expressions 6x and 10x + 6. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 9 / 18 = 6x / (10x + 6). Solving this equation leads to x = 3.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with side lengths 4 and 3, and the other with expressions 3x and 2x + 1. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 4 / 3 = 3x / (2x + 1). Solving this equation leads to x = 4.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar rectangles with an unknown side length. Two rectangles are shown, one with side lengths of 4 and x, and the other with side lengths of 15 and 4. The problem requires setting up a proportion to determine the value of x for which the rectangles are similar: 4 / 15 = x / 4. Solving this equation leads to x = 16/15.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for b in a proportion where a is expressed as x + 2, and c and d are given constants (c = 5, d = 2). We set up the equation (x + 2) / b = 5 / 2 and solve for b, resulting in the expression b = (2(x + 2)) / 5. This problem demonstrates how to handle algebraic expressions in proportions.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, one with side lengths of 6 and x, and the other with expressions of 3x + 2 and 22. The problem requires setting up a proportion to determine the value of x for which the parallelograms are similar: 6 / 22 = x / (3x + 2). Solving this equation leads to x = 3.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for c in a proportion where a = 9, b = 4, and d = 12. We set up the proportion 9 / 4 = c / 12 and solve for c, resulting in c = 27. This problem shows how to find an unknown value in the numerator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for c in a proportion where a = 8, b = 3, and d is expressed as x + 3. We set up the equation 8 / 3 = c / (x + 3) and solve for c, resulting in the expression c = (8(x + 3)) / 3. This problem demonstrates how to handle algebraic expressions in the denominator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for d in a proportion where a = 12, b = 5, and c = 48. We set up the proportion 12 / 5 = 48 / d and solve for d, resulting in d = 20. This problem shows how to find an unknown value in the denominator of a proportion when all other values are known.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for d in a proportion where a = 11, b = 5, and c is expressed as x - 4. We set up the equation 11 / 5 = (x - 4) / d and solve for d, resulting in the expression d = (5(x - 4)) / 11. This problem demonstrates how to handle algebraic expressions in the numerator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar triangles. Two triangles are shown, with one having sides of 3 and 4, and the other having sides of 6 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 3 / 4 = 6 / x. Solving this equation leads to x = 8.

Topic

Equations

Description

This example demonstrates solving equations using angle properties, specifically focusing on supplementary angles. Supplementary angles are two angles that add up to 180 degrees. In this case, we have one known angle of 135° and an unknown angle x. 

To solve such equations, we use the fundamental property of supplementary angles: their sum equals 180°. 

Topic

Equations

Description

This example illustrates solving equations using angle properties, focusing on parallel lines cut by a transversal and supplementary angles. When parallel lines are cut by a transversal, pairs of supplementary angles are formed, meaning they sum to 180°. 

In this scenario, we have one known angle of 118° and an unknown angle x. However, angle y and the 118° angle are alternate exterior angles, which are congruent. This means we can set up this equation using the property of supplementary angles:

118 + x = 180

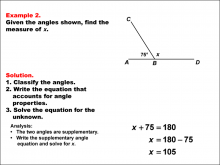
Topic

Equations

Description

This example illustrates solving equations using angle properties, focusing on supplementary angles. Supplementary angles are two angles that sum to 180 degrees. In this scenario, we have one known angle of 75° and an unknown angle x. The equation for supplementary angles is always in the form: angle1 + angle2 = 180°. 

Here, we can write 75 + x = 180. To solve for x, we subtract 75 from both sides: x = 180 - 75, giving us x = 105°. 

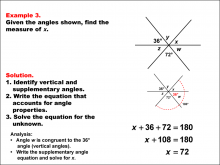
Topic

Equations

Description

This example demonstrates solving equations using angle properties, specifically focusing on straight angles and vertical angles. A straight angle measures 180°, and vertical angles are always congruent. In this scenario, we have two known angles (36° and 72°) and an unknown angle x. This unknown angle x is vertical (and therefore congruent) to angle z. 

The angles 36, 72, and z form a straight, but since z is congruent to x, we can write the sum of this straight angle:

x + 36 + 72 = 180

x = 72°

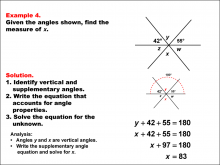
Topic

Equations

Description

This example illustrates solving equations using angle properties, focusing on straight angles and vertical angles. A straight angle measures 180°, and vertical angles are always congruent. In this scenario, we have two known angles (42° and 55°) and an unknown angle x. However, angle x is vertical (and therefore congruent) to angle y.

The equation can be set up based on the fact that the sum of angles on a straight line is 180°. Thus, we have: 

42 + 55 + x = 180

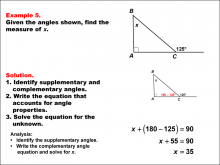
Topic

Equations

Description

This example demonstrates solving equations using angle properties, specifically focusing on complementary angles and the exterior angle theorem. Complementary angles are two angles that sum to 90°, while the exterior angle theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. In this scenario, we have a right angle (90°), an exterior angle (125°), and an unknown angle x. Using the exterior angle theorem, we can set up the equation: x + 90 = 125. To solve for x, we subtract 90 from both sides: x = 35°. 

Topic

Equations

Description

This example illustrates solving equations using angle properties, focusing on an isosceles right triangle. An isosceles right triangle has a right angle (90°) and two equal angles. In this scenario, we have the right angle given, and the two unknown equal angles represented by x. 

The equation can be set up based on the fact that the sum of angles in a triangle is 180°. Thus, we have: 

90 + x + x = 180, or simplified, 90 + 2x = 180

To solve for x, we first subtract 90 from both sides: 2x = 90. Then, dividing both sides by 2, we get: x = 45°. 

Topic

Equations

Description

This example demonstrates solving equations using angle properties, specifically focusing on parallel lines cut by a transversal and same side interior angles. When parallel lines are cut by a transversal, same side interior angles are supplementary, meaning they sum to 180°. 

In this scenario, we have one known angle of 112° and an unknown angle x. The 112° angle is vertical to the same side interior angle paired with x. The equation can be set up as: 

112 + x = 180

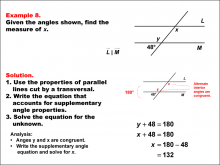
Topic

Equations

Description

This example illustrates solving equations using angle properties, focusing on parallel lines cut by a transversal and alternate interior angles. When parallel lines are cut by a transversal, alternate interior angles are congruent, meaning they have the same measure. In this scenario, we have one known angle of 48° and an unknown angle x. Since x and y are alternate interior angles, they are congruent. 

We can now use the property of supplementary angles to solve for x:

x + 48 = 180

x = 132°

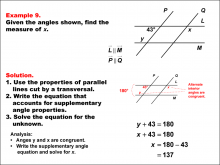
Topic

Equations

Description

This example demonstrates solving equations using angle properties, specifically focusing on parallel lines cut by a transversal and alternate interior angles. When parallel lines are cut by a transversal, alternate interior angles are congruent, meaning they have the same measure. 

In this scenario, we have one known angle of 43° and an unknown angle x. However, angle x and angle y are alternate interior angles and are congruent. This means that x and teh 43° angle are same side interior angles, which are supplementary. We set up this equation:

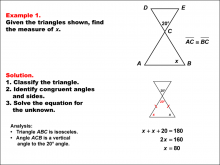
Topic

Equations

Description

This example focuses on solving equations using the properties of similar isosceles triangles. Isosceles triangles are characterized by having two equal sides and two equal base angles. In this case, we have two similar isosceles triangles, which means they share the same shape but may differ in size. The equation to be solved involves finding the unknown angle x, given that one of the angles is 20°. The property of vertical angles tells us that the angle vertical to the 20° angle is also 20°

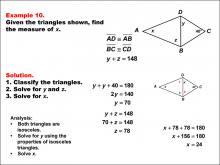
Topic

Equations

Description

This example, similar to Example 9, involves solving equations using the properties of a kite and applying the exterior angle theorem. We are again given one angle of 40° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. 

Key properties to consider: 

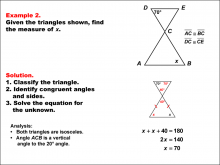
Topic

Equations

Description

This example explores solving equations using the properties of similar isosceles triangles, building upon the concepts introduced in Example 1. In this case, we have two similar isosceles triangles with one known angle of 70° and an unknown angle x. The goal is to determine the value of x using triangle properties and algebraic techniques. 

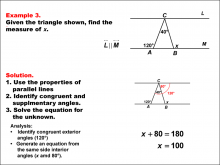
Topic

Equations

Description

This example focuses on solving equations involving parallel lines cut by a transversal, a fundamental concept in geometry. The problem presents two parallel lines intersected by two transversals that also form a triangle. We are given that one angle measures 120° and the corresponding angle can be expressed as (y + 40)°. The goal is to determine the value of y using the properties of angles formed by parallel lines and a transversal. 

When parallel lines are cut by a transversal, several important angle relationships are formed: 

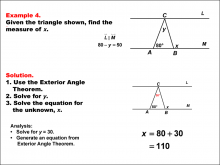
Topic

Equations

Description

This example demonstrates solving equations using the Exterior Angle Theorem in the context of parallel lines cut by a transversal, two crucial concepts in geometry. The problem presents a triangle with two known interior angles of 80° and y, and an unknown exterior angle x°. 

We are also given that 80 - y = 50, which simplifies to y = 30. The goal is to determine the value of x using the properties of triangles and the Exterior Angle Theorem. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Wo we get x = 80 + 30, or x = 110.