Illustrative Math Alignment: Grade 6 Unit 8

Solve a word search puzzle on the topic of Data Analysis.

Related Resources

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity.

Related Resources

Worksheet Library

This is the transcript for the video of same title. Video contents: In this Math Lab a hands-on probability activity involving coins is explored.

To see the complete collection of video transcriptsy, click on this link.

This is the transcript for the video of same title. Video contents: In this Investigation we explore uncertainty and randomness.

To see the complete collection of video transcriptsy, click on this link.

This is the transcript for the video of same title. Video contents: What are the two meanings of statistics? What does it really mean that an event has a 50% probability of occurring? Why are data analysis and probability always taught together? Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video answers these questions and addresses fundamental concepts such as the law of large numbers and the notion of regression analysis. Both engaging investigations are based on true stories and real data, utilize different TI-Nspire iPad Applications, and model the seamless connection among various problem representations. Concepts explored: statistics, data analysis, regression analysis

This is the transcript for the video of same title. Video contents: Honey bees not only produce a tasty treat, they also help pollinate flowering plants that provide much of the food throughout the world. So, when in 2006 bee colonies started dying out, scientists recognized a serious problem. Analyzing statistics from honey bee production allows for a mathematical analysis of the so-called Colony Collapse Disorder.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 28, 49, 1, -19, -37, 43, 27, 32, -10, 39, -19, -48, -49, 28, 36, 37, 44, 42, 29, -17. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 98. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 42, 31, 16, 0, 35, 26, 30, 14, 6, 2, 13, 37, 33, 36, 19, 48, 3, 9, 45, 12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of non-negative numbers and find their difference.

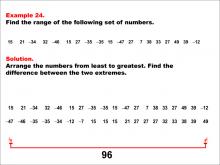
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

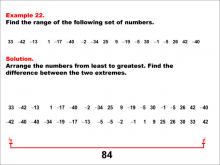
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range.

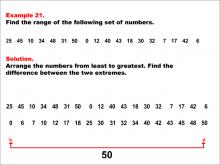
Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

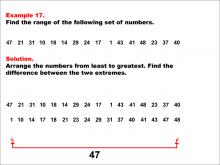
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

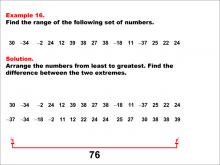
Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 16, 50, 24, 31, 30, 6, 22, 32, 43, 27, 48, 17, 36. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 44. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: -33, 38, 29, -8, 12, 2, 36, -8, 12, 18, -23, 50. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 83. This example is particularly useful as it includes both positive and negative numbers, helping students understand how to handle different types of values when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of a set of numbers: 22, 13, 15, 1, 16, 28, 3, 5, 18, 42, 8, 9. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 41. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a set of numbers and find their difference. The process encourages critical thinking and helps students visualize the relationship between numbers in a dataset.

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Description

This example illustrates the process of finding the median for the set of numbers: 0, 25, 26, 49, 39, 27, 1, 27, 38, 49, 10, 40. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of 27.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the median of the following set of numbers: 50, 14, 47, 43, 25, 10, 18, 21, 20, 19. The process involves arranging the numbers in ascending order and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of 20.5.

Topic

Measures of Central Tendency

Description

This example illustrates the process of finding the median for the set of numbers: 13, -3, 23, -20, -14, -32, -31, -21, 36, -14. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of -14.

Topic

Measures of Central Tendency

Description

This example demonstrates finding the median of the following set of numbers: 6, -19, 38, 47, 46, -46, 15, 10, 24, 16. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of 15.5.

Topic

Measures of Central Tendency

Description

This example illustrates the process of finding the median for the set of numbers: 50, 41, 30, 30, 47, 31, 45, 12, 6, 14, 39. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 31.

Topic

Measures of Central Tendency

Description

This example demonstrates finding the median of the following set of numbers: -24, 50, -22, -27, 43, 41, 1, 27, -13, 7, 0. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 1.

Topic

Measures of Central Tendency

Description

This example illustrates the process of finding the median for the set of numbers: 2, -20, -5, 45, -15, 6, 27, 21, -17, -1, -31, -1. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of -1.