Illustrative Math Alignment: Grade 7 Unit 4
Proportional Relationships and Percentages
Lesson 9: More and Less than 1%
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
Math Example--Percents--Equations with Percents: Example 31 | Math Example--Percents--Equations with Percents: Example 31TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "4 is 0.1% of what number?" The solution involves setting up the equation 4 = 0.001 * x, then solving for x to get x = 4 / 0.001, which equals 4000. This example demonstrates how to calculate the whole when given a very small percentage of it, resulting in a much larger number. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 32 | Math Example--Percents--Equations with Percents: Example 32TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "7 is 1% of what number?" The solution involves setting up the equation 7 = 0.01 * x, then solving for x to get x = 7 / 0.01, which equals 700. This example introduces a scenario where we need to find the whole when given a small percentage of it, resulting in a number 100 times larger than the given value. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 33 | Math Example--Percents--Equations with Percents: Example 33TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is 30% of what number?" The solution involves setting up the equation 9 = 0.3 * x, then solving for x to get x = 9 / 0.3, which equals 30. This example demonstrates how to calculate the whole when given a larger percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 34 | Math Example--Percents--Equations with Percents: Example 34TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "1 is 400% of what number?" The solution involves setting up the equation 1 = 4.0 * x, then solving for x to get x = 1 / 4, which equals 0.25. This example introduces a scenario where we need to find a number that, when increased by 400%, results in 1, leading to a fraction or decimal less than 1. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 35 | Math Example--Percents--Equations with Percents: Example 35TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "15 is 0.25% of what number?" The solution involves setting up the equation 15 = 0.0025 * x, then solving for x to get x = 15 / 0.0025, which equals 6000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 36 | Math Example--Percents--Equations with Percents: Example 36TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "30 is 5% of what number?" The solution involves setting up the equation 30 = 0.05 * x, then solving for x to get x = 30 / 0.05, which equals 600. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a much larger number. |
Solving Percent Equations |
|
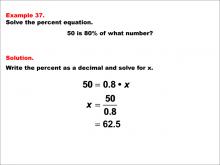
Math Example--Percents--Equations with Percents: Example 37 | Math Example--Percents--Equations with Percents: Example 37TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "50 is 80% of what number?" The solution involves setting up the equation 50 = 0.8 * x, then solving for x to get x = 50 / 0.8, which equals 62.5. This example introduces a scenario where we need to find the whole when given a large percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |
|
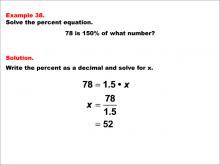
Math Example--Percents--Equations with Percents: Example 38 | Math Example--Percents--Equations with Percents: Example 38TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "78 is 150% of what number?" The solution involves setting up the equation 78 = 1.5 * x, then solving for x to get x = 78 / 1.5, which equals 52. This example demonstrates how to calculate the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |
|
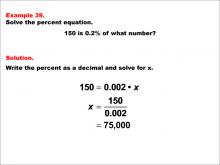
Math Example--Percents--Equations with Percents: Example 39 | Math Example--Percents--Equations with Percents: Example 39TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "150 is 0.2% of what number?" The solution involves setting up the equation 150 = 0.002 * x, then solving for x to get x = 150 / 0.002, which equals 75,000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 4 | Math Example--Percents--Equations with Percents: Example 4TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 6.5% of 45.5?" The solution involves converting 6.5% to its decimal equivalent, 0.065, and then multiplying it by 45.5 to obtain the result of 2.9575. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation. |
Solving Percent Equations |
|
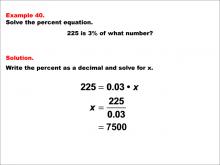
Math Example--Percents--Equations with Percents: Example 40 | Math Example--Percents--Equations with Percents: Example 40TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "225 is 3% of what number?" The solution involves setting up the equation 225 = 0.03 * x, then solving for x to get x = 225 / 0.03, which equals 7,500. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 41 | Math Example--Percents--Equations with Percents: Example 41TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is 40% of what number?" The solution involves setting up the equation 400 = 0.4 * x, then solving for x to get x = 400 / 0.4, which equals 1000. This example demonstrates how to calculate the whole when given a significant percentage of it, resulting in a number that is larger than the given value. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 42 | Math Example--Percents--Equations with Percents: Example 42TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "650 is 130% of what number?" The solution involves setting up the equation 650 = 1.3 * x, then solving for x to get x = 650 / 1.3, which equals 500. This example introduces a scenario where we need to find the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 5 | Math Example--Percents--Equations with Percents: Example 5TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 30% of 9?" The solution involves converting 30% to its decimal form, 0.3, and then multiplying it by 9 to get the result of 2.7. This example introduces a larger percentage, demonstrating how the method applies consistently across various percentage values. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 6 | Math Example--Percents--Equations with Percents: Example 6TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 28% of 7.2?" The solution involves converting 28% to its decimal equivalent, 0.28, and then multiplying it by 7.2 to obtain the result of 2.016. This example combines a whole number percentage with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 7 | Math Example--Percents--Equations with Percents: Example 7TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 45% of 68?" The solution involves converting 45% to its decimal form, 0.45, and then multiplying it by 68 to arrive at the answer of 30.6. This example introduces a larger percentage and a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 8 | Math Example--Percents--Equations with Percents: Example 8TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 52.3% of 36.9?" The solution involves converting 52.3% to its decimal equivalent, 0.523, and then multiplying it by 36.9 to obtain the result of 19.2987. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation and showcasing the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |
|
Math Example--Percents--Equations with Percents: Example 9 | Math Example--Percents--Equations with Percents: Example 9TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 150% of 8?" The solution involves converting 150% to its decimal form, 1.5, and then multiplying it by 8 to get the result of 12. This example introduces a percentage greater than 100%, demonstrating how the method applies consistently even when dealing with percentages that represent values larger than the whole. |
Solving Percent Equations |
|
Math Example--Percents--Percent Change--Example 1 | Math Example--Percents--Percent Change--Example 1
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 10 | Math Example--Percents--Percent Change--Example 10
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 2 | Math Example--Percents--Percent Change--Example 2
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 3 | Math Example--Percents--Percent Change--Example 3
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 4 | Math Example--Percents--Percent Change--Example 4
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 5 | Math Example--Percents--Percent Change--Example 5
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 6 | Math Example--Percents--Percent Change--Example 6
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 7 | Math Example--Percents--Percent Change--Example 7
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 8 | Math Example--Percents--Percent Change--Example 8
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Percents--Percent Change--Example 9 | Math Example--Percents--Percent Change--Example 9
This is part of a collection of math examples that focus on percents. |
Percents |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 26 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 26
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 27 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 27
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 28 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 28
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 29 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 29
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
