Illustrative Math Alignment: Grade 7 Unit 5

Topic

Rational Functions

Topic

Rational Functions

Topic

Rational Functions

Description

Explains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety.

This video provides a detailed explanation of explains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety. and its significance in understanding rational functions.

Topic

Rational Functions

Description

Examines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates.

This video provides a detailed explanation of examines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates and its significance in understanding rational functions.

Topic

Rational Functions

Description

Demonstrates the optics of the Hubble telescope through rational functions, analyzing lens properties and asymptotes for image clarity.

This video provides a detailed explanation of demonstrates the optics of the Hubble telescope through rational functions, analyzing lens properties and asymptotes for image clarity and its significance in understanding rational functions.

After briefly reviewing the concept of inverse variation, this video explores Boyle’s law, a real world example of an inversely proportional relationship between pressure and volume of a gas. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, it goes on to examine similarities and differences among rational functions and numbers. Finally, it takes a look at rational functions graphs and ends with a delightful example merging Euclidean and analytic geometry, thanks to the TI-Nspire technology. Concepts explored: functions, rational expressions, rational functions, asymptotes

In this Investigation we look at an application of rational functions: Boyle's Law. This video is Segment 1 of a 4 segment series related to Algebra Nspirations: Rational Functions and Expressions. Segments 1 and 2 are grouped together.

In this Investigation we look at graphs of rational functions. This video is Segment 3 of a 4 segment series related to Algebra Nspirations: Rational Functions and Expressions. Segments 3 and 4 are grouped together.

In this TI Nspire tutorial, the Graph window is used to create a slider-based graph of a rational function. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. .

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

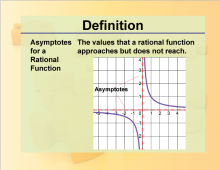
Topic

Rationals and Radicals

Definition

An asymptote is a line that a graph approaches but never touches.

Description

Asymptotes are significant in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of graphs of rational functions, particularly as the values of the variables approach certain limits. Horizontal asymptotes indicate the value that the function approaches as the input grows infinitely large or small. Vertical asymptotes show the values that the function cannot take because they cause division by zero.

Topic

Rationals and Radicals

Definition

The conjugate of a radical expression is obtained by changing the sign between two terms in a binomial.

Description

In the context of Radical Numbers, Expressions, Equations, and Functions, the concept of conjugates is essential for simplifying expressions. When dealing with radicals, particularly in the denominator, multiplying by the conjugate can help to rationalize the expression. This process eliminates the radical from the denominator, making the expression easier to work with.

Topic

Rationals and Radicals

Definition

The cube root of a number is a value that, when multiplied by itself three times, gives the original number.

Description

The cube root is a fundamental concept in Radical Numbers, Expressions, Equations, and Functions. It is the inverse operation of raising a number to the power of three. Understanding cube roots is crucial for solving equations involving cubic terms and for simplifying radical expressions.

Cube roots also appear in various real-world applications, such as calculating volumes and in certain physics equations. They are an integral part of higher-level mathematics, including algebra and calculus.

Topic

Rationals and Radicals

Definition

An extraneous solution is a solution derived from an equation that is not a valid solution to the original equation.

Description

Extraneous solutions often arise in the context of Rational and Radical Equations. They are solutions that appear during the process of solving an equation but do not satisfy the original equation. This can happen when both sides of an equation are squared or when other operations introduce additional solutions.

Topic

Rationals and Radicals

Definition

Factoring a radical involves expressing it as a product of simpler expressions.

Description

Factoring radicals is a key technique in the study of Radical Numbers, Expressions, Equations, and Functions. It simplifies complex radical expressions, making them easier to work with. This process is essential for solving equations and for performing algebraic manipulations involving radicals.

Understanding how to factor radicals is also important for simplifying expressions in calculus and higher-level mathematics. It helps in breaking down complex problems into more manageable parts.

Topic

Rationals and Radicals

Definition

The fourth root of a number is a value that, when raised to the power of four, gives the original number.

Description

The fourth root is an important concept in Radical Numbers, Expressions, Equations, and Functions. It is the inverse operation of raising a number to the power of four. Understanding fourth roots is crucial for solving higher-degree equations and for simplifying radical expressions.

Fourth roots are also relevant in various scientific and engineering applications where higher-degree roots are required. They are a part of advanced mathematical studies, including algebra and calculus.

Topic

Rationals and Radicals

Definition

The geometric mean of two numbers is the square root of their product.

Description

The geometric mean is an example of using radical expressions to solve a problem. It provides a measure of central tendency that is particularly useful in situations where the numbers are multiplied together rather than added.

In geometry, the geometric mean appears in various theorems and constructions. It is also used in finance and statistics to calculate average growth rates and to compare different sets of data.

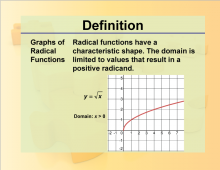
Topic

Rationals and Radicals

Definition

Graphs of radical functions are visual representations of equations involving radicals.

Description

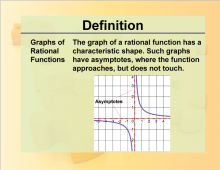
Graphs of radical functions are crucial in the study of Radical Numbers, Expressions, Equations, and Functions. They provide a visual understanding of how these functions behave, including their domains, ranges, and key features such as intercepts and asymptotes.

Topic

Rationals and Radicals

Definition

Graphs of rational functions are visual representations of equations involving rational expressions.

Description

Graphs of rational functions are fundamental in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of these functions, including their asymptotes, intercepts, and regions of increase and decrease.

Topic

Rationals and Radicals

Definition

A horizontal asymptote is a horizontal line that a rational function graph approaches as the input values become very large or very small.

Description

Horizontal asymptotes are an important concept in the study of Rational Numbers, Expressions, Equations, and Functions. They indicate the value that a function approaches as the input grows infinitely large or small. Understanding horizontal asymptotes is crucial for graphing rational functions accurately and for analyzing their long-term behavior.

Topic

Rationals and Radicals

Definition

Inverse variation describes a relationship between two variables in which the product is a constant. When one variable increases, the other decreases proportionally.

Topic

Rationals and Radicals

Definition

An irrational number is a number that cannot be expressed as a ratio of two integers. Its decimal form is non-repeating and non-terminating.

Topic

Rationals and Radicals

Definition

An irrational number is a number that cannot be expressed as a ratio of two integers. Its decimal form is non-repeating and non-terminating.

Topic

Rationals and Radicals

Definition

The laws of rational exponents describe how to handle exponents that are fractions, including rules for multiplication, division, and raising a power to a power.

Description

The Laws of Rational Exponents are vital in the study of Rational Numbers, Expressions, Equations, and Functions. These laws provide a framework for simplifying expressions involving exponents that are fractions. For example, the law

 $$a^{m/n} = \sqrt[n]{a^m}$$ 

Topic

Rationals and Radicals

Definition

The nth root of a number is a value that, when raised to the power of n, gives the original number. It is denoted as $$\sqrt[n]{a}$$

Description

The nth Root is a fundamental concept in the study of Radical Numbers, Expressions, Equations, and Functions. It generalizes the idea of square roots and cube roots to any positive integer n. For example, the cube root of 8 is 2 because 

$$2^3 = 8$$

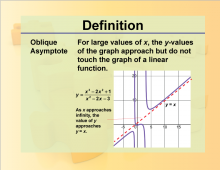
Topic

Rationals and Radicals

Definition

An oblique asymptote is a diagonal line that the graph of a function approaches as the input values become very large or very small.

Description

Oblique Asymptotes are important in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions where the degree of the numerator is one more than the degree of the denominator. For example, the function 

$$f(x) = \frac{x^2 + 1}{x}$$

Topic

Rationals and Radicals

Definition

Partial fraction decomposition is a method used to express a rational expression as a sum of simpler fractions.

Description

Partial Fraction Decomposition is a powerful tool in the study of Rational Numbers, Expressions, Equations, and Functions. It involves breaking down a complex rational expression into a sum of simpler fractions, which are easier to integrate or differentiate. For example, the rational function 

$$\frac{2x+3}{(x+1)(x-2)}$$

can be decomposed into 

Topic

Rationals and Radicals

Definition

Radical equations are equations in which the variable is inside a radical, such as a square root or cube root.

Description

Radical Equations are a fundamental aspect of Radical Numbers, Expressions, Equations, and Functions. These equations involve variables within radical signs, such as square roots or cube roots. Solving radical equations typically requires isolating the radical on one side of the equation and then squaring both sides to eliminate the radical. For example, to solve 

$$\sqrt{x+3} = 5$$

one would square both sides to obtain 

$$x + 3 = 25$$

Topic

Rationals and Radicals

Definition

A radical expression is an expression that contains a radical symbol, which indicates the root of a number.

Description

Radical Expressions are a core component of Radical Numbers, Expressions, Equations, and Functions. These expressions involve roots, such as square roots, cube roots, or higher-order roots, and are denoted by the radical symbol (√). For example, the expression 

$$\sqrt{16}$$ 

Topic

Rationals and Radicals

Definition

A radical function is a function that contains a radical expression with the independent variable in the radicand.

Description

Radical Functions are a vital part of Radical Numbers, Expressions, Equations, and Functions. These functions involve radicals, such as square roots or cube roots, with the independent variable inside the radical. For example, the function

$$f(x) = \sqrt{x}$$

Topic

Rationals and Radicals

Definition

The radical symbol (√) is used to denote the root of a number, such as a square root or cube root.

Description

The Radical Symbol is a fundamental notation in the study of Radical Numbers, Expressions, Equations, and Functions. This symbol (√) indicates the root of a number, with the most common being the square root. For example, the expression 

$$\sqrt{25}$$

Topic

Rationals and Radicals

Definition

The radicand is the number or expression inside the radical symbol that is being rooted.

Description

The Radicand is a key component in the study of Radical Numbers, Expressions, Equations, and Functions. It is the number or expression inside the radical symbol that is being rooted. For example, in the expression 

$$\sqrt{49}$$

Topic

Rationals and Radicals

Definition

Rational equations are equations that involve rational expressions, which are fractions containing polynomials in the numerator and denominator.

Description

Rational Equations are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These equations involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Solving rational equations typically requires finding a common denominator, clearing the fractions, and then solving the resulting polynomial equation. For example, to solve 

$$\frac{1}{x} + \frac{1}{x+1} = \frac{1}{2}$$

Topic

Rationals and Radicals

Definition

A rational exponent is an exponent that is a fraction, where the numerator indicates the power and the denominator indicates the root.

Description

Rational Exponents are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. These exponents are fractions, where the numerator indicates the power and the denominator indicates the root. For example, the expression 

$$a^{m/n}$$

can be rewritten as 

$$\sqrt[n]{a^m}$$

Topic

Rationals and Radicals

Definition

Rational expressions are fractions in which the numerator and/or the denominator are polynomials.

Description

Rational Expressions are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These expressions are fractions where the numerator and/or the denominator are polynomials. Simplifying rational expressions often involves factoring the polynomials and canceling common factors. For example, the rational expression 

$$\frac{x^2 - 1}{x - 1}$$

can be simplified to x + 1, provided that 

$$x \neq 1$$

Topic

Rationals and Radicals

Definition

Rational functions are functions that are the ratio of two polynomials.

Description

Rational Functions are a key concept in the study of Rational Numbers, Expressions, Equations, and Functions. These functions are the ratio of two polynomials, such as 

$$f(x) = \frac{P(x)}{Q(x)}$$

where P(x) and Q(x) are polynomials. Understanding rational functions involves analyzing their behavior, including identifying asymptotes, intercepts, and discontinuities. For example, the function 

$$f(x) = \frac{1}{x}$$

Topic

Rationals and Radicals

Definition

Rational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero.

Topic

Rationals and Radicals

Definition

Rationalizing a radical is the process of eliminating radicals from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor.

Description

Rationalizing a Radical is an important technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves eliminating radicals from the denominator of a fraction, which simplifies the expression and often makes it easier to work with or compare to other expressions. For example, to rationalize the denominator of 

$$\frac{1}{\sqrt{3}}$$