
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 10: Different Options for Solving One Equation
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
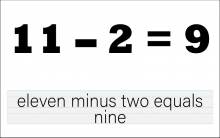
|
Math Clip Art--The Language of Math--Numbers and Equations 26 | Math Clip Art--The Language of Math--Numbers and Equations 26TopicThe Language of Math DescriptionThis clip art from the Language of Math collection showcases the equation "11-2=9" in both numerical and word formats. It continues the progression of subtraction concepts, now working with larger two-digit numbers. The simultaneous presentation of the equation in symbols and words reinforces the connection between mathematical language and everyday language. This visual representation helps students understand how subtraction works with larger numbers and introduces the concept of "finding the difference" between two numbers. |
Numerical Expressions |
|
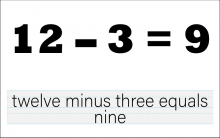
Math Clip Art--The Language of Math--Numbers and Equations 27 | Math Clip Art--The Language of Math--Numbers and Equations 27TopicThe Language of Math DescriptionThis image presents the equation "12-3=9" in both numerical and word form. It advances the complexity of subtraction concepts by introducing larger two-digit numbers and a subtrahend greater than 1. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of subtraction, particularly how removing multiple units from a quantity affects the result. |
Numerical Expressions |
|
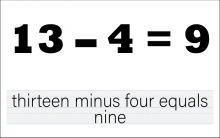
Math Clip Art--The Language of Math--Numbers and Equations 28 | Math Clip Art--The Language of Math--Numbers and Equations 28TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "13-4=9" in both numerical and word form. It continues the progression of subtraction concepts, now working with larger two-digit numbers and a subtrahend greater than 3. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how subtraction works with larger numbers and reinforces the concept of "finding the difference" between two numbers. |
Numerical Expressions |
|
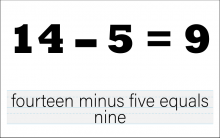
Math Clip Art--The Language of Math--Numbers and Equations 29 | Math Clip Art--The Language of Math--Numbers and Equations 29TopicThe Language of Math DescriptionThis image presents the equation "14-5=9" in both numerical and word form. It advances the complexity of subtraction concepts by introducing larger two-digit numbers and a subtrahend of 5. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of subtraction, particularly how removing half of 10 from a teen number results in a single-digit answer. |
Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Equations 30 | Math Clip Art--The Language of Math--Numbers and Equations 30TopicThe Language of Math DescriptionThis clip art from the Language of Math collection showcases the equation "15-6=9" in both numerical and word formats. It continues the progression of subtraction concepts, now working with larger two-digit numbers and a subtrahend greater than 5. |
Numerical Expressions |
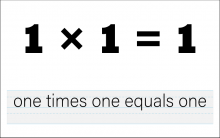
|
Math Clip Art--The Language of Math--Numbers and Equations 31 | Math Clip Art--The Language of Math--Numbers and Equations 31TopicThe Language of Math DescriptionThis image illustrates the equation "1*1=1" in both numerical and word form. It introduces the concept of multiplication, starting with the simplest case of multiplying 1 by itself. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication as repeated addition. |
Numerical Expressions |
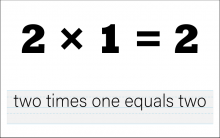
|
Math Clip Art--The Language of Math--Numbers and Equations 32 | Math Clip Art--The Language of Math--Numbers and Equations 32TopicThe Language of Math DescriptionThis clip art from the Language of Math collection showcases the equation "2*1=2" in both numerical and word formats. It continues the introduction of multiplication concepts, now showing multiplication by 1. The simultaneous presentation of the equation in symbols and words reinforces the connection between mathematical language and everyday language. This visual representation helps students understand how multiplication works and introduces the concept of the identity property of multiplication. |
Numerical Expressions |
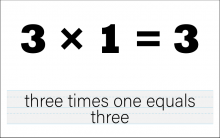
|
Math Clip Art--The Language of Math--Numbers and Equations 33 | Math Clip Art--The Language of Math--Numbers and Equations 33TopicThe Language of Math DescriptionThis image presents the equation "3*1=3" in both numerical and word form. It continues the progression of multiplication concepts, focusing on the multiplication of a single-digit number by 1. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication, particularly how multiplying by 1 results in the same number. |
Numerical Expressions |
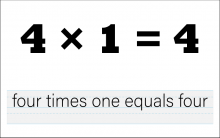
|
Math Clip Art--The Language of Math--Numbers and Equations 34 | Math Clip Art--The Language of Math--Numbers and Equations 34TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "4*1=4" in both numerical and word form. It continues the progression of multiplication concepts, focusing on the multiplication of a single-digit number by 1. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how multiplication works and reinforces the concept of the identity property of multiplication. |
Numerical Expressions |
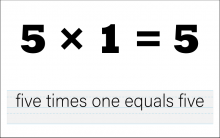
|
Math Clip Art--The Language of Math--Numbers and Equations 35 | Math Clip Art--The Language of Math--Numbers and Equations 35TopicThe Language of Math DescriptionThis image presents the equation "5*1=5" in both numerical and word form. It continues the progression of multiplication concepts, focusing on the multiplication of a single-digit number by 1. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication, particularly how multiplying by 1 results in the same number. |
Numerical Expressions |
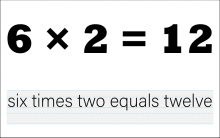
|
Math Clip Art--The Language of Math--Numbers and Equations 36 | Math Clip Art--The Language of Math--Numbers and Equations 36TopicThe Language of Math DescriptionThis clip art from the Language of Math collection showcases the equation "6*2=12" in both numerical and word formats. It advances the complexity of multiplication concepts by introducing multiplication by a number other than 1. The simultaneous presentation of the equation in symbols and words reinforces the connection between mathematical language and everyday language. This visual representation helps students understand how multiplication works with larger numbers and introduces the concept of repeated addition. |
Numerical Expressions |
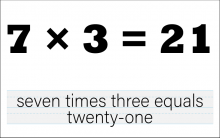
|
Math Clip Art--The Language of Math--Numbers and Equations 37 | Math Clip Art--The Language of Math--Numbers and Equations 37TopicThe Language of Math DescriptionThis image presents the equation "7*3=21" in both numerical and word form. It continues the progression of multiplication concepts, now introducing multiplication with larger single-digit numbers. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication, particularly how it relates to repeated addition and grouping. |
Numerical Expressions |
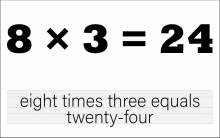
|
Math Clip Art--The Language of Math--Numbers and Equations 38 | Math Clip Art--The Language of Math--Numbers and Equations 38TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "8*3=24" in both numerical and word form. It continues the progression of multiplication concepts, focusing on multiplication with larger single-digit numbers. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how multiplication works with larger numbers and reinforces the concept of repeated addition and grouping. |
Numerical Expressions |
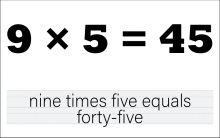
|
Math Clip Art--The Language of Math--Numbers and Equations 39 | Math Clip Art--The Language of Math--Numbers and Equations 39TopicThe Language of Math DescriptionThis image presents the equation "9*5=45" in both numerical and word form. It advances the complexity of multiplication concepts by introducing larger single-digit numbers and a product greater than 40. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication, particularly how it relates to repeated addition and grouping with larger numbers. |
Numerical Expressions |
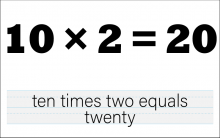
|
Math Clip Art--The Language of Math--Numbers and Equations 40 | Math Clip Art--The Language of Math--Numbers and Equations 40TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "10*2=20" in both numerical and word form. It introduces multiplication with a two-digit number, marking a significant step in mathematical understanding. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how multiplication works with larger numbers and reinforces the concept of repeated addition and grouping. |
Numerical Expressions |
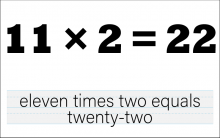
|
Math Clip Art--The Language of Math--Numbers and Equations 41 | Math Clip Art--The Language of Math--Numbers and Equations 41TopicThe Language of Math DescriptionThis image presents the equation "11*2=22" in both numerical and word form. It continues the progression of multiplication concepts, now working with two-digit numbers. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication, particularly how it relates to repeated addition and grouping with larger numbers. |
Numerical Expressions |
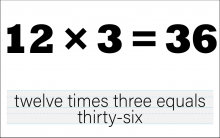
|
Math Clip Art--The Language of Math--Numbers and Equations 42 | Math Clip Art--The Language of Math--Numbers and Equations 42TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "12*3=36" in both numerical and word form. It advances the complexity of multiplication concepts by introducing larger two-digit numbers and a product greater than 30. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how multiplication works with larger numbers and reinforces the concept of repeated addition and grouping. |
Numerical Expressions |
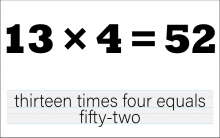
|
Math Clip Art--The Language of Math--Numbers and Equations 43 | Math Clip Art--The Language of Math--Numbers and Equations 43TopicThe Language of Math DescriptionThis image presents the equation "13*4=52" in both numerical and word form. It continues the progression of multiplication concepts, now working with larger two-digit numbers and a product greater than 50. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication, particularly how it relates to repeated addition and grouping with larger numbers. |
Numerical Expressions |
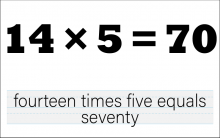
|
Math Clip Art--The Language of Math--Numbers and Equations 44 | Math Clip Art--The Language of Math--Numbers and Equations 44TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "14*5=70" in both numerical and word form. It advances the complexity of multiplication concepts by introducing larger two-digit numbers and a product reaching 70. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how multiplication works with larger numbers and reinforces the concept of repeated addition and grouping. |
Numerical Expressions |
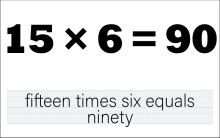
|
Math Clip Art--The Language of Math--Numbers and Equations 45 | Math Clip Art--The Language of Math--Numbers and Equations 45TopicThe Language of Math DescriptionThis image presents the equation "15*6=90" in both numerical and word form. It continues the progression of multiplication concepts, now working with larger two-digit numbers and a product reaching 90. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of multiplication, particularly how it relates to repeated addition and grouping with larger numbers. |
Numerical Expressions |
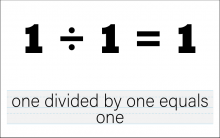
|
Math Clip Art--The Language of Math--Numbers and Equations 46 | Math Clip Art--The Language of Math--Numbers and Equations 46TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "1/1=1" in both numerical and word form. It introduces the concept of division, starting with the simplest case of dividing a number by itself. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand the basic concept of division and introduces the idea that any number divided by itself equals 1. |
Numerical Expressions |
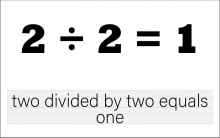
|
Math Clip Art--The Language of Math--Numbers and Equations 47 | Math Clip Art--The Language of Math--Numbers and Equations 47TopicThe Language of Math DescriptionThis image presents the equation "2/2=1" in both numerical and word form. It continues the progression of division concepts, now working with a fraction where the numerator and denominator are equal. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of division, particularly how dividing a number by itself always results in 1. |
Numerical Expressions |
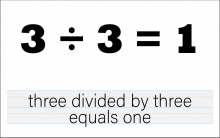
|
Math Clip Art--The Language of Math--Numbers and Equations 48 | Math Clip Art--The Language of Math--Numbers and Equations 48TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "3/3=1" in both numerical and word form. It continues the series of division concepts, focusing on fractions where the numerator and denominator are equal. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how division works and reinforces the concept that any number divided by itself equals 1. |
Numerical Expressions |
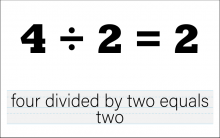
|
Math Clip Art--The Language of Math--Numbers and Equations 49 | Math Clip Art--The Language of Math--Numbers and Equations 49TopicThe Language of Math DescriptionThis image presents the equation "4/2=2" in both numerical and word form. It advances the complexity of division concepts by introducing a fraction where the numerator is greater than the denominator. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of division, particularly how dividing by a smaller number results in a larger quotient. |
Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Equations 50 | Math Clip Art--The Language of Math--Numbers and Equations 50TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "5/1=5" in both numerical and word form. It introduces the concept of dividing by 1, which is a fundamental principle in mathematics. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand that dividing a number by 1 results in the same number, reinforcing the identity property of division. |
Numerical Expressions |
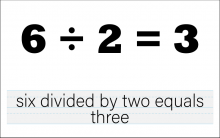
|
Math Clip Art--The Language of Math--Numbers and Equations 51 | Math Clip Art--The Language of Math--Numbers and Equations 51TopicThe Language of Math DescriptionThis image presents the equation "6/2=3" in both numerical and word form. It continues the progression of division concepts, now working with larger numbers and introducing the concept of halving. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of division, particularly how dividing by 2 relates to finding half of a number. |
Numerical Expressions |
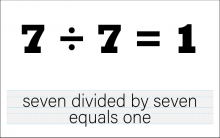
|
Math Clip Art--The Language of Math--Numbers and Equations 52 | Math Clip Art--The Language of Math--Numbers and Equations 52TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "7/7=1" in both numerical and word form. It reinforces the concept that any number divided by itself equals 1. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand a fundamental principle of division and introduces the concept of equivalent fractions. |
Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Equations 53 | Math Clip Art--The Language of Math--Numbers and Equations 53TopicThe Language of Math DescriptionThis image presents the equation "8/4=2" in both numerical and word form. It advances the complexity of division concepts by introducing division with larger numbers and the concept of quartering. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of division, particularly how dividing by 4 relates to finding a quarter of a number. |
Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Equations 54 | Math Clip Art--The Language of Math--Numbers and Equations 54TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "9/3=3" in both numerical and word form. It continues the progression of division concepts, now working with larger numbers and introducing the concept of thirds. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how division works with larger numbers and reinforces the concept of equal sharing. |
Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Equations 55 | Math Clip Art--The Language of Math--Numbers and Equations 55TopicThe Language of Math DescriptionThis image presents the equation "10/2=5" in both numerical and word form. It continues the progression of division concepts, now working with larger numbers and reinforcing the concept of halving. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of division, particularly how dividing by 2 relates to finding half of a number, even with larger values. |
Numerical Expressions |
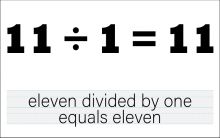
|
Math Clip Art--The Language of Math--Numbers and Equations 56 | Math Clip Art--The Language of Math--Numbers and Equations 56TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "11/1=11" in both numerical and word form. It introduces the concept of dividing by 1, which is a fundamental principle in mathematics. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand that dividing a number by 1 results in the same number, reinforcing the identity property of division. |
Numerical Expressions |
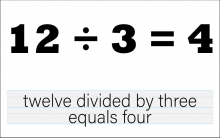
|
Math Clip Art--The Language of Math--Numbers and Equations 57 | Math Clip Art--The Language of Math--Numbers and Equations 57TopicThe Language of Math DescriptionThis image presents the equation "12/3=4" in both numerical and word form. It advances the complexity of division concepts by working with larger numbers and introducing the concept of dividing by 3. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of division, particularly how dividing by 3 relates to grouping numbers into thirds. |
Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Equations 58 | Math Clip Art--The Language of Math--Numbers and Equations 58TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "13/13=1" in both numerical and word form. It reinforces the concept that any number divided by itself equals 1, now using a larger number. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand a fundamental principle of division and introduces the concept of equivalent fractions with larger numbers. |
Numerical Expressions |
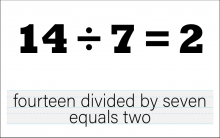
|
Math Clip Art--The Language of Math--Numbers and Equations 59 | Math Clip Art--The Language of Math--Numbers and Equations 59TopicThe Language of Math DescriptionThis image presents the equation "14/7=2" in both numerical and word form. It continues the progression of division concepts, now working with larger numbers and introducing the concept of halving with two-digit numbers. The dual representation of the equation reinforces the connection between mathematical symbols and their verbal expressions. This visual aid is crucial in developing number sense and understanding the concept of division, particularly how dividing by half of a number results in 2. |
Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Equations 60 | Math Clip Art--The Language of Math--Numbers and Equations 60TopicThe Language of Math DescriptionThis clip art from the Language of Math collection illustrates the equation "15/3=5" in both numerical and word form. It advances the complexity of division concepts by working with larger numbers and introducing the concept of dividing by 3. The simultaneous presentation of the equation in symbols and words strengthens the connection between mathematical language and everyday language. This visual representation helps students understand how division works with larger numbers and reinforces the concept of grouping into thirds. |
Numerical Expressions |
|
Math Clip Art--The Language of Math--Numbers and Equations 61 | Math Clip Art--The Language of Math--Numbers and Equations 61TopicThe Language of Math DescriptionThis image presents a blank card, serving as the final piece in the series of 61 clip art images focused on the Language of Math: Numbers and Equations. While it doesn't contain a specific equation, its presence is significant in the collection. |
Numerical Expressions |
|
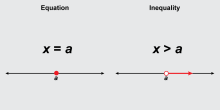
Math Clip Art: Equations vs. Inequalities | Math Clip Art: Equations vs. Inequalities This collection of clip art images show the contrast between graphs of equations and inequalities for one- and two-variable graphs. |
Inequalities |

|
Math Clip Art: Solving Equations and Inequalities | Math Clip Art: Solving Equations and Inequalities Use these clip art images to show how to solve linear equations and inequalities. Examples include situations where the inequality symbol changes. |
Inequalities |
|
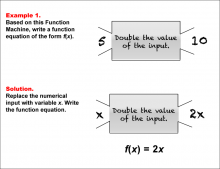
Math Example--Function Concepts--Function Rules and Equations--Example 1 | Math Example--Function Concepts--Function Rules and Equations--Example 1TopicArithmetic DescriptionExample 1: Write a function equation of the form f(x) based on the Function Machine that takes an input and doubles its value. The input shown is 5, and the output is 10. To find the solution, replace the numerical input with the variable x. Since the machine doubles the input, the function equation is f(x) = 2x. |
Relations and Functions |
|
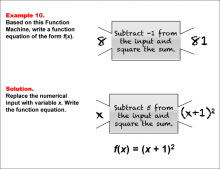
Math Example--Function Concepts--Function Rules and Equations--Example 10 | Math Example--Function Concepts--Function Rules and Equations--Example 10TopicArithmetic DescriptionExample 10: Write a function equation of the form f(x) based on the Function Machine that subtracts -1 (or adds 1) from the input and squares the sum. The input is 8, and the output is 81. Substitute x for the input. The machine subtracts -1 from x (equivalent to adding 1) and squares the result, so the function equation is f(x) = (x + 1)2. |
Relations and Functions |
|
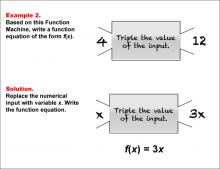
Math Example--Function Concepts--Function Rules and Equations--Example 2 | Math Example--Function Concepts--Function Rules and Equations--Example 2TopicArithmetic DescriptionExample 2: Write a function equation of the form f(x) based on the Function Machine that takes an input and triples its value. The input shown is 4, and the output is 12. By replacing the numerical input with the variable x and applying the machine's rule to triple the input, the function equation is f(x) = 3x. |
Relations and Functions |
|
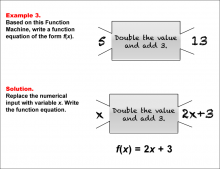
Math Example--Function Concepts--Function Rules and Equations--Example 3 | Math Example--Function Concepts--Function Rules and Equations--Example 3TopicArithmetic DescriptionExample 3: Write a function equation of the form f(x) based on the Function Machine that doubles the value of the input and then adds 3. The input is 5, and the output is 13. To determine the function, replace the input with x. The machine doubles the input and then adds 3, so the function equation is f(x) = 2x + 3. |
Relations and Functions |
|
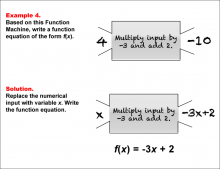
Math Example--Function Concepts--Function Rules and Equations--Example 4 | Math Example--Function Concepts--Function Rules and Equations--Example 4TopicArithmetic DescriptionEΘample 4: Write a function equation of the form f(Θ) based on the Function Machine that multiplies the input by -3 and then adds 2. The input is 4, and the output is -10. Substitute the numerical input with x. Since the machine multiplies the input by -3 and adds 2, the function equation is f(x) = -3x + 2. |
Relations and Functions |
|
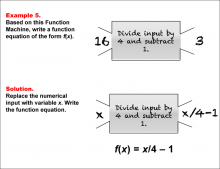
Math Example--Function Concepts--Function Rules and Equations--Example 5 | Math Example--Function Concepts--Function Rules and Equations--Example 5TopicArithmetic DescriptionExample 5: Write a function equation of the form f(x) based on the Function Machine that divides the input by 4 and then subtracts 1. The input shown is 16, and the output is 3. Replace the input with x. Applying the function machine's rule to divide by 4 and subtract 1, the function equation is f(x) = x / 4 - 1. |
Relations and Functions |
|
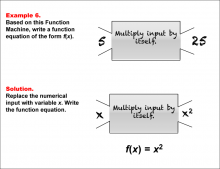
Math Example--Function Concepts--Function Rules and Equations--Example 6 | Math Example--Function Concepts--Function Rules and Equations--Example 6TopicArithmetic DescriptionExample 6: Write a function equation of the form f(x) based on the Function Machine that multiplies the input by itself (squares it). The input is 5, and the output is 25. Substitute the input with x. Since the machine squares the input, the function equation is f(x) = x2. |
Relations and Functions |
|
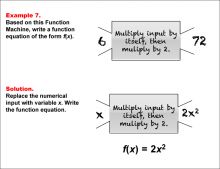
Math Example--Function Concepts--Function Rules and Equations--Example 7 | Math Example--Function Concepts--Function Rules and Equations--Example 7TopicArithmetic DescriptionExample 7: Write a function equation of the form f(x) based on the Function Machine that multiplies the input by itself and then multiplies the result by 2. The input is 6, and the output is 72. Replace the input with x. The machine squares the input and then multiplies it by 2, so the function equation is f(x) = 2x2. |
Relations and Functions |
|
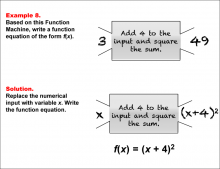
Math Example--Function Concepts--Function Rules and Equations--Example 8 | Math Example--Function Concepts--Function Rules and Equations--Example 8TopicArithmetic DescriptionExample 8: Write a function equation of the form f(x) based on the Function Machine that adds 4 to the input and then squares the sum. The input is 3, and the output is 49. Substitute x for the input. The machine adds 4 to x and then squares the result, giving the function equation f(x) = (x + 4)2. |
Relations and Functions |
|
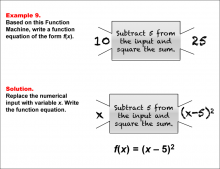
Math Example--Function Concepts--Function Rules and Equations--Example 9 | Math Example--Function Concepts--Function Rules and Equations--Example 9TopicArithmetic DescriptionExample 9: Write a function equation of the form f(x) based on the Function Machine that subtracts 5 from the input and then squares the sum. The input is 10, and the output is 25. Replace the input with x. Since the machine subtracts 5 from x and squares the result, the function equation is f(x) = (x - 5)2. |
Relations and Functions |
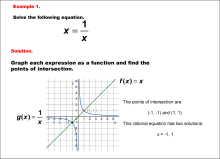
|
Math Example--Graphical Solutions to Rational Equations--Example 1 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
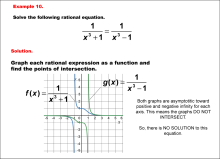
|
Math Example--Graphical Solutions to Rational Equations--Example 10 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |