
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 10: Different Options for Solving One Equation
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Percents--Equations with Percents: Example 9 | Math Example--Percents--Equations with Percents: Example 9TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 150% of 8?" The solution involves converting 150% to its decimal form, 1.5, and then multiplying it by 8 to get the result of 12. This example introduces a percentage greater than 100%, demonstrating how the method applies consistently even when dealing with percentages that represent values larger than the whole. |
Solving Percent Equations |
|
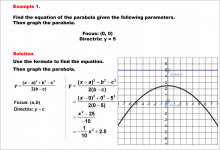
Math Example--Quadratics--Equations of Parabolas--Example 1 | Equations of Parabolas--Example 1TopicQuadratics DescriptionIn this example, we're given a parabola with its focus at (0, 0) and directrix y = 5. Using the locus definition, we can determine that the vertex is at (0, 2.5), halfway between the focus and directrix. The distance p from the vertex to the focus is 2.5. This example demonstrates how the focus and directrix directly determine the equation of the parabola. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions |
|
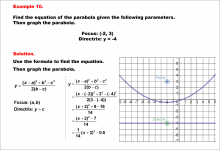
Math Example--Quadratics--Equations of Parabolas--Example 10 | Equations of Parabolas--Example 10TopicQuadratics |
Graphs of Quadratic Functions |
|
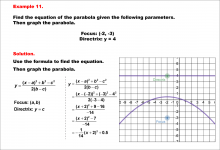
Math Example--Quadratics--Equations of Parabolas--Example 11 | Equations of Parabolas--Example 11TopicQuadratics |
Graphs of Quadratic Functions |
|
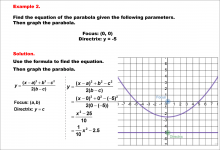
Math Example--Quadratics--Equations of Parabolas--Example 2 | Equations of Parabolas--Example 2TopicQuadratics DescriptionThis example presents a parabola with its focus at (0, 0) and directrix x = -4. The vertex is at (0, -2.5), midway between the focus and directrix. The distance p from the vertex to the focus is 2.5. This example illustrates how a vertically-oriented parabola's equation is derived from its focus and directrix. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions |
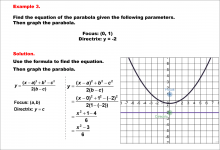
|
Math Example--Quadratics--Equations of Parabolas--Example 3 | Equations of Parabolas--Example 3TopicQuadratics DescriptionIn this example, the parabola has its focus at (0, 1) and directrix y = -2. The vertex is at (0, -0.5), and the parabola opens upward. The distance p from the vertex to the focus is 1.5. This example reinforces the relationship between the focus, directrix, and the resulting equation of the parabola. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions |
|
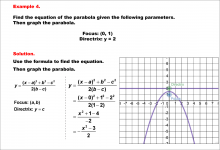
Math Example--Quadratics--Equations of Parabolas--Example 4 | Equations of Parabolas--Example 4TopicQuadratics DescriptionThis example shows a parabola with its focus at (0, 1) and directrix y = 2. The parabola opens downward with its vertex at (0, 1.5). The distance p from the vertex to the focus is 0.5. This example illustrates how the position of the focus and directrix determines the orientation and equation of the parabola. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions |
|
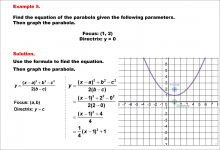
Math Example--Quadratics--Equations of Parabolas--Example 5 | Equations of Parabolas--Example 5TopicQuadratics DescriptionIn this example, the parabola has its focus at (1, 2) and directrix y = 0. The vertex is at (1, 1), and the parabola opens upward. The distance p from the vertex to the focus is 1. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions |
|
Math Example--Quadratics--Equations of Parabolas--Example 6 | Equations of Parabolas--Example 6TopicQuadratics |
Graphs of Quadratic Functions |
|
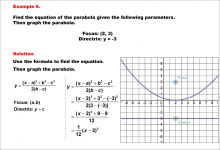
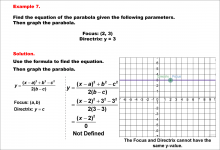
Math Example--Quadratics--Equations of Parabolas--Example 7 | Equations of Parabolas--Example 7TopicQuadratics DescriptionThis example presents a parabola with its focus at (2, 3) and directrix y = 3. This parabola is not defined because the focus and directrix cannot have the same y-value. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions |
|
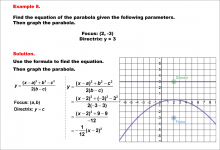
Math Example--Quadratics--Equations of Parabolas--Example 8 | Equations of Parabolas--Example 8TopicQuadratics |
Graphs of Quadratic Functions |
|
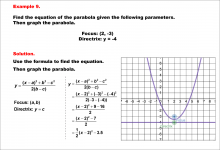
Math Example--Quadratics--Equations of Parabolas--Example 9 | Equations of Parabolas--Example 9TopicQuadratics |
Graphs of Quadratic Functions |
|
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 1 | Graphical Solutions to Quadratic Equations: Example 1TopicQuadratics |
Quadratic Equations and Functions |
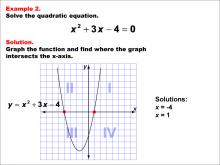
|
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 2 | Graphical Solutions to Quadratic Equations: Example 2TopicQuadratics |
Quadratic Equations and Functions |
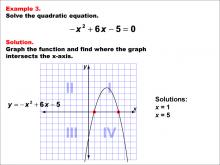
|
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 3 | Graphical Solutions to Quadratic Equations: Example 3TopicQuadratics |
Quadratic Equations and Functions |
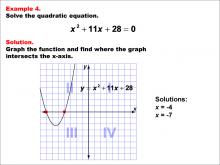
|
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 4 | Graphical Solutions to Quadratic Equations: Example 4TopicQuadratics DescriptionThis example illustrates a parabola intersecting the x-axis at two distinct points, indicating two real and distinct solutions. The graph provides a visual representation of the roots and helps in understanding the impact of the quadratic equation's coefficients on the shape and position of the parabola. Graphical solutions are advantageous for quickly identifying the number of solutions, but they may not offer precise numerical solutions without additional calculations. |
Quadratic Equations and Functions |
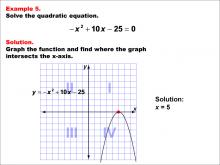
|
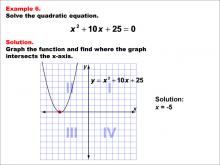
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 5 | Graphical Solutions to Quadratic Equations: Example 5TopicQuadratics DescriptionThis example shows a parabola that is tangent to the x-axis, indicating a single real solution. This scenario occurs when the quadratic equation has a perfect square trinomial, resulting in a discriminant of zero. The graphical approach provides an intuitive understanding of why there is only one solution. However, it may not be sufficient for finding the exact solution without algebraic methods, especially if the vertex is not at a simple coordinate. |
Quadratic Equations and Functions |
|
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 6 | Graphical Solutions to Quadratic Equations: Example 6TopicQuadratics DescriptionThis example shows a parabola that is tangent to the x-axis, indicating a single real solution. This scenario occurs when the quadratic equation has a perfect square trinomial, resulting in a discriminant of zero. The graphical approach provides an intuitive understanding of why there is only one solution. However, it may not be sufficient for finding the exact solution without algebraic methods, especially if the vertex is not at a simple coordinate. |
Quadratic Equations and Functions |
|
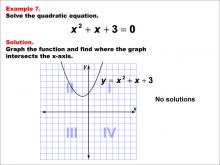
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 7 | Graphical Solutions to Quadratic Equations: Example 7TopicQuadratics DescriptionThis example illustrates a quadratic graph with no x-intercepts, indicating no real solutions. The graph provides a straightforward way to see where the solutions lie on the x-axis. This method is particularly advantageous for visual learners and for gaining a conceptual understanding of the roots. However, it may not always provide precise solutions, especially if the intercepts are not integers or easily readable from the graph. |
Quadratic Equations and Functions |
|
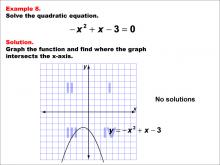
Math Example--Quadratics--Graphical Solutions to Quadratic Equations: Example 8 | Graphical Solutions to Quadratic Equations: Example 8TopicQuadratics DescriptionThis example shows a parabola not intersecting the x-axis, indicating no real solutions. The graph helps in visualizing the solutions and understanding how the quadratic equation's coefficients affect the graph's orientation and position. Graphical solutions are beneficial for quickly identifying the nature of the solutions, but they may not provide exact numerical answers without further analytical work. |
Quadratic Equations and Functions |
|
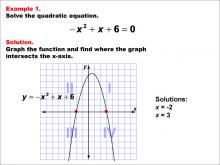
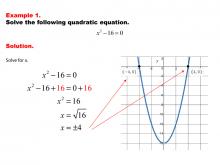
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 1 | Solving Simple Quadratic Equations--Example 1TopicQuadratics DescriptionThis example demonstrates solving a simplified form of a quadratic equation. The equation is in the form ax² = c, where the linear term (bx) is absent. This simplification allows for a straightforward solution by isolating x² and then taking the square root of both sides. The process is more direct than using the quadratic formula, making it easier to solve mentally or with minimal calculations. This method highlights the importance of recognizing special forms of quadratic equations for efficient problem-solving. |
Quadratic Equations and Functions |
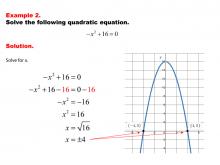
|
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 2 | Solving Simple Quadratic Equations--Example 2TopicQuadratics DescriptionThis example showcases another simplified quadratic equation. The equation is in a form where factoring or using the square root method is straightforward. By recognizing this simpler structure, students can solve the equation without resorting to more complex techniques. This approach emphasizes the importance of identifying the most efficient method based on the equation's form, promoting problem-solving skills and mathematical intuition. |
Quadratic Equations and Functions |
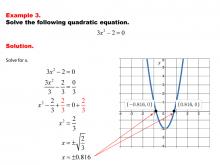
|
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 3 | Solving Simple Quadratic Equations--Example 3TopicQuadratics DescriptionIn this example, the quadratic equation is presented in a simplified form that allows for direct solving. The structure of the equation makes it possible to solve without using the quadratic formula or complex factoring techniques. This straightforward approach highlights how recognizing certain forms of quadratic equations can lead to quicker and more intuitive solutions, enhancing problem-solving efficiency. |
Quadratic Equations and Functions |
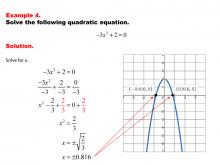
|
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 4 | Solving Simple Quadratic Equations--Example 4TopicQuadratics DescriptionThis example illustrates solving a quadratic equation in a simplified form. The equation's structure allows for a direct solution method, avoiding the need for more complex techniques like the quadratic formula. By recognizing this simpler form, students can apply basic algebraic skills to solve the equation efficiently, reinforcing the importance of identifying the most appropriate solving method based on the equation's characteristics. |
Quadratic Equations and Functions |
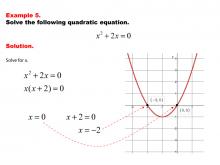
|
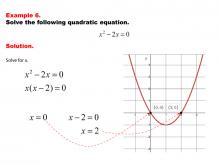
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 5 | Solving Simple Quadratic Equations--Example 5TopicQuadratics DescriptionThis example demonstrates solving a quadratic equation in a simplified form that allows for straightforward solution methods. The equation's structure enables direct solving techniques, bypassing the need for more complex approaches. This simplified form emphasizes the importance of recognizing patterns in quadratic equations, allowing for more efficient problem-solving and deepening understanding of quadratic relationships. |
Quadratic Equations and Functions |
|
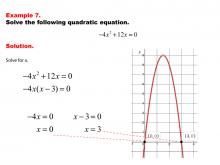
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 6 | Solving Simple Quadratic Equations--Example 6TopicQuadratics DescriptionIn this example, a simplified form of a quadratic equation is presented, allowing for a more direct solving approach. The equation's structure makes it possible to apply basic algebraic techniques without resorting to complex methods. This straightforward solution process highlights the importance of recognizing special forms of quadratic equations, enabling students to choose the most efficient solving strategy. |
Quadratic Equations and Functions |
|
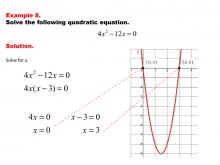
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 7 | Solving Simple Quadratic Equations--Example 7TopicQuadratics DescriptionThis example showcases solving a quadratic equation in a simplified form that allows for direct solution methods. The equation's structure enables the use of basic algebraic techniques, avoiding the need for more complex approaches like the quadratic formula. This simplified approach emphasizes the importance of identifying the most efficient solving method based on the equation's form, enhancing problem-solving skills and mathematical intuition. |
Quadratic Equations and Functions |
|
Math Example--Quadratics--Solving Simple Quadratic Equations--Example 8 | Solving Simple Quadratic Equations--Example 8TopicQuadratics DescriptionIn this final example, a simplified quadratic equation is presented, demonstrating how certain forms allow for straightforward solving techniques. The equation's structure enables direct solution methods, bypassing the need for complex approaches. This example reinforces the importance of recognizing special forms of quadratic equations, allowing students to apply the most efficient solving strategy and deepen their understanding of quadratic relationships. |
Quadratic Equations and Functions |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 1 | Equations Using the Exterior Angle Theorem--Example 1TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 10 | Equations Using the Exterior Angle Theorem--Example 10TopicEquations DescriptionThis example illustrates a more complex application of the Exterior Angle Theorem in solving triangle-related equations. In this scenario, we have a triangle with one known interior angle of 35°, an unknown interior angle y, and an unknown exterior angle x. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Here, the equation is set up as x = 35° + y. Furthermore, the angles 3x and x are supplementary, allowing you to solve for x. Having solved for x, you can then solve for y. |
Applications of Triangles |

|
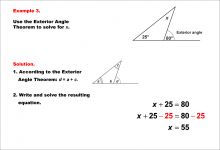
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 2 | Equations Using the Exterior Angle Theorem--Example 2TopicEquations |
Applications of Triangles |
|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 3 | Equations Using the Exterior Angle Theorem--Example 3TopicEquations |
Applications of Triangles |
|
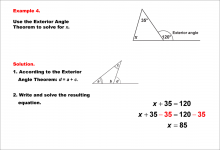
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 4 | Equations Using the Exterior Angle Theorem--Example 4TopicEquations |
Applications of Triangles |
|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 5 | Equations Using the Exterior Angle Theorem--Example 5TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 6 | Equations Using the Exterior Angle Theorem--Example 6TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 7 | Equations Using the Exterior Angle Theorem--Example 7TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 8 | Equations Using the Exterior Angle Theorem--Example 8TopicEquations |
Applications of Triangles |

|
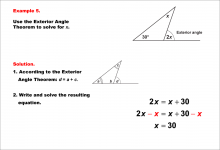
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 9 | Equations Using the Exterior Angle Theorem--Example 9TopicEquations DescriptionThis example presents a more challenging application of the Exterior Angle Theorem in solving triangle-related equations. In this scenario, we have a triangle with one known interior angle of 25°, an unknown interior angle y, and an unknown exterior angle x. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Here, the equation is set up as x = 25° + y. You can also use the fact that x and 2x are supplementary, allowing you to solve for x. By solving for x, you can then solve for y using the triangle equation. |
Applications of Triangles |
|
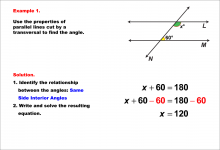
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 1 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 1TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
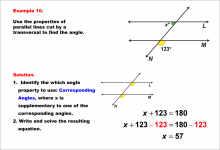
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 10 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 10TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
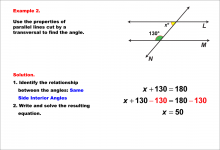
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 2 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 2TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
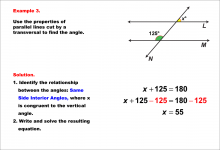
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 3 | TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
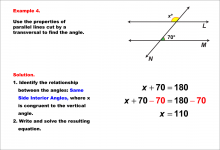
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 4 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 4TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
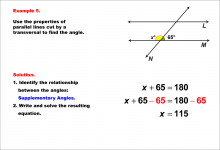
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 5 | TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
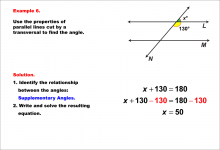
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 6 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 6TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
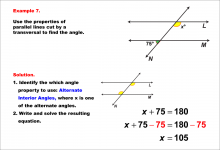
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 7 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 7TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
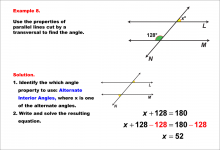
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 8 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 8TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
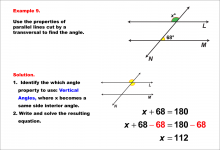
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 9 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 9TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |

|
Math Example--Solving Equations--Equations with Fractions: Example 1 | Equations with Fractions: Example 1TopicEquations |
Solving Fraction Equations |

|
Math Example--Solving Equations--Equations with Fractions: Example 10 | Equations with Fractions: Example 10TopicEquations DescriptionThis example illustrates solving Equations with Fractions: Example 10 which involves fractions. These equations can be addressed by first removing the fractions by finding a common denominator and multiplying through. This transforms the equation into a standard linear form that can then be solved by isolating the variable. The specific equation in the image shows the importance of maintaining accuracy in operations, and understanding the process is crucial for advancing in algebra. |
Solving Fraction Equations |