
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 10: Different Options for Solving One Equation
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Systems of Equations--Matrices--Example 4 | Math Example--Systems of Equations--Matrices--Example 4
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 5 | Math Example--Systems of Equations--Matrices--Example 5
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 6 | Math Example--Systems of Equations--Matrices--Example 6
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 7 | Math Example--Systems of Equations--Matrices--Example 7
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 8 | Math Example--Systems of Equations--Matrices--Example 8
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 1 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 1TopicSystems of Equations DescriptionThis image demonstrates solving the system y = 20x + 1 and y = 4x + 1 using elimination. The equations are manipulated by multiplying the second equation by -5 to align coefficients, yielding -5y = -20x - 5. Adding the equations eliminates x, resulting in -4y = -4 or y = 1. Substituting y = 1 into y = 20x + 1 solves x = 0. The intersection point is (0, 1). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 10 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 10TopicSystems of Equations DescriptionThe system y = x + 4 and y = 2x - 5 is solved using elimination. Multiplying the first equation by -2 gives -2y = -2x - 8. Adding cancels x, resulting in -y = -13 or y = 13. Substituting y = 13 into y = x + 4 finds x = 9. The solution is (9, 13). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 2 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 2TopicSystems of Equations DescriptionThis example explains solving y = -12x + 7 and y = -6x + 1 through elimination. The second equation is multiplied by -2, giving -2y = 12x - 2. Adding eliminates x, producing -y = 5 or y = -5. Substituting y = -5 into y = -12x + 7 solves x = 1. The solution is (1, -5). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 3 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 3TopicSystems of Equations DescriptionThis image solves y = 8x - 1 and y = -2x - 1 using elimination. Multiplying the second equation by 4 gives 4y = -8x - 4. Adding eliminates x, leaving 5y = -5 or y = -1. Substituting y = -1 into y = 8x - 1 solves x = 0. The intersection is (0, -1). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 4 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 4TopicSystems of Equations DescriptionThe system y = 2x - 9 and y = -x + 3 is solved via elimination. Doubling the second equation yields 2y = -2x + 6. Adding removes x, leaving 3y = -3 or y = -1. Substituting y = -1 into y = 2x - 9 solves x = 4. The solution is (4, -1). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 5 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 5TopicSystems of Equations DescriptionThis example solves y = 9x + 2 and y = 3x + 2 through elimination. The second equation is multiplied by -3, giving -3y = -9x - 6. Adding eliminates x, yielding -2y = -4 or y = 2. Substituting y = 2 into y = 9x + 2 finds x = 0. The solution is (0, 2). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 6 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 6TopicSystems of Equations DescriptionThis example uses elimination for y = -x - 5 and y = 5x + 7. Multiplying the first equation by 5 produces 5y = -5x - 25. Adding eliminates x, resulting in 6y = -18 or y = -3. Substituting y = -3 into y = -x - 5 finds x = -2. The intersection is (-2, -3). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 7 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 7TopicSystems of Equations DescriptionThis image explains solving y = -x + 9 and y = -2x + 2. Multiplying the first equation by -2 gives -2y = 2x - 18. Adding cancels x, leaving -y = -16 or y = 16. Substituting y = 16 into y = -x + 9 solves x = -7. The intersection is (-7, 16). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 8 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 8TopicSystems of Equations DescriptionThe system y = -6x + 4 and y = -12x - 8 is solved via elimination. Doubling the first equation gives -2y = 12x - 8. Adding eliminates x, resulting in -y = -16 or y = 16. Substituting y = 16 into y = -6x + 4 finds x = -2. The solution is (-2, 16). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 9 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 9TopicSystems of Equations DescriptionThis example solves y = x - 4 and y = 3x + 10 through elimination. Multiplying the first equation by -3 gives -3y = -3x + 12. Adding eliminates x, yielding -2y = 22 or y = -11. Substituting y = -11 into y = x - 4 solves x = -7. The intersection point is (-7, -11). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
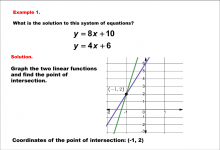
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 1 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 1TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This image solves y = 8x + 10 and y = 4x + 6 graphically. The two linear equations are plotted, and their intersection is visually identified as (-1, 2). The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
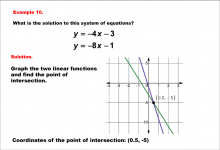
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 10 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 10TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This example graphically solves y = -4x - 3 and y = -8x - 1. The lines intersect at (0.5, -5), which is marked on the graph. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
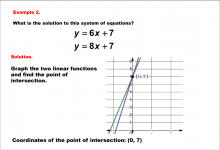
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 2 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 2TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This image demonstrates solving y = 6x + 7 and y = 8x + 7 by graphing. The point of intersection, clearly marked on the graph, is (0, 7). Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
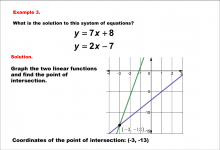
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 3 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 3TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This example illustrates solving y = 7x + 8 and y = 2x - 7 graphically. The intersection point is identified as (-3, -13) by observing where the lines cross. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
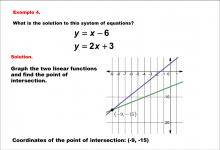
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 4 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 4TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: Graphing y = x - 6 and y = 2x + 3 shows their intersection point at (-9, -15). The graph displays both linear equations and highlights the solution. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
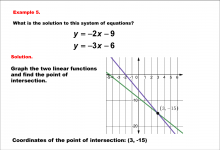
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 5 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 5TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This image uses graphing to solve y = -2x - 9 and y = -3x - 6. The intersection point is identified as (3, -15). Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
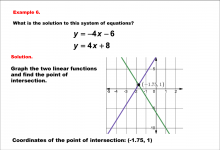
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 6 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 6TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: The system y = -4x - 6 and y = 4x + 8 is solved graphically. The lines intersect at (-1.75, 1), as indicated on the graph. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
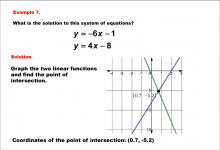
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 7 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 7TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This example solves y = -6x - 1 and y = 4x - 8 graphically. The intersection point, marked on the graph, is approximately (0.7, -5.2). Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
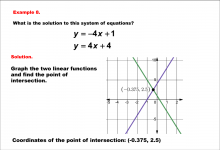
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 8 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 8TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: The equations y = -4x + 1 and y = 4x + 4 are graphed to find the intersection at (-0.375, 2.5). The graph highlights where the two lines meet. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
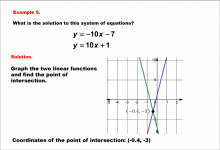
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 9 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 9TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: Graphing y = -10x - 7 and y = 10x + 1 reveals their intersection point at (-0.4, -3). The graph displays this visually with the crossing of the two lines. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 1 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 1TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: a system of linear equations using substitution. The equations y = -6x + 1 and y = 5x + 1 are solved to find their intersection point. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 10 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 10TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This example solves y = 7x - 10 and y = 5x - 5. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 2 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 2TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: the system of equations y = -x + 3 and y = -3x + 5. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 3 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 3TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: y = 2x + 6 and y = 3x - 2 using substitution. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 4 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 4TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: the equations y = 2x + 9 and y = -3x - 1. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 5 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 5TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: y = -3x + 4 and y = -9x - 8. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 6 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 6TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This example solves y = -9x + 5 and y = -8x + 6. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 7 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 7TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This image solves y = -3x - 9 and y = -2x - 4. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 8 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 8TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This example calculates the intersection of y = -5x - 9 and y = -6x + 6. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 9 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 9TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: y = -7x + 2 and y = -6x - 10 are solved. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 1 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 1
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 10 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 10
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 11 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 11
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 12 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 12
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 2 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 2
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 3 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 3
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 4 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 4
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 5 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 5
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 6 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 6
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 7 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 7
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 8 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 8
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations Using the Properties of Equality--Example 9 | Math Example: Solving One-Step Equations Using the Properties of Equality--Example 9
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations: Example 1 | Math Example: Solving One-Step Equations: Example 1
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations: Example 10 | Math Example: Solving One-Step Equations: Example 10
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |

|
Math Example: Solving One-Step Equations: Example 11 | Math Example: Solving One-Step Equations: Example 11
This is part of a collection of math examples that show how to solve one-step equations that include addition, subtraction, multiplication, or division. |
Solving One-Step Equations |