
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 12: Solving Problems about Percent Increase or Decrease
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
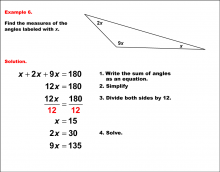
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 6 | Solving Equations with Angle Measures--Example 6TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 7 | Solving Equations with Angle Measures--Example 7TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 8 | Solving Equations with Angle Measures--Example 8TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 9 | Solving Equations with Angle Measures--Example 9TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
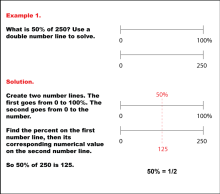
Math Example: Percents with Double Number Lines: Example 1 | Math Example: Percents with Double Number Lines: Example 1TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 50% of 250 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 250. By aligning 50% on the percentage line with its corresponding value on the numerical line, we can see that 50% of 250 is 125. This method visually represents the concept that 50% is equivalent to one-half of a quantity. |
Ratios and Rates |
|
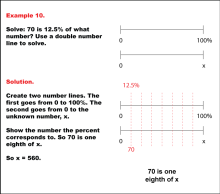
Math Example: Percents with Double Number Lines: Example 10 | Math Example: Percents with Double Number Lines: Example 10TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine an unknown value using a double number line when given a part and its corresponding percentage, involving a decimal percentage. The image shows two number lines: one ranging from 0 to 100% and another from 0 to an unknown number x. The position 70 is marked on the second line, visually illustrating the process of finding x when 70 is 12.5% of x. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 11 | Math Example: Percents with Double Number Lines: Example 11TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 75, with 25 marked as an intermediate point. This visual representation helps students understand the relationship between the part (25) and the whole (75) in percentage terms. |
Ratios and Rates |
|
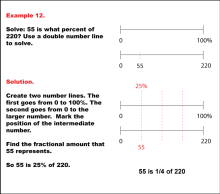
Math Example: Percents with Double Number Lines: Example 12 | Math Example: Percents with Double Number Lines: Example 12TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 220, with 55 marked as an intermediate point. This visual representation helps students understand the relationship between the part (55) and the whole (220) in percentage terms. |
Ratios and Rates |
|
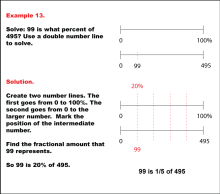
Math Example: Percents with Double Number Lines: Example 13 | Math Example: Percents with Double Number Lines: Example 13TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 495, with 99 marked as an intermediate point. This visual representation helps students understand the relationship between the part (99) and the whole (495) in percentage terms. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 14 | Math Example: Percents with Double Number Lines: Example 14TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 396, with 198 marked at the midpoint. This visual representation helps students understand the relationship between the part (198) and the whole (396) in percentage terms. |
Ratios and Rates |
|
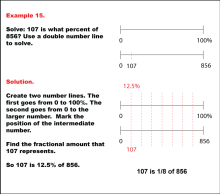
Math Example: Percents with Double Number Lines: Example 15 | Math Example: Percents with Double Number Lines: Example 15TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line, particularly when dealing with more complex ratios. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 856, with 107 marked at an eighth of the way. This visual representation helps students understand the relationship between the part (107) and the whole (856) in percentage terms. |
Ratios and Rates |
|
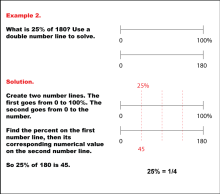
Math Example: Percents with Double Number Lines: Example 2 | Math Example: Percents with Double Number Lines: Example 2TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate 25% of 180 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 180. By aligning 25% on the percentage line with its corresponding value on the numerical line, we can determine that 25% of 180 is 45. This method visually demonstrates that 25% is equivalent to one-quarter of a quantity. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 3 | Math Example: Percents with Double Number Lines: Example 3TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 33 1/3% of 240 using a double number line. The solution displays two parallel number lines: one ranging from 0 to 100% and the other from 0 to 240. By aligning 33 1/3% on the percentage line with its corresponding value on the numerical line, we can see that 33 1/3% of 240 is 80. This method visually represents the concept that 33 1/3% is equivalent to one-third of a quantity. |
Ratios and Rates |
|
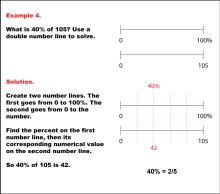
Math Example: Percents with Double Number Lines: Example 4 | Math Example: Percents with Double Number Lines: Example 4TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate 40% of 105 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 105. By aligning 40% on the percentage line with its corresponding value on the numerical line, we can determine that 40% of 105 is 42. This method visually demonstrates that 40% is equivalent to two-fifths of a quantity. |
Ratios and Rates |
|
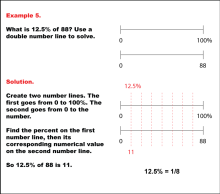
Math Example: Percents with Double Number Lines: Example 5 | Math Example: Percents with Double Number Lines: Example 5TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 12.5% of 88 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 88. By aligning 12.5% on the percentage line with its corresponding value on the numerical line, we can see that 12.5% of 88 is 11. This method visually represents the concept that 12.5% is equivalent to one-eighth of a quantity. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 6 | Math Example: Percents with Double Number Lines: Example 6TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to solve for an unknown value using a double number line when given a percentage. The image features two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 75 is 50% of x. |
Ratios and Rates |
|
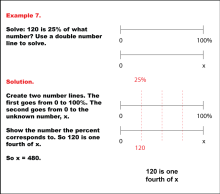
Math Example: Percents with Double Number Lines: Example 7 | Math Example: Percents with Double Number Lines: Example 7TopicRatios, Proportions, Percents DescriptionThis example illustrates how to determine an unknown value using a double number line when given a part and its corresponding percentage. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to an unknown value x. It visually demonstrates the process of finding x when 120 is 25% of x. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 8 | Math Example: Percents with Double Number Lines: Example 8TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find an unknown value using a double number line when given a part and its corresponding percentage, involving a fractional percentage. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 125 is 33 1/3% of x. |
Ratios and Rates |
|
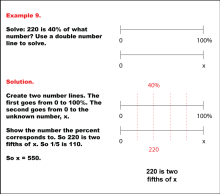
Math Example: Percents with Double Number Lines: Example 9 | Math Example: Percents with Double Number Lines: Example 9TopicRatios, Proportions, Percents DescriptionThis example illustrates how to solve for an unknown value using a double number line when given a part and its corresponding percentage. The image shows two horizontal number lines: the top line ranges from 0 to 100%, and the bottom line ranges from 0 to an unknown number x. The 40% mark on the top line aligns with 220 on the bottom line, visually demonstrating the process of finding x when 220 is 40% of x. |
Ratios and Rates |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition demonstrates solving the equation 2x + 3 = 7 by performing two inverse operations to isolate x. The operations shown are subtracting 3 from both sides and then dividing by 2. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 10 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 10TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition involves solving -3x + (-12) = -42 by performing two inverse operations: addition and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 2 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 2TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows solving the equation 3x + 4 = 13 by using two inverse operations. The steps involve subtracting 4 and then dividing by 3. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 3 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 3TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition involves solving the equation 2x + 4 = 8 using inverse operations. It shows subtraction and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 4 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 4TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition illustrates solving -4x + 5 = 25. It uses inverse operations by subtracting 5 and dividing by -4. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 5 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 5TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows the solution to -7x + 6 = 48 by isolating x with inverse operations, including subtraction and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 6 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 6TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition solves the equation 6x + (-2) = 34 by using inverse operations, specifically addition and division, to find the value of x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 7 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 7TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition solves 10x + (-6) = 54 by isolating x through inverse operations, including addition and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 8 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 8TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows solving -x + (-5) = 71 by performing inverse operations to isolate x, using addition and division by -1. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 9 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 9TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition demonstrates solving -2x + (-8) = 22 through inverse operations, specifically addition and division, to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction shows solving the equation 2x - 3 = 7 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 10 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 10TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation -3x - (-12) = -42 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 2 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 2TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction illustrates solving the equation 3x - 4 = 14 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 3 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 3TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation -2x - 4 = 8 by isolating x using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 4 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 4TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction explains solving the equation -x - 5 = 17 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 5 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 5TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction shows solving the equation -7x - 6 = 43 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 6 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 6TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction illustrates solving the equation 6x - (-2) = 38 by isolating x using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 7 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 7TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation 10x - (-6) = 76 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 8 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 8TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction explains solving the equation -x - (-5) = 71 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 9 | Math Example: Solving Two-Step Equations of the Form ax - b = c--Example 9TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and subtraction shows solving the equation -2x - (-8) = 22 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: x/5 + 3 = 7. The solution is detailed with inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 10 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 10TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: -x/3 + (-12) = -42. The solution follows each step using inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 2 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 2TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: x/4 + 4 = 14. It includes each step to isolate the variable using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 3 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 3TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: -x/3 + 4 = 8. The solution uses inverse operations to isolate x with careful handling of the negative sign. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 4 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 4TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: -x/6 + 5 = 17. The solution details each inverse operation step to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 5 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 5TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: -x/7 + 6 = 43. The solution carefully applies inverse operations to solve for x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 6 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 6TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: x/6 + (-2) = 38, showing each step to isolate x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 7 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 7TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: x/10 + (-6) = 76. Each inverse operation is shown to solve for x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 8 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 8TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: -x/9 + (-5) = 71. The solution includes each inverse operation needed to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 9 | Math Example: Solving Two-Step Equations of the Form x/a + b = c--Example 9TopicSolving Equations DescriptionAn example of solving a two-step equation with division and addition: -x/2 + (-8) = 22, detailing the inverse operations step-by-step to solve for x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form x/a - b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form x/a - b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation with division and subtraction: x / 5 - 3 = 7 using two inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |