
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 12: Solving Problems about Percent Increase or Decrease
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 8 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 8TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving for d in a proportion where a = 11, b = 5, and c is expressed as x - 4. We set up the equation 11 / 5 = (x - 4) / d and solve for d, resulting in the expression d = (5(x - 4)) / 11. This problem demonstrates how to handle algebraic expressions in the numerator of a proportion. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 9 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 9TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar triangles. Two triangles are shown, with one having sides of 3 and 4, and the other having sides of 6 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 3 / 4 = 6 / x. Solving this equation leads to x = 8. |
Proportions |

|
Math Example--Solving Equations--One-Variable Equations: Example 1 | One-Variable Equations: Example 1TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 10 | One-Variable Equations: Example 10TopicEquations DescriptionThis example involves solving a one-variable equation that may include complex terms or require multiple steps to simplify. The equation might involve fractions, decimals, or variables on both sides. Solving it involves using inverse operations, distributing terms, and combining like terms to isolate the variable. This type of problem helps students refine their algebraic skills and understand the importance of systematic problem-solving. Checking the solution by substituting it back into the original equation is a crucial step to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 11 | One-Variable Equations: Example 11TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 12 | One-Variable Equations: Example 12TopicEquations DescriptionThis example presents a one-variable equation that may involve variables on both sides. The solving process requires moving all terms involving the variable to one side and constants to the other. This often involves using the distributive property and combining like terms. The goal is to isolate the variable and solve for its value. This type of problem helps students develop their algebraic manipulation skills and understand the importance of maintaining balance in an equation. Checking the solution by substituting it back into the original equation is crucial to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 13 | One-Variable Equations: Example 13TopicEquations DescriptionThis example involves solving a one-variable equation that might include complex expressions, such as those with parentheses or multiple terms. The solving process may require using the distributive property to eliminate parentheses and combining like terms to simplify the equation. After simplification, standard techniques are used to isolate the variable. This example reinforces the importance of following the order of operations and checking the solution for accuracy. Mastery of these skills is essential for tackling more advanced algebraic problems. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 14 | One-Variable Equations: Example 14TopicEquations DescriptionThis example deals with solving a one-variable equation that may involve more complex algebraic expressions, such as nested parentheses or fractional coefficients. The solving process requires careful application of the distributive property and combining like terms. After simplifying the equation, inverse operations are used to isolate the variable. This example highlights the importance of precision in algebraic manipulation and the necessity of verifying solutions by substituting them back into the original equation to ensure correctness. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 15 | One-Variable Equations: Example 15TopicEquations DescriptionThis example involves solving a one-variable equation that may include complex terms or require multiple steps to simplify. The equation might involve fractions, decimals, or variables on both sides. Solving it involves using inverse operations, distributing terms, and combining like terms to isolate the variable. This type of problem helps students refine their algebraic skills and understand the importance of systematic problem-solving. Checking the solution by substituting it back into the original equation is a crucial step to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 16 | One-Variable Equations: Example 16TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 17 | One-Variable Equations: Example 17TopicEquations DescriptionThis example presents a one-variable equation that may involve variables on both sides. The solving process requires moving all terms involving the variable to one side and constants to the other. This often involves using the distributive property and combining like terms. The goal is to isolate the variable and solve for its value. This type of problem helps students develop their algebraic manipulation skills and understand the importance of maintaining balance in an equation. Checking the solution by substituting it back into the original equation is crucial to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 18 | One-Variable Equations: Example 18TopicEquations DescriptionThis example involves solving a one-variable equation that might include complex expressions, such as those with parentheses or multiple terms. The solving process may require using the distributive property to eliminate parentheses and combining like terms to simplify the equation. After simplification, standard techniques are used to isolate the variable. This example reinforces the importance of following the order of operations and checking the solution for accuracy. Mastery of these skills is essential for tackling more advanced algebraic problems. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 19 | One-Variable Equations: Example 19TopicEquations DescriptionThis example deals with solving a one-variable equation that may involve more complex algebraic expressions, such as nested parentheses or fractional coefficients. The solving process requires careful application of the distributive property and combining like terms. After simplifying the equation, inverse operations are used to isolate the variable. This example highlights the importance of precision in algebraic manipulation and the necessity of verifying solutions by substituting them back into the original equation to ensure correctness. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 2 | One-Variable Equations: Example 2TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 20 | One-Variable Equations: Example 20TopicEquations DescriptionThis example involves solving a one-variable equation that may include complex terms or require multiple steps to simplify. The equation might involve fractions, decimals, or variables on both sides. Solving it involves using inverse operations, distributing terms, and combining like terms to isolate the variable. This type of problem helps students refine their algebraic skills and understand the importance of systematic problem-solving. Checking the solution by substituting it back into the original equation is a crucial step to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 21 | One-Variable Equations: Example 21TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 22 | One-Variable Equations: Example 22TopicEquations DescriptionThis example presents a one-variable equation that may involve variables on both sides. The solving process requires moving all terms involving the variable to one side and constants to the other. This often involves using the distributive property and combining like terms. The goal is to isolate the variable and solve for its value. This type of problem helps students develop their algebraic manipulation skills and understand the importance of maintaining balance in an equation. Checking the solution by substituting it back into the original equation is crucial to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 23 | One-Variable Equations: Example 23TopicEquations DescriptionThis example involves solving a one-variable equation that might include complex expressions, such as those with parentheses or multiple terms. The solving process may require using the distributive property to eliminate parentheses and combining like terms to simplify the equation. After simplification, standard techniques are used to isolate the variable. This example reinforces the importance of following the order of operations and checking the solution for accuracy. Mastery of these skills is essential for tackling more advanced algebraic problems. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 24 | One-Variable Equations: Example 24TopicEquations DescriptionThis example deals with solving a one-variable equation that may involve more complex algebraic expressions, such as nested parentheses or fractional coefficients. The solving process requires careful application of the distributive property and combining like terms. After simplifying the equation, inverse operations are used to isolate the variable. This example highlights the importance of precision in algebraic manipulation and the necessity of verifying solutions by substituting them back into the original equation to ensure correctness. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 25 | One-Variable Equations: Example 25TopicEquations DescriptionThis example involves solving a one-variable equation that may include complex terms or require multiple steps to simplify. The equation might involve fractions, decimals, or variables on both sides. Solving it involves using inverse operations, distributing terms, and combining like terms to isolate the variable. This type of problem helps students refine their algebraic skills and understand the importance of systematic problem-solving. Checking the solution by substituting it back into the original equation is a crucial step to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 26 | One-Variable Equations: Example 26TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 27 | One-Variable Equations: Example 27TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 3 | One-Variable Equations: Example 3TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 4 | One-Variable Equations: Example 4TopicEquations DescriptionThis example likely demonstrates solving a more complex one-variable equation. It may involve multiple steps, such as combining like terms, using the distributive property, or dealing with fractions or decimals. The solving process typically includes isolating the variable on one side of the equation by performing inverse operations on both sides. This type of problem enhances students' algebraic manipulation skills and prepares them for more advanced equation solving. The specific solution would involve carefully following the order of operations and checking the final answer by substituting it back into the original equation. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 5 | One-Variable Equations: Example 5TopicEquations DescriptionThis example likely showcases a more challenging one-variable equation. It may involve variables on both sides of the equation, requiring students to consolidate like terms before solving. The problem might also include parentheses, necessitating the use of the distributive property. Solving this equation would involve carefully balancing operations on both sides, possibly dealing with negative numbers or fractions. This type of problem helps students develop their algebraic reasoning skills and reinforces the importance of maintaining equation balance throughout the solving process. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 6 | One-Variable Equations: Example 6TopicEquations |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 7 | One-Variable Equations: Example 7TopicEquations DescriptionThis example presents a one-variable equation that may involve variables on both sides. The solving process requires moving all terms involving the variable to one side and constants to the other. This often involves using the distributive property and combining like terms. The goal is to isolate the variable and solve for its value. This type of problem helps students develop their algebraic manipulation skills and understand the importance of maintaining balance in an equation. Checking the solution by substituting it back into the original equation is crucial to ensure accuracy. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 8 | One-Variable Equations: Example 8TopicEquations DescriptionThis example involves solving a one-variable equation that might include complex expressions, such as those with parentheses or multiple terms. The solving process may require using the distributive property to eliminate parentheses and combining like terms to simplify the equation. After simplification, standard techniques are used to isolate the variable. This example reinforces the importance of following the order of operations and checking the solution for accuracy. Mastery of these skills is essential for tackling more advanced algebraic problems. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |

|
Math Example--Solving Equations--One-Variable Equations: Example 9 | One-Variable Equations: Example 9TopicEquations DescriptionThis example deals with solving a one-variable equation that may involve more complex algebraic expressions, such as nested parentheses or fractional coefficients. The solving process requires careful application of the distributive property and combining like terms. After simplifying the equation, inverse operations are used to isolate the variable. This example highlights the importance of precision in algebraic manipulation and the necessity of verifying solutions by substituting them back into the original equation to ensure correctness. |
Solving Multistep Equations, Solving One-Step Equations and Solving Two-Step Equations |
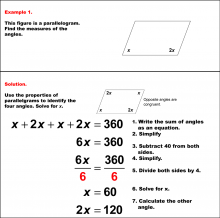
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 1 | Solving Equations with Angle Measures 2--Example 1TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 10 | Solving Equations with Angle Measures 2--Example 10TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
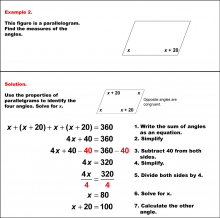
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 2 | Solving Equations with Angle Measures 2--Example 2TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
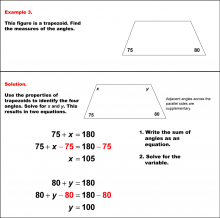
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 3 | Solving Equations with Angle Measures 2--Example 3TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
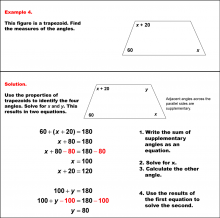
|
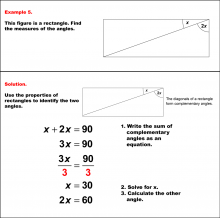
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 4 | Solving Equations with Angle Measures 2--Example 4TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 5 | Solving Equations with Angle Measures 2--Example 5TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
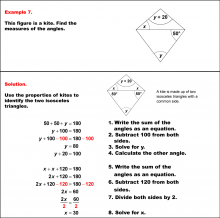
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 6 | Solving Equations with Angle Measures 2--Example 6TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
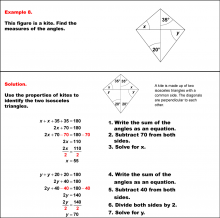
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 7 | Solving Equations with Angle Measures 2--Example 7TopicEquations DescriptionThis example demonstrates solving equations involving angle measures in a kite. A kite has two pairs of adjacent congruent angles. In this case, we have angles represented as (x+50)°, (x+50)°, (y+20)°, and y°. To solve this problem, we apply two key principles: the sum of angles in a quadrilateral is 360°, and the sum of the angles of a triangle is 180°. You can use the triangle equation to solve for y. Once you determine the value for y, you can use that to find x using either the triangle or the quadrilateral equation. In the solution shown, the triangle equation is used. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
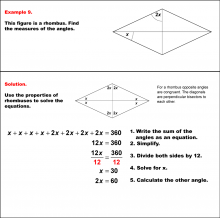
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 8 | Solving Equations with Angle Measures 2--Example 8TopicEquations DescriptionThis example illustrates solving equations involving angle measures in a kite. The kite has two known angles of 70° and 40°, and two unknown angles represented as (x+y)°. To solve this problem, we look at the triangles formed by one of the diagonals of the kite and use the triangle equation. First solve for x with the top triangle. Once you find x, use that value to solve for y in the bottom triangle. You could also use the quadrilateral equation to solve for y. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 9 | Solving Equations with Angle Measures 2--Example 9TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 1 | Solving Equations with Angle Measures--Example 1TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 10 | Solving Equations with Angle Measures--Example 10TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 11 | Solving Equations with Angle Measures--Example 11TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 12 | Solving Equations with Angle Measures--Example 12TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 13 | Solving Equations with Angle Measures--Example 13TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 14 | Solving Equations with Angle Measures--Example 14TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
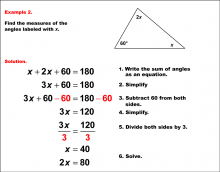
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 15 | Solving Equations with Angle Measures--Example 15TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 2 | Solving Equations with Angle Measures--Example 2TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 3 | Solving Equations with Angle Measures--Example 3TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 4 | Solving Equations with Angle Measures--Example 4TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 5 | Solving Equations with Angle Measures--Example 5TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |