Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
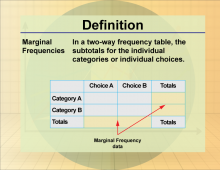
Definition--Statistics and Probability Concepts--Marginal Frequencies	Marginal Frequencies Topic Statistics and Probability Definition Marginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. Description Marginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population.	Data Analysis
Definition--Statistics and Probability Concepts--Marginal Frequencies	Marginal Frequencies Topic Statistics and Probability Definition Marginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. Description Marginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population.	Data Analysis
Definition--Statistics and Probability Concepts--Marginal Frequencies	Marginal Frequencies Topic Statistics and Probability Definition Marginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. Description Marginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population.	Data Analysis
Definition--Statistics and Probability Concepts--Marginal Frequencies	Marginal Frequencies Topic Statistics and Probability Definition Marginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. Description Marginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population.	Data Analysis
Definition--Statistics and Probability Concepts--Marginal Frequencies	Marginal Frequencies Topic Statistics and Probability Definition Marginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. Description Marginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population.	Data Analysis
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability	Multiplication Rule of Probability Topic Statistics and Probability Definition The multiplication rule of probability is used to find the probability of two independent events both occurring. Description The multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory.	Data Analysis
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability	Multiplication Rule of Probability Topic Statistics and Probability Definition The multiplication rule of probability is used to find the probability of two independent events both occurring. Description The multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory.	Data Analysis
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability	Multiplication Rule of Probability Topic Statistics and Probability Definition The multiplication rule of probability is used to find the probability of two independent events both occurring. Description The multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory.	Data Analysis
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability	Multiplication Rule of Probability Topic Statistics and Probability Definition The multiplication rule of probability is used to find the probability of two independent events both occurring. Description The multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory.	Data Analysis
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability	Multiplication Rule of Probability Topic Statistics and Probability Definition The multiplication rule of probability is used to find the probability of two independent events both occurring. Description The multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory.	Data Analysis
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability	Multiplication Rule of Probability Topic Statistics and Probability Definition The multiplication rule of probability is used to find the probability of two independent events both occurring. Description The multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory.	Data Analysis
Definition--Statistics and Probability Concepts--Permutation 1	Permutation 1 Topic Statistics and Probability Definition A permutation is an arrangement of items in a specific order. Description Permutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is	Data Analysis
Definition--Statistics and Probability Concepts--Permutation 1	Permutation 1 Topic Statistics and Probability Definition A permutation is an arrangement of items in a specific order. Description Permutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is	Data Analysis
Definition--Statistics and Probability Concepts--Permutation 1	Permutation 1 Topic Statistics and Probability Definition A permutation is an arrangement of items in a specific order. Description Permutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is	Data Analysis
Definition--Statistics and Probability Concepts--Permutation 1	Permutation 1 Topic Statistics and Probability Definition A permutation is an arrangement of items in a specific order. Description Permutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is	Data Analysis
Definition--Statistics and Probability Concepts--Permutation 1	Permutation 1 Topic Statistics and Probability Definition A permutation is an arrangement of items in a specific order. Description Permutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is	Data Analysis
Definition--Statistics and Probability Concepts--Permutation 1	Permutation 1 Topic Statistics and Probability Definition A permutation is an arrangement of items in a specific order. Description Permutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is	Data Analysis
Definition--Statistics and Probability Concepts--Population	Population Topic Statistics and Probability Definition A population is the entire group under consideration in a statistical study. Description Population is a fundamental concept in statistics, representing the complete set of individuals or items that share a common characteristic. Understanding a population is crucial for statistical analysis as it serves as the basis for sampling and inferential statistics.	Data Gathering
Definition--Statistics and Probability Concepts--Population	Population Topic Statistics and Probability Definition A population is the entire group under consideration in a statistical study. Description Population is a fundamental concept in statistics, representing the complete set of individuals or items that share a common characteristic. Understanding a population is crucial for statistical analysis as it serves as the basis for sampling and inferential statistics.	Data Gathering
Definition--Statistics and Probability Concepts--Population	Population Topic Statistics and Probability Definition A population is the entire group under consideration in a statistical study. Description Population is a fundamental concept in statistics, representing the complete set of individuals or items that share a common characteristic. Understanding a population is crucial for statistical analysis as it serves as the basis for sampling and inferential statistics.	Data Gathering
Definition--Statistics and Probability Concepts--Population	Population Topic Statistics and Probability Definition A population is the entire group under consideration in a statistical study. Description Population is a fundamental concept in statistics, representing the complete set of individuals or items that share a common characteristic. Understanding a population is crucial for statistical analysis as it serves as the basis for sampling and inferential statistics.	Data Gathering
Definition--Statistics and Probability Concepts--Population	Population Topic Statistics and Probability Definition A population is the entire group under consideration in a statistical study. Description Population is a fundamental concept in statistics, representing the complete set of individuals or items that share a common characteristic. Understanding a population is crucial for statistical analysis as it serves as the basis for sampling and inferential statistics.	Data Gathering
Definition--Statistics and Probability Concepts--Population	Population Topic Statistics and Probability Definition A population is the entire group under consideration in a statistical study. Description Population is a fundamental concept in statistics, representing the complete set of individuals or items that share a common characteristic. Understanding a population is crucial for statistical analysis as it serves as the basis for sampling and inferential statistics.	Data Gathering
Definition--Statistics and Probability Concepts--Probability Notation	Probability Notation Topic Statistics and Probability Definition Probability notation is a standardized way of expressing probabilities. Description Probability notation provides a concise language for defining and communicating probabilities in mathematics. It helps in avoiding confusion in statistical communication. Common symbols include P(A) for the probability of event A occurring.	Data Analysis
Definition--Statistics and Probability Concepts--Probability Notation	Probability Notation Topic Statistics and Probability Definition Probability notation is a standardized way of expressing probabilities. Description Probability notation provides a concise language for defining and communicating probabilities in mathematics. It helps in avoiding confusion in statistical communication. Common symbols include P(A) for the probability of event A occurring.	Data Analysis
Definition--Statistics and Probability Concepts--Probability Notation	Probability Notation Topic Statistics and Probability Definition Probability notation is a standardized way of expressing probabilities. Description Probability notation provides a concise language for defining and communicating probabilities in mathematics. It helps in avoiding confusion in statistical communication. Common symbols include P(A) for the probability of event A occurring.	Data Analysis
Definition--Statistics and Probability Concepts--Probability Notation	Probability Notation Topic Statistics and Probability Definition Probability notation is a standardized way of expressing probabilities. Description Probability notation provides a concise language for defining and communicating probabilities in mathematics. It helps in avoiding confusion in statistical communication. Common symbols include P(A) for the probability of event A occurring.	Data Analysis
Definition--Statistics and Probability Concepts--Probability Notation	Probability Notation Topic Statistics and Probability Definition Probability notation is a standardized way of expressing probabilities. Description Probability notation provides a concise language for defining and communicating probabilities in mathematics. It helps in avoiding confusion in statistical communication. Common symbols include P(A) for the probability of event A occurring.	Data Analysis
Definition--Statistics and Probability Concepts--Probability Notation	Probability Notation Topic Statistics and Probability Definition Probability notation is a standardized way of expressing probabilities. Description Probability notation provides a concise language for defining and communicating probabilities in mathematics. It helps in avoiding confusion in statistical communication. Common symbols include P(A) for the probability of event A occurring.	Data Analysis
Definition--Statistics and Probability Concepts--Relative Frequency Table	Relative Frequency Table Topic Statistics and Probability Definition A relative frequency table displays the proportion of total occurrences for each category of data. Description Relative frequency tables are important in statistics as they summarize data in a way that makes it easy to analyze proportions and patterns within datasets. These tables allow for quick comparisons of different categories based on their frequency relative to the total.	Data Analysis
Definition--Statistics and Probability Concepts--Relative Frequency Table	Relative Frequency Table Topic Statistics and Probability Definition A relative frequency table displays the proportion of total occurrences for each category of data. Description Relative frequency tables are important in statistics as they summarize data in a way that makes it easy to analyze proportions and patterns within datasets. These tables allow for quick comparisons of different categories based on their frequency relative to the total.	Data Analysis
Definition--Statistics and Probability Concepts--Relative Frequency Table	Relative Frequency Table Topic Statistics and Probability Definition A relative frequency table displays the proportion of total occurrences for each category of data. Description Relative frequency tables are important in statistics as they summarize data in a way that makes it easy to analyze proportions and patterns within datasets. These tables allow for quick comparisons of different categories based on their frequency relative to the total.	Data Analysis
Definition--Statistics and Probability Concepts--Relative Frequency Table	Relative Frequency Table Topic Statistics and Probability Definition A relative frequency table displays the proportion of total occurrences for each category of data. Description Relative frequency tables are important in statistics as they summarize data in a way that makes it easy to analyze proportions and patterns within datasets. These tables allow for quick comparisons of different categories based on their frequency relative to the total.	Data Analysis
Definition--Statistics and Probability Concepts--Relative Frequency Table	Relative Frequency Table Topic Statistics and Probability Definition A relative frequency table displays the proportion of total occurrences for each category of data. Description Relative frequency tables are important in statistics as they summarize data in a way that makes it easy to analyze proportions and patterns within datasets. These tables allow for quick comparisons of different categories based on their frequency relative to the total.	Data Analysis
Definition--Statistics and Probability Concepts--Relative Frequency Table	Relative Frequency Table Topic Statistics and Probability Definition A relative frequency table displays the proportion of total occurrences for each category of data. Description Relative frequency tables are important in statistics as they summarize data in a way that makes it easy to analyze proportions and patterns within datasets. These tables allow for quick comparisons of different categories based on their frequency relative to the total.	Data Analysis
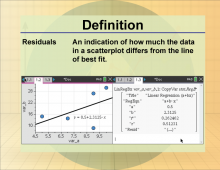
Definition--Statistics and Probability Concepts--Residuals	Residuals Topic Statistics and Probability Definition Residuals are the differences between observed and predicted values in a dataset. Description In statistics, residuals are crucial for assessing the accuracy of predictions generated by statistical models. They represent the errors in prediction, providing insight into the model's performance and areas for potential improvement.	Data Analysis
Definition--Statistics and Probability Concepts--Residuals	Residuals Topic Statistics and Probability Definition Residuals are the differences between observed and predicted values in a dataset. Description In statistics, residuals are crucial for assessing the accuracy of predictions generated by statistical models. They represent the errors in prediction, providing insight into the model's performance and areas for potential improvement.	Data Analysis
Definition--Statistics and Probability Concepts--Residuals	Residuals Topic Statistics and Probability Definition Residuals are the differences between observed and predicted values in a dataset. Description In statistics, residuals are crucial for assessing the accuracy of predictions generated by statistical models. They represent the errors in prediction, providing insight into the model's performance and areas for potential improvement.	Data Analysis
Definition--Statistics and Probability Concepts--Residuals	Residuals Topic Statistics and Probability Definition Residuals are the differences between observed and predicted values in a dataset. Description In statistics, residuals are crucial for assessing the accuracy of predictions generated by statistical models. They represent the errors in prediction, providing insight into the model's performance and areas for potential improvement.	Data Analysis
Definition--Statistics and Probability Concepts--Residuals	Residuals Topic Statistics and Probability Definition Residuals are the differences between observed and predicted values in a dataset. Description In statistics, residuals are crucial for assessing the accuracy of predictions generated by statistical models. They represent the errors in prediction, providing insight into the model's performance and areas for potential improvement.	Data Analysis
Definition--Statistics and Probability Concepts--Residuals	Residuals Topic Statistics and Probability Definition Residuals are the differences between observed and predicted values in a dataset. Description In statistics, residuals are crucial for assessing the accuracy of predictions generated by statistical models. They represent the errors in prediction, providing insight into the model's performance and areas for potential improvement.	Data Analysis
Definition--Statistics and Probability Concepts--Statistical Distribution	Statistical Distribution Topic Statistics and Probability Definition A statistical distribution describes how values of a variable are distributed. Description Statistical distributions are fundamental in understanding data behavior and variability. They are used in various fields, such as finance, to model asset returns, or in biology, to understand population dynamics. Common distributions include normal, binomial, and Poisson distributions, each with its own properties and applications.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Distribution	Statistical Distribution Topic Statistics and Probability Definition A statistical distribution describes how values of a variable are distributed. Description Statistical distributions are fundamental in understanding data behavior and variability. They are used in various fields, such as finance, to model asset returns, or in biology, to understand population dynamics. Common distributions include normal, binomial, and Poisson distributions, each with its own properties and applications.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Distribution	Statistical Distribution Topic Statistics and Probability Definition A statistical distribution describes how values of a variable are distributed. Description Statistical distributions are fundamental in understanding data behavior and variability. They are used in various fields, such as finance, to model asset returns, or in biology, to understand population dynamics. Common distributions include normal, binomial, and Poisson distributions, each with its own properties and applications.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Distribution	Statistical Distribution Topic Statistics and Probability Definition A statistical distribution describes how values of a variable are distributed. Description Statistical distributions are fundamental in understanding data behavior and variability. They are used in various fields, such as finance, to model asset returns, or in biology, to understand population dynamics. Common distributions include normal, binomial, and Poisson distributions, each with its own properties and applications.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Distribution	Statistical Distribution Topic Statistics and Probability Definition A statistical distribution describes how values of a variable are distributed. Description Statistical distributions are fundamental in understanding data behavior and variability. They are used in various fields, such as finance, to model asset returns, or in biology, to understand population dynamics. Common distributions include normal, binomial, and Poisson distributions, each with its own properties and applications.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Distribution	Statistical Distribution Topic Statistics and Probability Definition A statistical distribution describes how values of a variable are distributed. Description Statistical distributions are fundamental in understanding data behavior and variability. They are used in various fields, such as finance, to model asset returns, or in biology, to understand population dynamics. Common distributions include normal, binomial, and Poisson distributions, each with its own properties and applications.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Variability	Statistical Variability Topic Statistics and Probability Definition Statistical variability refers to the extent to which data points in a dataset differ from each other and from the central value. Description Understanding variability is essential in statistics as it provides insights into the consistency and reliability of data. Measures of variability, such as range, variance, and standard deviation, help in assessing the spread of data points around a central value.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Variability	Statistical Variability Topic Statistics and Probability Definition Statistical variability refers to the extent to which data points in a dataset differ from each other and from the central value. Description Understanding variability is essential in statistics as it provides insights into the consistency and reliability of data. Measures of variability, such as range, variance, and standard deviation, help in assessing the spread of data points around a central value.	Data Gathering
Definition--Statistics and Probability Concepts--Statistical Variability	Statistical Variability Topic Statistics and Probability Definition Statistical variability refers to the extent to which data points in a dataset differ from each other and from the central value. Description Understanding variability is essential in statistics as it provides insights into the consistency and reliability of data. Measures of variability, such as range, variance, and standard deviation, help in assessing the spread of data points around a central value.	Data Gathering

Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition