Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
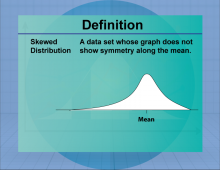
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Mean	Weighted Mean Topic Statistics Definition The weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. Description The weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Mean	Weighted Mean Topic Statistics Definition The weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. Description The weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis

Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition