Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
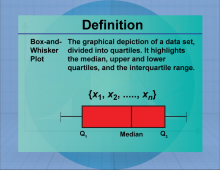
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis

Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition