Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
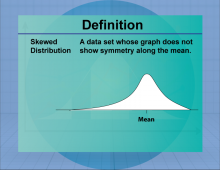
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis

Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 1: Mystery Bags

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition