
Illustrative Math Alignment: Grade 7 Unit 8
Probability and Sampling
Lesson 1: Mystery Bags
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Addition Rule of Probability | Addition Rule of ProbabilityTopicStatistics and Probability DefinitionThe Addition Rule of Probability is a key concept in statistics that helps in understanding the interaction between different events. DescriptionThe Addition Rule of Probability is crucial in the field of statistics because it allows us to make informed decisions based on the relationships between variables. For instance, in real-world applications, this concept is essential in various fields such as economics, social sciences, and health studies. Understanding how events affect each other can lead to better predictions and strategies. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Addition Rule of Probability | Addition Rule of ProbabilityTopicStatistics and Probability DefinitionThe Addition Rule of Probability is a key concept in statistics that helps in understanding the interaction between different events. DescriptionThe Addition Rule of Probability is crucial in the field of statistics because it allows us to make informed decisions based on the relationships between variables. For instance, in real-world applications, this concept is essential in various fields such as economics, social sciences, and health studies. Understanding how events affect each other can lead to better predictions and strategies. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Addition Rule of Probability | Addition Rule of ProbabilityTopicStatistics and Probability DefinitionThe Addition Rule of Probability is a key concept in statistics that helps in understanding the interaction between different events. DescriptionThe Addition Rule of Probability is crucial in the field of statistics because it allows us to make informed decisions based on the relationships between variables. For instance, in real-world applications, this concept is essential in various fields such as economics, social sciences, and health studies. Understanding how events affect each other can lead to better predictions and strategies. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Addition Rule of Probability | Addition Rule of ProbabilityTopicStatistics and Probability DefinitionThe Addition Rule of Probability is a key concept in statistics that helps in understanding the interaction between different events. DescriptionThe Addition Rule of Probability is crucial in the field of statistics because it allows us to make informed decisions based on the relationships between variables. For instance, in real-world applications, this concept is essential in various fields such as economics, social sciences, and health studies. Understanding how events affect each other can lead to better predictions and strategies. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Addition Rule of Probability | Addition Rule of ProbabilityTopicStatistics and Probability DefinitionThe Addition Rule of Probability is a key concept in statistics that helps in understanding the interaction between different events. DescriptionThe Addition Rule of Probability is crucial in the field of statistics because it allows us to make informed decisions based on the relationships between variables. For instance, in real-world applications, this concept is essential in various fields such as economics, social sciences, and health studies. Understanding how events affect each other can lead to better predictions and strategies. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Addition Rule of Probability | Addition Rule of ProbabilityTopicStatistics and Probability DefinitionThe Addition Rule of Probability is a key concept in statistics that helps in understanding the interaction between different events. DescriptionThe Addition Rule of Probability is crucial in the field of statistics because it allows us to make informed decisions based on the relationships between variables. For instance, in real-world applications, this concept is essential in various fields such as economics, social sciences, and health studies. Understanding how events affect each other can lead to better predictions and strategies. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Bivariate Data | Bivariate DataTopicStatistics and Probability DefinitionBivariate data involves the analysis of two variables to determine relationships between them. DescriptionBivariate data is essential in statistics as it allows for the exploration of relationships between two variables, such as height and weight. This analysis is used in various fields, including economics, biology, and social sciences, to understand correlations and causations. For example, a scatter plot can be used to visually represent bivariate data, helping to identify trends or patterns. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Bivariate Data | Bivariate DataTopicStatistics and Probability DefinitionBivariate data involves the analysis of two variables to determine relationships between them. DescriptionBivariate data is essential in statistics as it allows for the exploration of relationships between two variables, such as height and weight. This analysis is used in various fields, including economics, biology, and social sciences, to understand correlations and causations. For example, a scatter plot can be used to visually represent bivariate data, helping to identify trends or patterns. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Bivariate Data | Bivariate DataTopicStatistics and Probability DefinitionBivariate data involves the analysis of two variables to determine relationships between them. DescriptionBivariate data is essential in statistics as it allows for the exploration of relationships between two variables, such as height and weight. This analysis is used in various fields, including economics, biology, and social sciences, to understand correlations and causations. For example, a scatter plot can be used to visually represent bivariate data, helping to identify trends or patterns. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Bivariate Data | Bivariate DataTopicStatistics and Probability DefinitionBivariate data involves the analysis of two variables to determine relationships between them. DescriptionBivariate data is essential in statistics as it allows for the exploration of relationships between two variables, such as height and weight. This analysis is used in various fields, including economics, biology, and social sciences, to understand correlations and causations. For example, a scatter plot can be used to visually represent bivariate data, helping to identify trends or patterns. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Bivariate Data | Bivariate DataTopicStatistics and Probability DefinitionBivariate data involves the analysis of two variables to determine relationships between them. DescriptionBivariate data is essential in statistics as it allows for the exploration of relationships between two variables, such as height and weight. This analysis is used in various fields, including economics, biology, and social sciences, to understand correlations and causations. For example, a scatter plot can be used to visually represent bivariate data, helping to identify trends or patterns. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Bivariate Data | Bivariate DataTopicStatistics and Probability DefinitionBivariate data involves the analysis of two variables to determine relationships between them. DescriptionBivariate data is essential in statistics as it allows for the exploration of relationships between two variables, such as height and weight. This analysis is used in various fields, including economics, biology, and social sciences, to understand correlations and causations. For example, a scatter plot can be used to visually represent bivariate data, helping to identify trends or patterns. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Causation | CausationTopicStatistics and Probability DefinitionCausation refers to the relationship between two events where one event is affected by the other. DescriptionCausation is a fundamental concept in statistics that distinguishes between correlation and causation. Understanding causation is vital in fields like medicine and social sciences to establish cause-effect relationships. For example, clinical trials are designed to establish causation between treatments and outcomes. Grasping causation is important for students to critically evaluate research findings and understand the implications of statistical analyses. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Causation | CausationTopicStatistics and Probability DefinitionCausation refers to the relationship between two events where one event is affected by the other. DescriptionCausation is a fundamental concept in statistics that distinguishes between correlation and causation. Understanding causation is vital in fields like medicine and social sciences to establish cause-effect relationships. For example, clinical trials are designed to establish causation between treatments and outcomes. Grasping causation is important for students to critically evaluate research findings and understand the implications of statistical analyses. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Causation | CausationTopicStatistics and Probability DefinitionCausation refers to the relationship between two events where one event is affected by the other. DescriptionCausation is a fundamental concept in statistics that distinguishes between correlation and causation. Understanding causation is vital in fields like medicine and social sciences to establish cause-effect relationships. For example, clinical trials are designed to establish causation between treatments and outcomes. Grasping causation is important for students to critically evaluate research findings and understand the implications of statistical analyses. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Causation | CausationTopicStatistics and Probability DefinitionCausation refers to the relationship between two events where one event is affected by the other. DescriptionCausation is a fundamental concept in statistics that distinguishes between correlation and causation. Understanding causation is vital in fields like medicine and social sciences to establish cause-effect relationships. For example, clinical trials are designed to establish causation between treatments and outcomes. Grasping causation is important for students to critically evaluate research findings and understand the implications of statistical analyses. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Causation | CausationTopicStatistics and Probability DefinitionCausation refers to the relationship between two events where one event is affected by the other. DescriptionCausation is a fundamental concept in statistics that distinguishes between correlation and causation. Understanding causation is vital in fields like medicine and social sciences to establish cause-effect relationships. For example, clinical trials are designed to establish causation between treatments and outcomes. Grasping causation is important for students to critically evaluate research findings and understand the implications of statistical analyses. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Causation | CausationTopicStatistics and Probability DefinitionCausation refers to the relationship between two events where one event is affected by the other. DescriptionCausation is a fundamental concept in statistics that distinguishes between correlation and causation. Understanding causation is vital in fields like medicine and social sciences to establish cause-effect relationships. For example, clinical trials are designed to establish causation between treatments and outcomes. Grasping causation is important for students to critically evaluate research findings and understand the implications of statistical analyses. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Combination 1 | Combination 1TopicStatistics and Probability DefinitionA combination is a selection of items from a larger pool where order does not matter. DescriptionCombinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is
where n is the total number of items, and r is the number of items to choose. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Combination 1 | Combination 1TopicStatistics and Probability DefinitionA combination is a selection of items from a larger pool where order does not matter. DescriptionCombinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is
where n is the total number of items, and r is the number of items to choose. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Combination 1 | Combination 1TopicStatistics and Probability DefinitionA combination is a selection of items from a larger pool where order does not matter. DescriptionCombinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is
where n is the total number of items, and r is the number of items to choose. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Combination 1 | Combination 1TopicStatistics and Probability DefinitionA combination is a selection of items from a larger pool where order does not matter. DescriptionCombinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is
where n is the total number of items, and r is the number of items to choose. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Combination 1 | Combination 1TopicStatistics and Probability DefinitionA combination is a selection of items from a larger pool where order does not matter. DescriptionCombinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is
where n is the total number of items, and r is the number of items to choose. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Combination 1 | Combination 1TopicStatistics and Probability DefinitionA combination is a selection of items from a larger pool where order does not matter. DescriptionCombinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is
where n is the total number of items, and r is the number of items to choose. |
Data Analysis |
|
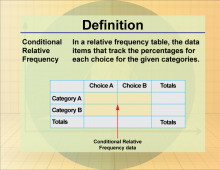
Definition--Statistics and Probability Concepts--Conditional Relative Frequency | Conditional Relative FrequencyTopicStatistics and Probability DefinitionConditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. DescriptionConditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Conditional Relative Frequency | Conditional Relative FrequencyTopicStatistics and Probability DefinitionConditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. DescriptionConditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Conditional Relative Frequency | Conditional Relative FrequencyTopicStatistics and Probability DefinitionConditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. DescriptionConditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Conditional Relative Frequency | Conditional Relative FrequencyTopicStatistics and Probability DefinitionConditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. DescriptionConditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Conditional Relative Frequency | Conditional Relative FrequencyTopicStatistics and Probability DefinitionConditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. DescriptionConditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Conditional Relative Frequency | Conditional Relative FrequencyTopicStatistics and Probability DefinitionConditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. DescriptionConditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately. |
Data Analysis |
|
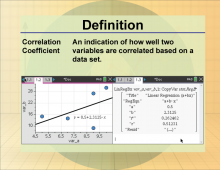
Definition--Statistics and Probability Concepts--Correlation Coefficient | Correlation CoefficientTopicStatistics and Probability DefinitionThe correlation coefficient is a measure that quantifies the degree to which two variables are related. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Correlation Coefficient | Correlation CoefficientTopicStatistics and Probability DefinitionThe correlation coefficient is a measure that quantifies the degree to which two variables are related. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Correlation Coefficient | Correlation CoefficientTopicStatistics and Probability DefinitionThe correlation coefficient is a measure that quantifies the degree to which two variables are related. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Correlation Coefficient | Correlation CoefficientTopicStatistics and Probability DefinitionThe correlation coefficient is a measure that quantifies the degree to which two variables are related. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Correlation Coefficient | Correlation CoefficientTopicStatistics and Probability DefinitionThe correlation coefficient is a measure that quantifies the degree to which two variables are related. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Correlation Coefficient | Correlation CoefficientTopicStatistics and Probability DefinitionThe correlation coefficient is a measure that quantifies the degree to which two variables are related. |
Data Analysis |
|
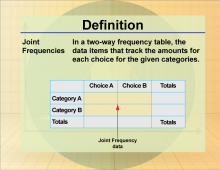
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |
|
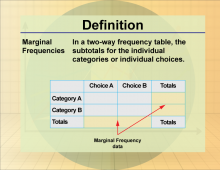
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |