
Illustrative Math Alignment: Grade 7 Unit 8
Probability and Sampling
Lesson 1: Mystery Bags
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |
|
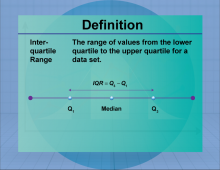
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |
|
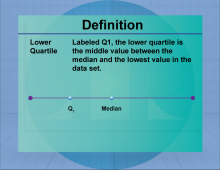
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median of an Even Data Set | Median of an Even Data SetTopicStatistics DefinitionThe median of an even data set is the mean of two of the terms. DescriptionThe Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median of an Even Data Set | Median of an Even Data SetTopicStatistics DefinitionThe median of an even data set is the mean of two of the terms. DescriptionThe Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median of an Even Data Set | Median of an Even Data SetTopicStatistics DefinitionThe median of an even data set is the mean of two of the terms. DescriptionThe Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median of an Even Data Set | Median of an Even Data SetTopicStatistics DefinitionThe median of an even data set is the mean of two of the terms. DescriptionThe Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median of an Even Data Set | Median of an Even Data SetTopicStatistics DefinitionThe median of an even data set is the mean of two of the terms. DescriptionThe Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms. |
Data Analysis |