
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 11: Equations of All Kinds of Lines
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Quizlet Flash Cards: Slope Formula, Set 04 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 05 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 06 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 07 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 08 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 09 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 10 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |
|
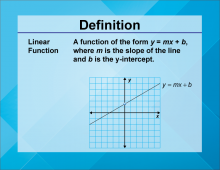
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |

|
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |

|
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |

|
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |

|
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |

|
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |
|
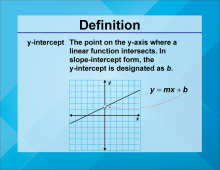
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |

|
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |

|
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |

|
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |

|
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |

|
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |
|
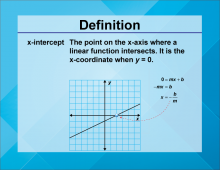
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |

|
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |

|
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |

|
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |

|
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |

|
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |
|
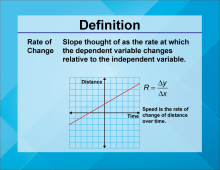
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form | Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing. |
Slope-Intercept Form |