
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 11: Equations of All Kinds of Lines
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
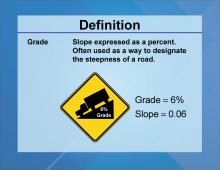
Definition--Slope Concepts--Grade | GradeTopicSlope DefinitionGrade is a ratio indicating the steepness of a slope. DescriptionThe term Grade commonly refers to the angle of elevation or slope expressed as a percentage. In engineering, grades are crucial for designing roads and railways, ensuring safety and efficiency. |
Slope |
|
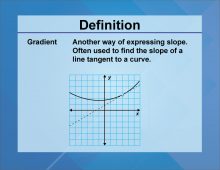
Definition--Slope Concepts--Gradient | GradientTopicSlope DefinitionGradient represents the rate of change of a quantity. DescriptionThe Gradient measures how steep a line is, calculated by the ratio of the rise to run. This concept is significant in fields like physics and economics where gradients can represent relationships between variables. |
Slope |

|
Definition--Slope Concepts--Negative Slope | Negative SlopeTopicSlope DefinitionNegative Slope indicates a decrease in value as x increases. DescriptionThe Negative Slope signifies that as one variable increases, the other decreases, often used in economics to depict inverse relationships. This term finds relevance in real-world scenarios like demand curves which slope downwards. |
Slope |

|
Definition--Slope Concepts--Pitch | PitchTopicSlope DefinitionPitch refers to the steepness of a slope in a real-world context. DescriptionPitch is commonly applied in construction and design fields to denote the angle of roofs and ramps. This is essential in architecture, especially when dealing with drainage and material use. |
Slope |

|
Definition--Slope Concepts--Point-Slope Form | Point-Slope FormTopicSlope DefinitionPoint-Slope Form is a way to express linear equations given the slope and a point on the line. DescriptionThe Point-Slope Form is crucial in algebra for identifying linear relationships given the slope and a point on the line. Understanding this concept aids in graphing lines efficiently and is foundational in higher mathematics. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Point-Slope Form |
|
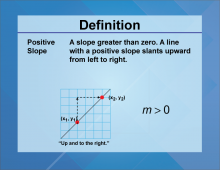
Definition--Slope Concepts--Positive Slope | Positive SlopeTopicSlope DefinitionPositive Slope indicates an increase in value as x increases. DescriptionThe Positive Slope indicates that as x grows, y also rises, signifying direct relationships in data analysis. This principle enables predictions in various analytics and trends. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |
|
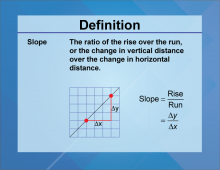
Definition--Slope Concepts--Slope | SlopeTopicSlope DefinitionSlope measures the steepness of a line. DescriptionSlope is a fundamental concept in mathematics, expressing the ratio of vertical rise to horizontal run. This is vital for understanding linear functions, essential in fields such as physics, economics, and data science. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Slope Formula | Slope FormulaTopicSlope DefinitionThe Slope Formula calculates the rate of change. DescriptionThe Slope Formula is typically represented as This formula is a cornerstone in algebra, enabling students to analyze linear equations effectively. |
Slope |

|
Definition--Slope Concepts--Slope-Intercept Form | Slope-Intercept FormTopicSlope DefinitionThe slope-intercept form is an equation of a straight line represented as y = m x + b, where m is the slope and b is the y-intercept. DescriptionThe slope-intercept form is a fundamental concept in algebra, providing a straightforward way to graph linear equations. It is widely used in various fields, from economics to physics, to model linear relationships and predict outcomes based on given data. Understanding this form is crucial for students as it lays the foundation for more complex mathematical concepts and real-world applications. |
Slope-Intercept Form |
|
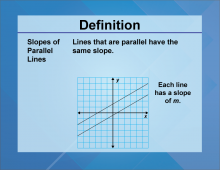
Definition--Slope Concepts--Slopes of Parallel Lines | Slopes of Parallel LinesTopicSlope DefinitionParallel lines are lines in the same plane that never meet; they have equal slopes. DescriptionUnderstanding the slopes of parallel lines is essential in geometry and algebra, as it helps in identifying and proving parallelism in shapes and graphs. This concept is applied in various fields, including architecture and engineering, where maintaining parallelism is crucial for structural integrity and design. In mathematics education, this concept aids in developing logical reasoning and problem-solving skills. |
Slope |

|
Definition--Slope Concepts--Slopes of Perpendicular Lines | Slopes of Perpendicular LinesTopicSlope DefinitionPerpendicular lines intersect at a right angle, and their slopes are negative reciprocals of each other. DescriptionThe concept of perpendicular slopes is vital in geometry, as it helps in determining the orthogonality of lines. This principle is used in various applications, such as designing perpendicular intersections in roadways and creating right-angle joints in construction. In education, it enhances students' understanding of geometric properties and their ability to solve related problems. |
Slope |

|
Definition--Slope Concepts--Steepness | SteepnessTopicSlope DefinitionSteepness is a measure of how steep a line is, typically calculated as the absolute value of the slope. DescriptionSteepness is a key concept in understanding the inclination of lines and surfaces. It is commonly used in fields like geology and civil engineering to assess the gradient of terrains and structures. In math education, learning about steepness helps students grasp the concept of slope and its practical implications, enhancing their analytical skills and understanding of real-world phenomena. |
Slope |

|
Definition--Slope Concepts--The Rise Over the Run | The Rise Over the RunTopicSlope DefinitionThe rise over the run describes the change in y over the change in x in a linear relationship. DescriptionThe concept of "rise over run" is foundational in understanding how to calculate the slope of a line. It is used in various disciplines, such as physics and economics, to model relationships and predict trends. In education, mastering this concept is crucial for students as it forms the basis for graphing linear equations and understanding the behavior of lines in a coordinate plane. |
Slope |

|
Definition--Slope Concepts--Undefined Slope | Undefined SlopeTopicSlope DefinitionUndefined slope occurs when a vertical line is present, meaning there is no change in x. DescriptionAn undefined slope is a critical concept in mathematics, particularly in graphing. It indicates a vertical line where the change in x is zero, making the slope calculation impossible. This concept is important in various fields, such as computer graphics and data analysis, where vertical lines can represent boundaries or limits. Understanding undefined slopes helps students in identifying and interpreting vertical lines in graphs. |
Slope |

|
Definition--Slope Concepts--Zero Slope | Zero SlopeTopicSlope DefinitionZero slope describes a horizontal line where there is no change in y as x changes. DescriptionA zero slope is a key concept in algebra and geometry, representing a horizontal line. It is used in various applications, such as designing flat surfaces and analyzing constant relationships in data. In education, understanding zero slopes helps students in graphing and interpreting horizontal lines, enhancing their ability to analyze linear relationships. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |

|
Desmos Activity: Slope As Rate of Change | Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost. |
Slope and Ratios and Rates |

|
Desmos Activity: Slope As Rise Over Run | Desmos Activity: Slope As Rise Over Run This Desmos activity allows students to explore slope as the ratio of the rise over the run. Click Preview to launch the activity. In the activity students click on the points to create a line segment connecting two points. Use the background grid to determine the rise and the run and calculate the slope. |
Slope |

|
Desmos Activity: Slope As Rise Over Run 2 | Desmos Activity: Slope As Rise Over Run 2 In this activity, students input different values for the coordinates to create a new line. They can then measure the rise and run to calculate the slope. |
Slope |

|
Formulas--Slope Formula | Formulas | Slope Formula
The formula for the Slope Formula. This is part of a collection of math formulas. —PRESS PREVIEW TO SEE THE IMAGE— To see the complete collection of formulas, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. What Is Slope?Watch this video to learn about the slope formula. (The transcript is also included.) |
Slope |

|
Instructional Resource--Strategy Pack--The Slope of a Line | Instructional Resource | Strategy Pack | The Slope of a Line
Learn different strategies for finding the slope of a line. The Strategy Packs provide alternate ways of solving the same problem, giving your students different approaches to the same problem. The goal of the Strategy Packs is to encourage your students to think strategically when solving math problems. —PRESS PREVIEW TO LAUNCH THE PRESENTATION— To see the complete collection of Instructional Resources, click on this link.Note: The download is a PPT file. |
Slope |

|
INSTRUCTIONAL RESOURCE: Desmos Tutorial: Linear Functions in Point-Slope Form | INSTRUCTIONAL RESOURCE: Desmos Tutorial: Linear Functions in Point-Slope Form
In this Slide Show, use the Desmos graphing calculator to explore the point-slope form. To see the complete collection of Desmos Resources click on this link. Note: The download is a PPT file. This is part of a collection of Desmos tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions, Graphs of Linear Functions and Point-Slope Form |

|
INSTRUCTIONAL RESOURCE: Math Examples 19 | INSTRUCTIONAL RESOURCE: Math Examples--Graphing Linear Functions in Slope-Intercept Form
The complete set of 13 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions and Graphs of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Math Examples 25 | INSTRUCTIONAL RESOURCE: Math Examples--Line From Two Points
The complete set of 29 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions and Graphs of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Math Examples 26 | INSTRUCTIONAL RESOURCE: Math Examples--Linear Equations in Standard Form
This PowerPoint includes the 22 Tutorials on the topic of converting Linear Equations in Standard Form to Slope-Intercept Form. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions and Graphs of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Math Examples 30 | INSTRUCTIONAL RESOURCE: Math Examples--Midpoint Formula
The complete set of 20 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Midpoint Formula |

|
INSTRUCTIONAL RESOURCE: Math Examples 36 | INSTRUCTIONAL RESOURCE: Math Examples--Point-Slope Form
The complete set of 8 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions and Graphs of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Point-Slope Form | In this Slide Show, create a template for determining the equation of a line given a point and the slope of the line. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Applications of Linear Functions, Graphs of Linear Functions and Point-Slope Form |

|
INSTRUCTIONAL RESOURCE: Tutorial: The Point-Slope Form | <h1>INSTRUCTIONAL RESOURCE: Tutorial: The Point-Slope Form</h1><p>In this Slide Show, learn about thepoint-slope form. </p><h3> This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, <a href="https://www.media4math.com/instructional-resources?field_la_display_tit… on this link.</u></strong></a> </h3> <h3> Note: The download is a PPT file. </h3>< <h2> Library of Instructional Resources </h3> |
Applications of Linear Functions, Graphs of Linear Functions and Point-Slope Form |

|
INSTRUCTIONAL RESOURCE: Tutorial: Equations of Parallel and Perpendiclar Lines (SAT Prep) | INSTRUCTIONAL RESOURCE: Tutorial: Equations of Parallel and Perpendiclar Lines (SAT Prep)
This slide show shows how to write equations in slope-intercept form for parallel and perpendicular lines. This slide show also includes some sample SAT-style questions. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Slope-Intercept Form |

|
INSTRUCTIONAL RESOURCE: Tutorial: Point-Slope Form (SAT Prep) | INSTRUCTIONAL RESOURCE: Tutorial: Point-Slope Form (SAT Prep) This slide show shows how to use the point-slope form to write a linear equation in slope-intercept form. This slide show also includes some sample SAT-style questions. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Point-Slope Form |

|
Interactive Crossword Puzzle--Slope Intercept Form | Interactive Crossword Puzzle--Slope Intercept Form
This interactive crossword puzzle tests knowledge of key terms on the topic of the slope intercept form. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Slope-Intercept Form |

|
Lesson Plan--Linear Functions and Equations (HS)--Lesson 4--Applications of Linear Functions | Lesson Plan: Applications of Linear Functions In this comprehensive lesson plan, high school students delve into the practical applications of linear functions, bridging the gap between mathematical concepts and real-world scenarios. The lesson focuses on identifying situations that can be modeled with linear equations, formulating these equations, and interpreting their components within various contexts. Key components of the lesson include: |
Slope-Intercept Form, Point-Slope Form and Standard Form |

|
Lesson Plan--Linear Functions and Equations (HS)--Lesson 4--Applications of Linear Functions | Lesson Plan: Applications of Linear Functions In this comprehensive lesson plan, high school students delve into the practical applications of linear functions, bridging the gap between mathematical concepts and real-world scenarios. The lesson focuses on identifying situations that can be modeled with linear equations, formulating these equations, and interpreting their components within various contexts. Key components of the lesson include: |
Slope-Intercept Form, Point-Slope Form and Standard Form |

|
Lesson Plan--Linear Functions and Equations (HS)--Lesson 4--Applications of Linear Functions | Lesson Plan: Applications of Linear Functions In this comprehensive lesson plan, high school students delve into the practical applications of linear functions, bridging the gap between mathematical concepts and real-world scenarios. The lesson focuses on identifying situations that can be modeled with linear equations, formulating these equations, and interpreting their components within various contexts. Key components of the lesson include: |
Slope-Intercept Form, Point-Slope Form and Standard Form |

|
Lesson Plan--Linear Functions and Equations (MS)--Lesson 1--Introduction to Linear Equations | Lesson Plan: Introduction to Linear EquationsThis lesson is the first in a five-part series on linear equations for middle school students. It introduces the fundamental concepts of linear equations, their structure, and their applications in real-world contexts. |
Slope-Intercept Form and Standard Form |

|
Lesson Plan--Linear Functions and Equations (MS)--Lesson 1--Introduction to Linear Equations | Lesson Plan: Introduction to Linear EquationsThis lesson is the first in a five-part series on linear equations for middle school students. It introduces the fundamental concepts of linear equations, their structure, and their applications in real-world contexts. |
Slope-Intercept Form and Standard Form |

|
Lesson Plan--Linear Functions and Equations (MS)--Lesson 2--Graphing Linear Equations | Lesson Plan: Graphing Linear EquationsThis is the second lesson in a five-part series on linear equations. It introduces students to graphing linear equations using slope-intercept form: y=mx+b. Students will learn to identify slope and y-intercept, plot points, and interpret graphs in real-world contexts. The lesson aligns with Common Core Standards 8.EE.B.5 and 8.EE.B.6. |
Graphs of Linear Functions |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 8)--Lesson 5--Analyzing and Comparing Linear Relationships, Including Parallel and Perpendicular Lines | Lesson Plan: Parallel and Perpendicular Lines In this lesson, students explore the properties of parallel and perpendicular lines in coordinate geometry. They will learn how to identify these lines based on their slopes, determine equations for parallel and perpendicular lines, and apply these concepts to solve real-world and mathematical problems. Key concepts covered in this lesson include: |
Graphs of Linear Functions |

|
Lesson Plan--Slope Concepts--Lesson 1--What Is Slope? | Lesson Plan: What Is Slope? This lesson is the first in a six-part series designed to introduce middle school students to the concept of slope. Through interactive digital resources from Media4Math, students will explore how slope represents the ratio of vertical change to horizontal change between two points on a line. Key learning objectives include: Defining slope as a ratio of rise over run.Interpreting slope in real-world scenarios, such as staircases and ramps.Calculating slope using coordinate points on a graph.The lesson includes engaging digital media, practice problems, and guided activities to help students develop a strong conceptual understanding. This resource is aligned with educational standards, making it an essential part of any middle school math curriculum. Subscribers to Media4Math can download PDF versions of the lesson plan for easy classroom use. |
Slope |

|
Lesson Plan--Slope Concepts--Lesson 2--Slope and Similar Triangles | Lesson Plan: Slope and Similar Triangles This lesson is the second installment in Media4Math's comprehensive six-part series on understanding slope in mathematics. It explores the relationship between slope and similar triangles, providing students with a geometric perspective on why the slope between any two distinct points on a non-vertical line remains constant. |
Slope |

|
Lesson Plan--Slope Concepts--Lesson 3--Visualizing Slope | Lesson Plan: Visualizing Slope on a Graph This lesson is the third installment in Media4Math's comprehensive six-part series on understanding slope in mathematics. It focuses on helping students visualize and comprehend slope by engaging in hands-on activities that involve plotting points on a coordinate plane and analyzing the resulting lines. |
Slope |

|
Lesson Plan--Slope Concepts--Lesson 4--Types of Slope | Lesson Plan: Types of Slope This lesson is the fourth installment in Media4Math's comprehensive six-part series on understanding slope in mathematics. It focuses on helping students differentiate among the four types of slope: positive, negative, zero, and undefined. Through interactive activities and visual aids, students will analyze how each type of slope affects the direction of a line on a graph. |
Slope |

|
Lesson Plan--Slope Concepts--Lesson 5--The Slope Formula | Lesson Plan: The Slope Formula This lesson is the fifth installment in Media4Math's comprehensive six-part series on understanding slope in mathematics. It introduces students to the slope formula, a fundamental tool in algebra for determining the steepness and direction of a line between two points on a coordinate plane. |
Slope |
|
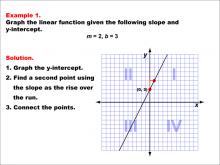
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 1 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 1TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of 2 and a y-intercept of 3. The process involves three key steps: first, plotting the y-intercept at (0, 3); second, using the slope to find another point on the line; and finally, connecting these points to form the line. |
Slope-Intercept Form |
|
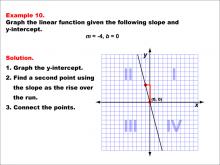
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 10 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 10TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of -4 and a y-intercept of 0. The method involves three main steps: plotting the y-intercept at the origin (0, 0), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |