Illustrative Math Alignment: Grade 8 Unit 3

Linear Relationships

Lesson 11: Equations of All Kinds of Lines

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form	Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form Topic Linear Functions Description The term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing.	Slope-Intercept Form
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form	Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form Topic Linear Functions Description The term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing.	Slope-Intercept Form
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form	Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form Topic Linear Functions Description The term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing.	Slope-Intercept Form
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form	Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form Topic Linear Functions Description The term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing.	Slope-Intercept Form
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form	Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form Topic Linear Functions Description The term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing.	Slope-Intercept Form
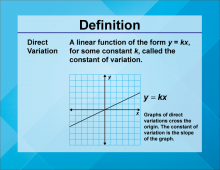
Video Definition 17--Linear Function Concepts--Direct Variation	Video Definition 17--Linear Function Concepts--Direct Variation Topic Linear Functions Description The term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics.	Slope-Intercept Form
Video Definition 17--Linear Function Concepts--Direct Variation	Video Definition 17--Linear Function Concepts--Direct Variation Topic Linear Functions Description The term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics.	Slope-Intercept Form
Video Definition 17--Linear Function Concepts--Direct Variation	Video Definition 17--Linear Function Concepts--Direct Variation Topic Linear Functions Description The term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics.	Slope-Intercept Form
Video Definition 17--Linear Function Concepts--Direct Variation	Video Definition 17--Linear Function Concepts--Direct Variation Topic Linear Functions Description The term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics.	Slope-Intercept Form
Video Definition 17--Linear Function Concepts--Direct Variation	Video Definition 17--Linear Function Concepts--Direct Variation Topic Linear Functions Description The term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics.	Slope-Intercept Form
Video Definition 17--Linear Function Concepts--Direct Variation	Video Definition 17--Linear Function Concepts--Direct Variation Topic Linear Functions Description The term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics.	Slope-Intercept Form
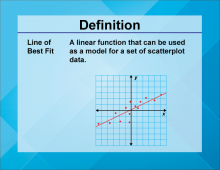
Video Definition 18--Linear Function Concepts--Line of Best Fit	Video Definition 18--Linear Function Concepts--Line of Best Fit Topic Linear Functions Description The term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends.	Graphs of Linear Functions
Video Definition 18--Linear Function Concepts--Line of Best Fit	Video Definition 18--Linear Function Concepts--Line of Best Fit Topic Linear Functions Description The term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends.	Graphs of Linear Functions
Video Definition 18--Linear Function Concepts--Line of Best Fit	Video Definition 18--Linear Function Concepts--Line of Best Fit Topic Linear Functions Description The term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends.	Graphs of Linear Functions
Video Definition 18--Linear Function Concepts--Line of Best Fit	Video Definition 18--Linear Function Concepts--Line of Best Fit Topic Linear Functions Description The term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends.	Graphs of Linear Functions
Video Definition 18--Linear Function Concepts--Line of Best Fit	Video Definition 18--Linear Function Concepts--Line of Best Fit Topic Linear Functions Description The term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends.	Graphs of Linear Functions
Video Definition 18--Linear Function Concepts--Line of Best Fit	Video Definition 18--Linear Function Concepts--Line of Best Fit Topic Linear Functions Description The term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends.	Graphs of Linear Functions
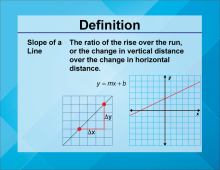
Video Definition 19--Linear Function Concepts--Slope	Video Definition 19--Linear Function Concepts--Slope Topic Linear Functions Description The term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction.	Slope
Video Definition 19--Linear Function Concepts--Slope	Video Definition 19--Linear Function Concepts--Slope Topic Linear Functions Description The term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction.	Slope
Video Definition 19--Linear Function Concepts--Slope	Video Definition 19--Linear Function Concepts--Slope Topic Linear Functions Description The term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction.	Slope
Video Definition 19--Linear Function Concepts--Slope	Video Definition 19--Linear Function Concepts--Slope Topic Linear Functions Description The term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction.	Slope
Video Definition 19--Linear Function Concepts--Slope	Video Definition 19--Linear Function Concepts--Slope Topic Linear Functions Description The term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction.	Slope
Video Definition 19--Linear Function Concepts--Slope	Video Definition 19--Linear Function Concepts--Slope Topic Linear Functions Description The term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction.	Slope
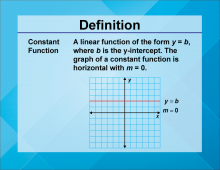
Video Definition 2--Linear Function Concepts--Constant Function	Video Definition 2--Linear Function Concepts--Constant Function Topic Linear Functions Description The term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines.	Slope-Intercept Form
Video Definition 2--Linear Function Concepts--Constant Function	Video Definition 2--Linear Function Concepts--Constant Function Topic Linear Functions Description The term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines.	Slope-Intercept Form
Video Definition 2--Linear Function Concepts--Constant Function	Video Definition 2--Linear Function Concepts--Constant Function Topic Linear Functions Description The term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines.	Slope-Intercept Form
Video Definition 2--Linear Function Concepts--Constant Function	Video Definition 2--Linear Function Concepts--Constant Function Topic Linear Functions Description The term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines.	Slope-Intercept Form
Video Definition 2--Linear Function Concepts--Constant Function	Video Definition 2--Linear Function Concepts--Constant Function Topic Linear Functions Description The term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines.	Slope-Intercept Form
Video Definition 2--Linear Function Concepts--Constant Function	Video Definition 2--Linear Function Concepts--Constant Function Topic Linear Functions Description The term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines.	Slope-Intercept Form
Video Definition 20--Linear Function Concepts--System of Linear Equations	Video Definition 20--Linear Function Concepts--System of Linear Equations Topic Linear Functions Description The term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving.	Applications of Linear Functions and Graphs of Linear Functions
Video Definition 20--Linear Function Concepts--System of Linear Equations	Video Definition 20--Linear Function Concepts--System of Linear Equations Topic Linear Functions Description The term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving.	Applications of Linear Functions and Graphs of Linear Functions
Video Definition 20--Linear Function Concepts--System of Linear Equations	Video Definition 20--Linear Function Concepts--System of Linear Equations Topic Linear Functions Description The term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving.	Applications of Linear Functions and Graphs of Linear Functions
Video Definition 20--Linear Function Concepts--System of Linear Equations	Video Definition 20--Linear Function Concepts--System of Linear Equations Topic Linear Functions Description The term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving.	Applications of Linear Functions and Graphs of Linear Functions
Video Definition 20--Linear Function Concepts--System of Linear Equations	Video Definition 20--Linear Function Concepts--System of Linear Equations Topic Linear Functions Description The term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving.	Applications of Linear Functions and Graphs of Linear Functions
Video Definition 20--Linear Function Concepts--System of Linear Equations	Video Definition 20--Linear Function Concepts--System of Linear Equations Topic Linear Functions Description The term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving.	Applications of Linear Functions and Graphs of Linear Functions
Video Definition 21--Linear Function Concepts--Solution to a Linear Equation	Video Definition 21--Linear Function Concepts--Solution to a Linear Equation Topic Linear Functions Description The term is "Solution to a Linear Equation," defined as finding the value(s) of a variable that make the equation true. An example includes solving 2x + 5 = 15 step-by-step to find x = 5. This term explains how linear equations are solved, demonstrating the logical process of isolating variables.	Solving Systems of Equations
Video Definition 21--Linear Function Concepts--Solution to a Linear Equation	Video Definition 21--Linear Function Concepts--Solution to a Linear Equation Topic Linear Functions Description The term is "Solution to a Linear Equation," defined as finding the value(s) of a variable that make the equation true. An example includes solving 2x + 5 = 15 step-by-step to find x = 5. This term explains how linear equations are solved, demonstrating the logical process of isolating variables.	Solving Systems of Equations
Video Definition 21--Linear Function Concepts--Solution to a Linear Equation	Video Definition 21--Linear Function Concepts--Solution to a Linear Equation Topic Linear Functions Description The term is "Solution to a Linear Equation," defined as finding the value(s) of a variable that make the equation true. An example includes solving 2x + 5 = 15 step-by-step to find x = 5. This term explains how linear equations are solved, demonstrating the logical process of isolating variables.	Solving Systems of Equations
Video Definition 21--Linear Function Concepts--Solution to a Linear Equation	Video Definition 21--Linear Function Concepts--Solution to a Linear Equation Topic Linear Functions Description The term is "Solution to a Linear Equation," defined as finding the value(s) of a variable that make the equation true. An example includes solving 2x + 5 = 15 step-by-step to find x = 5. This term explains how linear equations are solved, demonstrating the logical process of isolating variables.	Solving Systems of Equations
Video Definition 21--Linear Function Concepts--Solution to a Linear Equation	Video Definition 21--Linear Function Concepts--Solution to a Linear Equation Topic Linear Functions Description The term is "Solution to a Linear Equation," defined as finding the value(s) of a variable that make the equation true. An example includes solving 2x + 5 = 15 step-by-step to find x = 5. This term explains how linear equations are solved, demonstrating the logical process of isolating variables.	Solving Systems of Equations

Illustrative Math Alignment: Grade 8 Unit 3

Linear Relationships

Lesson 11: Equations of All Kinds of Lines

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic