
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 11: Equations of All Kinds of Lines
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
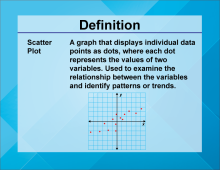
Video Definition 23--Linear Function Concepts--Scatter Plot | Video Definition 23--Linear Function Concepts--Scatter Plot
TopicLinear Functions DescriptionThe term is "Scatter Plot," defined as a graph displaying individual data points as dots, where each dot represents the values of two variables. Used to examine relationships and identify patterns or trends. This term provides a graphical tool to visualize and analyze linear relationships in data. |
Data Analysis |

|
Video Definition 23--Linear Function Concepts--Scatter Plot | Video Definition 23--Linear Function Concepts--Scatter Plot
TopicLinear Functions DescriptionThe term is "Scatter Plot," defined as a graph displaying individual data points as dots, where each dot represents the values of two variables. Used to examine relationships and identify patterns or trends. This term provides a graphical tool to visualize and analyze linear relationships in data. |
Data Analysis |

|
Video Definition 23--Linear Function Concepts--Scatter Plot | Video Definition 23--Linear Function Concepts--Scatter Plot
TopicLinear Functions DescriptionThe term is "Scatter Plot," defined as a graph displaying individual data points as dots, where each dot represents the values of two variables. Used to examine relationships and identify patterns or trends. This term provides a graphical tool to visualize and analyze linear relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |
|
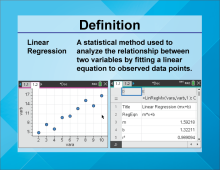
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |

|
Video Definition 27--Linear Function Concepts--Linear Expression | Video Definition 27--Linear Function Concepts--Linear Expression
TopicLinear Functions DescriptionThe term is "Linear Expression," defined as an algebraic expression consisting of at least one term where the variable has an exponent of 1. Examples include x, 2x - 3, and -4x + 8. This term establishes the foundation of linear algebra by focusing on the simplest forms of linear relationships. |
Variable Expressions |

|
Video Definition 27--Linear Function Concepts--Linear Expression | Video Definition 27--Linear Function Concepts--Linear Expression
TopicLinear Functions DescriptionThe term is "Linear Expression," defined as an algebraic expression consisting of at least one term where the variable has an exponent of 1. Examples include x, 2x - 3, and -4x + 8. This term establishes the foundation of linear algebra by focusing on the simplest forms of linear relationships. |
Variable Expressions |

|
Video Definition 27--Linear Function Concepts--Linear Expression | Video Definition 27--Linear Function Concepts--Linear Expression
TopicLinear Functions DescriptionThe term is "Linear Expression," defined as an algebraic expression consisting of at least one term where the variable has an exponent of 1. Examples include x, 2x - 3, and -4x + 8. This term establishes the foundation of linear algebra by focusing on the simplest forms of linear relationships. |
Variable Expressions |

|
Video Definition 27--Linear Function Concepts--Linear Expression | Video Definition 27--Linear Function Concepts--Linear Expression
TopicLinear Functions DescriptionThe term is "Linear Expression," defined as an algebraic expression consisting of at least one term where the variable has an exponent of 1. Examples include x, 2x - 3, and -4x + 8. This term establishes the foundation of linear algebra by focusing on the simplest forms of linear relationships. |
Variable Expressions |

|
Video Definition 27--Linear Function Concepts--Linear Expression | Video Definition 27--Linear Function Concepts--Linear Expression
TopicLinear Functions DescriptionThe term is "Linear Expression," defined as an algebraic expression consisting of at least one term where the variable has an exponent of 1. Examples include x, 2x - 3, and -4x + 8. This term establishes the foundation of linear algebra by focusing on the simplest forms of linear relationships. |
Variable Expressions |

|
Video Definition 27--Linear Function Concepts--Linear Expression | Video Definition 27--Linear Function Concepts--Linear Expression
TopicLinear Functions DescriptionThe term is "Linear Expression," defined as an algebraic expression consisting of at least one term where the variable has an exponent of 1. Examples include x, 2x - 3, and -4x + 8. This term establishes the foundation of linear algebra by focusing on the simplest forms of linear relationships. |
Variable Expressions |

|
Video Definition 28--Linear Function Concepts--Inverse of a Linear Function | Video Definition 28--Linear Function Concepts--Inverse of a Linear Function
TopicLinear Functions DescriptionThe term is "Inverse of a Linear Function," defined as the function f-1(x) such that its graph is the mirror image of f(x) across the line y = x. An example is f(x) = -3x + 3 and its inverse f-1(x) = -1/3 * x + 1. This term introduces the concept of function inverses, showing symmetry in linear functions. |
Functions and Their Inverses |

|
Video Definition 28--Linear Function Concepts--Inverse of a Linear Function | Video Definition 28--Linear Function Concepts--Inverse of a Linear Function
TopicLinear Functions DescriptionThe term is "Inverse of a Linear Function," defined as the function f-1(x) such that its graph is the mirror image of f(x) across the line y = x. An example is f(x) = -3x + 3 and its inverse f-1(x) = -1/3 * x + 1. This term introduces the concept of function inverses, showing symmetry in linear functions. |
Functions and Their Inverses |

|
Video Definition 28--Linear Function Concepts--Inverse of a Linear Function | Video Definition 28--Linear Function Concepts--Inverse of a Linear Function
TopicLinear Functions DescriptionThe term is "Inverse of a Linear Function," defined as the function f-1(x) such that its graph is the mirror image of f(x) across the line y = x. An example is f(x) = -3x + 3 and its inverse f-1(x) = -1/3 * x + 1. This term introduces the concept of function inverses, showing symmetry in linear functions. |
Functions and Their Inverses |

|
Video Definition 28--Linear Function Concepts--Inverse of a Linear Function | Video Definition 28--Linear Function Concepts--Inverse of a Linear Function
TopicLinear Functions DescriptionThe term is "Inverse of a Linear Function," defined as the function f-1(x) such that its graph is the mirror image of f(x) across the line y = x. An example is f(x) = -3x + 3 and its inverse f-1(x) = -1/3 * x + 1. This term introduces the concept of function inverses, showing symmetry in linear functions. |
Functions and Their Inverses |

|
Video Definition 28--Linear Function Concepts--Inverse of a Linear Function | Video Definition 28--Linear Function Concepts--Inverse of a Linear Function
TopicLinear Functions DescriptionThe term is "Inverse of a Linear Function," defined as the function f-1(x) such that its graph is the mirror image of f(x) across the line y = x. An example is f(x) = -3x + 3 and its inverse f-1(x) = -1/3 * x + 1. This term introduces the concept of function inverses, showing symmetry in linear functions. |
Functions and Their Inverses |

|
Video Definition 28--Linear Function Concepts--Inverse of a Linear Function | Video Definition 28--Linear Function Concepts--Inverse of a Linear Function
TopicLinear Functions DescriptionThe term is "Inverse of a Linear Function," defined as the function f-1(x) such that its graph is the mirror image of f(x) across the line y = x. An example is f(x) = -3x + 3 and its inverse f-1(x) = -1/3 * x + 1. This term introduces the concept of function inverses, showing symmetry in linear functions. |
Functions and Their Inverses |

|
Video Definition 29--Linear Function Concepts--Piecewise Linear Functions | Video Definition 29--Linear Function Concepts--Piecewise Linear Functions
TopicLinear Functions DescriptionThe term is "Piecewise Linear Functions," defined as special functions composed of linear function segments. Examples include step functions and absolute value functions. This term extends the scope of linear functions to piecewise and segmented applications, showcasing broader versatility. |
Special Functions |

|
Video Definition 29--Linear Function Concepts--Piecewise Linear Functions | Video Definition 29--Linear Function Concepts--Piecewise Linear Functions
TopicLinear Functions DescriptionThe term is "Piecewise Linear Functions," defined as special functions composed of linear function segments. Examples include step functions and absolute value functions. This term extends the scope of linear functions to piecewise and segmented applications, showcasing broader versatility. |
Special Functions |

|
Video Definition 29--Linear Function Concepts--Piecewise Linear Functions | Video Definition 29--Linear Function Concepts--Piecewise Linear Functions
TopicLinear Functions DescriptionThe term is "Piecewise Linear Functions," defined as special functions composed of linear function segments. Examples include step functions and absolute value functions. This term extends the scope of linear functions to piecewise and segmented applications, showcasing broader versatility. |
Special Functions |

|
Video Definition 29--Linear Function Concepts--Piecewise Linear Functions | Video Definition 29--Linear Function Concepts--Piecewise Linear Functions
TopicLinear Functions DescriptionThe term is "Piecewise Linear Functions," defined as special functions composed of linear function segments. Examples include step functions and absolute value functions. This term extends the scope of linear functions to piecewise and segmented applications, showcasing broader versatility. |
Special Functions |

|
Video Definition 29--Linear Function Concepts--Piecewise Linear Functions | Video Definition 29--Linear Function Concepts--Piecewise Linear Functions
TopicLinear Functions DescriptionThe term is "Piecewise Linear Functions," defined as special functions composed of linear function segments. Examples include step functions and absolute value functions. This term extends the scope of linear functions to piecewise and segmented applications, showcasing broader versatility. |
Special Functions |

|
Video Definition 29--Linear Function Concepts--Piecewise Linear Functions | Video Definition 29--Linear Function Concepts--Piecewise Linear Functions
TopicLinear Functions DescriptionThe term is "Piecewise Linear Functions," defined as special functions composed of linear function segments. Examples include step functions and absolute value functions. This term extends the scope of linear functions to piecewise and segmented applications, showcasing broader versatility. |
Special Functions |
|
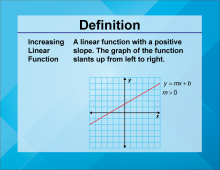
Video Definition 3--Linear Function Concepts--Increasing Linear Function | Video Definition 3--Linear Function Concepts--Increasing Linear Function
TopicLinear Functions DescriptionThe term is "Increasing Linear Function," defined as a linear function with a positive slope. The graph of the function slants up from left to right, represented as y = mx + b with m > 0. This term complements the concept of decreasing linear functions by focusing on positive slope behavior. |
Slope-Intercept Form |

|
Video Definition 3--Linear Function Concepts--Increasing Linear Function | Video Definition 3--Linear Function Concepts--Increasing Linear Function
TopicLinear Functions DescriptionThe term is "Increasing Linear Function," defined as a linear function with a positive slope. The graph of the function slants up from left to right, represented as y = mx + b with m > 0. This term complements the concept of decreasing linear functions by focusing on positive slope behavior. |
Slope-Intercept Form |

|
Video Definition 3--Linear Function Concepts--Increasing Linear Function | Video Definition 3--Linear Function Concepts--Increasing Linear Function
TopicLinear Functions DescriptionThe term is "Increasing Linear Function," defined as a linear function with a positive slope. The graph of the function slants up from left to right, represented as y = mx + b with m > 0. This term complements the concept of decreasing linear functions by focusing on positive slope behavior. |
Slope-Intercept Form |

|
Video Definition 3--Linear Function Concepts--Increasing Linear Function | Video Definition 3--Linear Function Concepts--Increasing Linear Function
TopicLinear Functions DescriptionThe term is "Increasing Linear Function," defined as a linear function with a positive slope. The graph of the function slants up from left to right, represented as y = mx + b with m > 0. This term complements the concept of decreasing linear functions by focusing on positive slope behavior. |
Slope-Intercept Form |

|
Video Definition 3--Linear Function Concepts--Increasing Linear Function | Video Definition 3--Linear Function Concepts--Increasing Linear Function
TopicLinear Functions DescriptionThe term is "Increasing Linear Function," defined as a linear function with a positive slope. The graph of the function slants up from left to right, represented as y = mx + b with m > 0. This term complements the concept of decreasing linear functions by focusing on positive slope behavior. |
Slope-Intercept Form |

|
Video Definition 3--Linear Function Concepts--Increasing Linear Function | Video Definition 3--Linear Function Concepts--Increasing Linear Function
TopicLinear Functions DescriptionThe term is "Increasing Linear Function," defined as a linear function with a positive slope. The graph of the function slants up from left to right, represented as y = mx + b with m > 0. This term complements the concept of decreasing linear functions by focusing on positive slope behavior. |
Slope-Intercept Form |

|
Video Definition 30--Linear Function Concepts--Discrete Linear Functions | Video Definition 30--Linear Function Concepts--Discrete Linear Functions
TopicLinear Functions DescriptionThe term is "Discrete Linear Functions," defined as discontinuous functions made up of linear function parts. Examples include step functions, illustrated with a piecewise graph. This term extends the concept of linearity to piecewise or segmented functions, bridging the gap between continuous and discrete representations. |
Special Functions |

|
Video Definition 30--Linear Function Concepts--Discrete Linear Functions | Video Definition 30--Linear Function Concepts--Discrete Linear Functions
TopicLinear Functions DescriptionThe term is "Discrete Linear Functions," defined as discontinuous functions made up of linear function parts. Examples include step functions, illustrated with a piecewise graph. This term extends the concept of linearity to piecewise or segmented functions, bridging the gap between continuous and discrete representations. |
Special Functions |

|
Video Definition 30--Linear Function Concepts--Discrete Linear Functions | Video Definition 30--Linear Function Concepts--Discrete Linear Functions
TopicLinear Functions DescriptionThe term is "Discrete Linear Functions," defined as discontinuous functions made up of linear function parts. Examples include step functions, illustrated with a piecewise graph. This term extends the concept of linearity to piecewise or segmented functions, bridging the gap between continuous and discrete representations. |
Special Functions |

|
Video Definition 30--Linear Function Concepts--Discrete Linear Functions | Video Definition 30--Linear Function Concepts--Discrete Linear Functions
TopicLinear Functions DescriptionThe term is "Discrete Linear Functions," defined as discontinuous functions made up of linear function parts. Examples include step functions, illustrated with a piecewise graph. This term extends the concept of linearity to piecewise or segmented functions, bridging the gap between continuous and discrete representations. |
Special Functions |

|
Video Definition 30--Linear Function Concepts--Discrete Linear Functions | Video Definition 30--Linear Function Concepts--Discrete Linear Functions
TopicLinear Functions DescriptionThe term is "Discrete Linear Functions," defined as discontinuous functions made up of linear function parts. Examples include step functions, illustrated with a piecewise graph. This term extends the concept of linearity to piecewise or segmented functions, bridging the gap between continuous and discrete representations. |
Special Functions |