
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 11: Equations of All Kinds of Lines
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Video Definition 30--Linear Function Concepts--Discrete Linear Functions | Video Definition 30--Linear Function Concepts--Discrete Linear Functions
TopicLinear Functions DescriptionThe term is "Discrete Linear Functions," defined as discontinuous functions made up of linear function parts. Examples include step functions, illustrated with a piecewise graph. This term extends the concept of linearity to piecewise or segmented functions, bridging the gap between continuous and discrete representations. |
Special Functions |
|
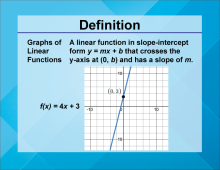
Video Definition 31--Linear Function Concepts--Graph of a Linear Function | Video Definition 31--Linear Function Concepts--Graph of a Linear Function
TopicLinear Functions DescriptionThe term is "Graphs of Linear Functions," defined as a linear function in slope-intercept form y = mx + b that crosses the y-axis at (0, b) and has a slope of m. An example graph shows f(x) = 4x + 3 crossing the y-axis at (0, 3). This term visualizes how linear functions are represented on a graph, providing insight into slope and y-intercept properties. |
Graphs of Linear Functions |

|
Video Definition 31--Linear Function Concepts--Graph of a Linear Function | Video Definition 31--Linear Function Concepts--Graph of a Linear Function
TopicLinear Functions DescriptionThe term is "Graphs of Linear Functions," defined as a linear function in slope-intercept form y = mx + b that crosses the y-axis at (0, b) and has a slope of m. An example graph shows f(x) = 4x + 3 crossing the y-axis at (0, 3). This term visualizes how linear functions are represented on a graph, providing insight into slope and y-intercept properties. |
Graphs of Linear Functions |

|
Video Definition 31--Linear Function Concepts--Graph of a Linear Function | Video Definition 31--Linear Function Concepts--Graph of a Linear Function
TopicLinear Functions DescriptionThe term is "Graphs of Linear Functions," defined as a linear function in slope-intercept form y = mx + b that crosses the y-axis at (0, b) and has a slope of m. An example graph shows f(x) = 4x + 3 crossing the y-axis at (0, 3). This term visualizes how linear functions are represented on a graph, providing insight into slope and y-intercept properties. |
Graphs of Linear Functions |

|
Video Definition 31--Linear Function Concepts--Graph of a Linear Function | Video Definition 31--Linear Function Concepts--Graph of a Linear Function
TopicLinear Functions DescriptionThe term is "Graphs of Linear Functions," defined as a linear function in slope-intercept form y = mx + b that crosses the y-axis at (0, b) and has a slope of m. An example graph shows f(x) = 4x + 3 crossing the y-axis at (0, 3). This term visualizes how linear functions are represented on a graph, providing insight into slope and y-intercept properties. |
Graphs of Linear Functions |

|
Video Definition 31--Linear Function Concepts--Graph of a Linear Function | Video Definition 31--Linear Function Concepts--Graph of a Linear Function
TopicLinear Functions DescriptionThe term is "Graphs of Linear Functions," defined as a linear function in slope-intercept form y = mx + b that crosses the y-axis at (0, b) and has a slope of m. An example graph shows f(x) = 4x + 3 crossing the y-axis at (0, 3). This term visualizes how linear functions are represented on a graph, providing insight into slope and y-intercept properties. |
Graphs of Linear Functions |

|
Video Definition 31--Linear Function Concepts--Graph of a Linear Function | Video Definition 31--Linear Function Concepts--Graph of a Linear Function
TopicLinear Functions DescriptionThe term is "Graphs of Linear Functions," defined as a linear function in slope-intercept form y = mx + b that crosses the y-axis at (0, b) and has a slope of m. An example graph shows f(x) = 4x + 3 crossing the y-axis at (0, 3). This term visualizes how linear functions are represented on a graph, providing insight into slope and y-intercept properties. |
Graphs of Linear Functions |

|
Video Definition 32--Linear Function Concepts--Linear Binomial | Video Definition 32--Linear Function Concepts--Linear Binomial
TopicLinear Functions DescriptionThe term is "Linear Binomial," defined as a linear polynomial consisting of two terms. Examples include x + 1, -3x + 2, and (x + 2)(x - 2) = x^2 - 4, demonstrating how linear binomials can factor into higher-order polynomials. This term builds on linear expressions by focusing on binomial cases, important for algebraic manipulation. |
Polynomial Expressions |

|
Video Definition 32--Linear Function Concepts--Linear Binomial | Video Definition 32--Linear Function Concepts--Linear Binomial
TopicLinear Functions DescriptionThe term is "Linear Binomial," defined as a linear polynomial consisting of two terms. Examples include x + 1, -3x + 2, and (x + 2)(x - 2) = x^2 - 4, demonstrating how linear binomials can factor into higher-order polynomials. This term builds on linear expressions by focusing on binomial cases, important for algebraic manipulation. |
Polynomial Expressions |

|
Video Definition 32--Linear Function Concepts--Linear Binomial | Video Definition 32--Linear Function Concepts--Linear Binomial
TopicLinear Functions DescriptionThe term is "Linear Binomial," defined as a linear polynomial consisting of two terms. Examples include x + 1, -3x + 2, and (x + 2)(x - 2) = x^2 - 4, demonstrating how linear binomials can factor into higher-order polynomials. This term builds on linear expressions by focusing on binomial cases, important for algebraic manipulation. |
Polynomial Expressions |

|
Video Definition 32--Linear Function Concepts--Linear Binomial | Video Definition 32--Linear Function Concepts--Linear Binomial
TopicLinear Functions DescriptionThe term is "Linear Binomial," defined as a linear polynomial consisting of two terms. Examples include x + 1, -3x + 2, and (x + 2)(x - 2) = x^2 - 4, demonstrating how linear binomials can factor into higher-order polynomials. This term builds on linear expressions by focusing on binomial cases, important for algebraic manipulation. |
Polynomial Expressions |

|
Video Definition 32--Linear Function Concepts--Linear Binomial | Video Definition 32--Linear Function Concepts--Linear Binomial
TopicLinear Functions DescriptionThe term is "Linear Binomial," defined as a linear polynomial consisting of two terms. Examples include x + 1, -3x + 2, and (x + 2)(x - 2) = x^2 - 4, demonstrating how linear binomials can factor into higher-order polynomials. This term builds on linear expressions by focusing on binomial cases, important for algebraic manipulation. |
Polynomial Expressions |

|
Video Definition 32--Linear Function Concepts--Linear Binomial | Video Definition 32--Linear Function Concepts--Linear Binomial
TopicLinear Functions DescriptionThe term is "Linear Binomial," defined as a linear polynomial consisting of two terms. Examples include x + 1, -3x + 2, and (x + 2)(x - 2) = x^2 - 4, demonstrating how linear binomials can factor into higher-order polynomials. This term builds on linear expressions by focusing on binomial cases, important for algebraic manipulation. |
Polynomial Expressions |

|
Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term | Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term
TopicLinear Functions DescriptionThe term is "Coefficient of the Linear Term," defined as the numerical factor of the variable in a linear expression, equation, or function. Examples provided include x + 3, where the coefficient is 1; y = -3x + 4, where the coefficient is -3; and 7x - 6 = 15, where the coefficient is 7. This term introduces the concept of coefficients in linear expressions, forming the foundation for understanding how variables scale in linear equations. |
Variable Expressions |

|
Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term | Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term
TopicLinear Functions DescriptionThe term is "Coefficient of the Linear Term," defined as the numerical factor of the variable in a linear expression, equation, or function. Examples provided include x + 3, where the coefficient is 1; y = -3x + 4, where the coefficient is -3; and 7x - 6 = 15, where the coefficient is 7. This term introduces the concept of coefficients in linear expressions, forming the foundation for understanding how variables scale in linear equations. |
Variable Expressions |

|
Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term | Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term
TopicLinear Functions DescriptionThe term is "Coefficient of the Linear Term," defined as the numerical factor of the variable in a linear expression, equation, or function. Examples provided include x + 3, where the coefficient is 1; y = -3x + 4, where the coefficient is -3; and 7x - 6 = 15, where the coefficient is 7. This term introduces the concept of coefficients in linear expressions, forming the foundation for understanding how variables scale in linear equations. |
Variable Expressions |

|
Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term | Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term
TopicLinear Functions DescriptionThe term is "Coefficient of the Linear Term," defined as the numerical factor of the variable in a linear expression, equation, or function. Examples provided include x + 3, where the coefficient is 1; y = -3x + 4, where the coefficient is -3; and 7x - 6 = 15, where the coefficient is 7. This term introduces the concept of coefficients in linear expressions, forming the foundation for understanding how variables scale in linear equations. |
Variable Expressions |

|
Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term | Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term
TopicLinear Functions DescriptionThe term is "Coefficient of the Linear Term," defined as the numerical factor of the variable in a linear expression, equation, or function. Examples provided include x + 3, where the coefficient is 1; y = -3x + 4, where the coefficient is -3; and 7x - 6 = 15, where the coefficient is 7. This term introduces the concept of coefficients in linear expressions, forming the foundation for understanding how variables scale in linear equations. |
Variable Expressions |

|
Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term | Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term
TopicLinear Functions DescriptionThe term is "Coefficient of the Linear Term," defined as the numerical factor of the variable in a linear expression, equation, or function. Examples provided include x + 3, where the coefficient is 1; y = -3x + 4, where the coefficient is -3; and 7x - 6 = 15, where the coefficient is 7. This term introduces the concept of coefficients in linear expressions, forming the foundation for understanding how variables scale in linear equations. |
Variable Expressions |

|
Video Definition 34--Linear Function Concepts--Constant Term | Video Definition 34--Linear Function Concepts--Constant Term
TopicLinear Functions DescriptionThe term is "Constant Term," defined as the numerical term of a linear expression, equation, or function. Examples include x + 5, where the constant is 5; y = 5x + 2, where the constant is 2; and 3x - 2y = 10, where the constant is 10. This term explains the role of constants in linear equations, showing how they affect the y-intercept in graphing linear functions. |
Numerical Expressions |

|
Video Definition 34--Linear Function Concepts--Constant Term | Video Definition 34--Linear Function Concepts--Constant Term
TopicLinear Functions DescriptionThe term is "Constant Term," defined as the numerical term of a linear expression, equation, or function. Examples include x + 5, where the constant is 5; y = 5x + 2, where the constant is 2; and 3x - 2y = 10, where the constant is 10. This term explains the role of constants in linear equations, showing how they affect the y-intercept in graphing linear functions. |
Numerical Expressions |

|
Video Definition 34--Linear Function Concepts--Constant Term | Video Definition 34--Linear Function Concepts--Constant Term
TopicLinear Functions DescriptionThe term is "Constant Term," defined as the numerical term of a linear expression, equation, or function. Examples include x + 5, where the constant is 5; y = 5x + 2, where the constant is 2; and 3x - 2y = 10, where the constant is 10. This term explains the role of constants in linear equations, showing how they affect the y-intercept in graphing linear functions. |
Numerical Expressions |

|
Video Definition 34--Linear Function Concepts--Constant Term | Video Definition 34--Linear Function Concepts--Constant Term
TopicLinear Functions DescriptionThe term is "Constant Term," defined as the numerical term of a linear expression, equation, or function. Examples include x + 5, where the constant is 5; y = 5x + 2, where the constant is 2; and 3x - 2y = 10, where the constant is 10. This term explains the role of constants in linear equations, showing how they affect the y-intercept in graphing linear functions. |
Numerical Expressions |

|
Video Definition 34--Linear Function Concepts--Constant Term | Video Definition 34--Linear Function Concepts--Constant Term
TopicLinear Functions DescriptionThe term is "Constant Term," defined as the numerical term of a linear expression, equation, or function. Examples include x + 5, where the constant is 5; y = 5x + 2, where the constant is 2; and 3x - 2y = 10, where the constant is 10. This term explains the role of constants in linear equations, showing how they affect the y-intercept in graphing linear functions. |
Numerical Expressions |

|
Video Definition 34--Linear Function Concepts--Constant Term | Video Definition 34--Linear Function Concepts--Constant Term
TopicLinear Functions DescriptionThe term is "Constant Term," defined as the numerical term of a linear expression, equation, or function. Examples include x + 5, where the constant is 5; y = 5x + 2, where the constant is 2; and 3x - 2y = 10, where the constant is 10. This term explains the role of constants in linear equations, showing how they affect the y-intercept in graphing linear functions. |
Numerical Expressions |
|
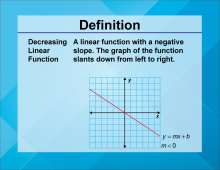
Video Definition 4--Linear Function Concepts--Decreasing Linear Function | Video Definition 4--Linear Function Concepts--Decreasing Linear Function
TopicLinear Functions DescriptionThe term is "Decreasing Linear Function," defined as a linear function with a negative slope. The graph of the function slants down from left to right, represented as y = mx + b with m < 0. This term explores a specific behavior of linear functions, illustrating how slope affects the direction of a graph. |
Slope-Intercept Form |

|
Video Definition 4--Linear Function Concepts--Decreasing Linear Function | Video Definition 4--Linear Function Concepts--Decreasing Linear Function
TopicLinear Functions DescriptionThe term is "Decreasing Linear Function," defined as a linear function with a negative slope. The graph of the function slants down from left to right, represented as y = mx + b with m < 0. This term explores a specific behavior of linear functions, illustrating how slope affects the direction of a graph. |
Slope-Intercept Form |

|
Video Definition 4--Linear Function Concepts--Decreasing Linear Function | Video Definition 4--Linear Function Concepts--Decreasing Linear Function
TopicLinear Functions DescriptionThe term is "Decreasing Linear Function," defined as a linear function with a negative slope. The graph of the function slants down from left to right, represented as y = mx + b with m < 0. This term explores a specific behavior of linear functions, illustrating how slope affects the direction of a graph. |
Slope-Intercept Form |

|
Video Definition 4--Linear Function Concepts--Decreasing Linear Function | Video Definition 4--Linear Function Concepts--Decreasing Linear Function
TopicLinear Functions DescriptionThe term is "Decreasing Linear Function," defined as a linear function with a negative slope. The graph of the function slants down from left to right, represented as y = mx + b with m < 0. This term explores a specific behavior of linear functions, illustrating how slope affects the direction of a graph. |
Slope-Intercept Form |

|
Video Definition 4--Linear Function Concepts--Decreasing Linear Function | Video Definition 4--Linear Function Concepts--Decreasing Linear Function
TopicLinear Functions DescriptionThe term is "Decreasing Linear Function," defined as a linear function with a negative slope. The graph of the function slants down from left to right, represented as y = mx + b with m < 0. This term explores a specific behavior of linear functions, illustrating how slope affects the direction of a graph. |
Slope-Intercept Form |

|
Video Definition 4--Linear Function Concepts--Decreasing Linear Function | Video Definition 4--Linear Function Concepts--Decreasing Linear Function
TopicLinear Functions DescriptionThe term is "Decreasing Linear Function," defined as a linear function with a negative slope. The graph of the function slants down from left to right, represented as y = mx + b with m < 0. This term explores a specific behavior of linear functions, illustrating how slope affects the direction of a graph. |
Slope-Intercept Form |

|
Video Definition 5--Linear Function Concepts--Identity Function | Video Definition 5--Linear Function Concepts--Identity Function
TopicLinear Functions DescriptionThe term is "Identity Function," defined as a linear function of the form y = x, where input values equal the output values. The graph is a line of slope 1. This term explains the simplest linear function and its unique property where the input equals the output. |
Slope-Intercept Form |

|
Video Definition 5--Linear Function Concepts--Identity Function | Video Definition 5--Linear Function Concepts--Identity Function
TopicLinear Functions DescriptionThe term is "Identity Function," defined as a linear function of the form y = x, where input values equal the output values. The graph is a line of slope 1. This term explains the simplest linear function and its unique property where the input equals the output. |
Slope-Intercept Form |

|
Video Definition 5--Linear Function Concepts--Identity Function | Video Definition 5--Linear Function Concepts--Identity Function
TopicLinear Functions DescriptionThe term is "Identity Function," defined as a linear function of the form y = x, where input values equal the output values. The graph is a line of slope 1. This term explains the simplest linear function and its unique property where the input equals the output. |
Slope-Intercept Form |

|
Video Definition 5--Linear Function Concepts--Identity Function | Video Definition 5--Linear Function Concepts--Identity Function
TopicLinear Functions DescriptionThe term is "Identity Function," defined as a linear function of the form y = x, where input values equal the output values. The graph is a line of slope 1. This term explains the simplest linear function and its unique property where the input equals the output. |
Slope-Intercept Form |

|
Video Definition 5--Linear Function Concepts--Identity Function | Video Definition 5--Linear Function Concepts--Identity Function
TopicLinear Functions DescriptionThe term is "Identity Function," defined as a linear function of the form y = x, where input values equal the output values. The graph is a line of slope 1. This term explains the simplest linear function and its unique property where the input equals the output. |
Slope-Intercept Form |

|
Video Definition 5--Linear Function Concepts--Identity Function | Video Definition 5--Linear Function Concepts--Identity Function
TopicLinear Functions DescriptionThe term is "Identity Function," defined as a linear function of the form y = x, where input values equal the output values. The graph is a line of slope 1. This term explains the simplest linear function and its unique property where the input equals the output. |
Slope-Intercept Form |

|
Video Definition 6--Linear Function Concepts--Slope-Intercept Form | Video Definition 6--Linear Function Concepts--Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Slope-Intercept Form," defined as the equation of a linear function written in a form that easily identifies the slope (m) and y-intercept (b). Represented as y = mx + b. This term focuses on the most common representation of linear equations, simplifying analysis and graphing. |
Slope-Intercept Form |

|
Video Definition 6--Linear Function Concepts--Slope-Intercept Form | Video Definition 6--Linear Function Concepts--Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Slope-Intercept Form," defined as the equation of a linear function written in a form that easily identifies the slope (m) and y-intercept (b). Represented as y = mx + b. This term focuses on the most common representation of linear equations, simplifying analysis and graphing. |
Slope-Intercept Form |

|
Video Definition 6--Linear Function Concepts--Slope-Intercept Form | Video Definition 6--Linear Function Concepts--Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Slope-Intercept Form," defined as the equation of a linear function written in a form that easily identifies the slope (m) and y-intercept (b). Represented as y = mx + b. This term focuses on the most common representation of linear equations, simplifying analysis and graphing. |
Slope-Intercept Form |

|
Video Definition 6--Linear Function Concepts--Slope-Intercept Form | Video Definition 6--Linear Function Concepts--Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Slope-Intercept Form," defined as the equation of a linear function written in a form that easily identifies the slope (m) and y-intercept (b). Represented as y = mx + b. This term focuses on the most common representation of linear equations, simplifying analysis and graphing. |
Slope-Intercept Form |

|
Video Definition 6--Linear Function Concepts--Slope-Intercept Form | Video Definition 6--Linear Function Concepts--Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Slope-Intercept Form," defined as the equation of a linear function written in a form that easily identifies the slope (m) and y-intercept (b). Represented as y = mx + b. This term focuses on the most common representation of linear equations, simplifying analysis and graphing. |
Slope-Intercept Form |

|
Video Definition 6--Linear Function Concepts--Slope-Intercept Form | Video Definition 6--Linear Function Concepts--Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Slope-Intercept Form," defined as the equation of a linear function written in a form that easily identifies the slope (m) and y-intercept (b). Represented as y = mx + b. This term focuses on the most common representation of linear equations, simplifying analysis and graphing. |
Slope-Intercept Form |
|
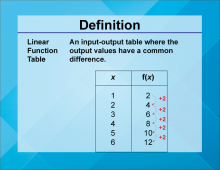
Video Definition 7--Linear Function Concepts--Linear Function Tables | Video Definition 7--Linear Function Concepts--Linear Function Tables
TopicLinear Functions DescriptionThe term is "Linear Function Table," defined as an input-output table where the output values have a common difference. An example shows a table with x-values increasing by 1 and f(x)-values increasing by 2. This term ties numerical patterns to linear functions, highlighting their consistent rate of change. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Definition 7--Linear Function Concepts--Linear Function Tables | Video Definition 7--Linear Function Concepts--Linear Function Tables
TopicLinear Functions DescriptionThe term is "Linear Function Table," defined as an input-output table where the output values have a common difference. An example shows a table with x-values increasing by 1 and f(x)-values increasing by 2. This term ties numerical patterns to linear functions, highlighting their consistent rate of change. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Definition 7--Linear Function Concepts--Linear Function Tables | Video Definition 7--Linear Function Concepts--Linear Function Tables
TopicLinear Functions DescriptionThe term is "Linear Function Table," defined as an input-output table where the output values have a common difference. An example shows a table with x-values increasing by 1 and f(x)-values increasing by 2. This term ties numerical patterns to linear functions, highlighting their consistent rate of change. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Definition 7--Linear Function Concepts--Linear Function Tables | Video Definition 7--Linear Function Concepts--Linear Function Tables
TopicLinear Functions DescriptionThe term is "Linear Function Table," defined as an input-output table where the output values have a common difference. An example shows a table with x-values increasing by 1 and f(x)-values increasing by 2. This term ties numerical patterns to linear functions, highlighting their consistent rate of change. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Definition 7--Linear Function Concepts--Linear Function Tables | Video Definition 7--Linear Function Concepts--Linear Function Tables
TopicLinear Functions DescriptionThe term is "Linear Function Table," defined as an input-output table where the output values have a common difference. An example shows a table with x-values increasing by 1 and f(x)-values increasing by 2. This term ties numerical patterns to linear functions, highlighting their consistent rate of change. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Definition 7--Linear Function Concepts--Linear Function Tables | Video Definition 7--Linear Function Concepts--Linear Function Tables
TopicLinear Functions DescriptionThe term is "Linear Function Table," defined as an input-output table where the output values have a common difference. An example shows a table with x-values increasing by 1 and f(x)-values increasing by 2. This term ties numerical patterns to linear functions, highlighting their consistent rate of change. |
Applications of Linear Functions and Graphs of Linear Functions |
|
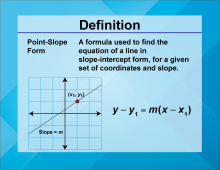
Video Definition 8--Linear Function Concepts--Point-Slope Form | Video Definition 8--Linear Function Concepts--Point-Slope Form
TopicLinear Functions DescriptionThe term is "Point-Slope Form," defined as a formula used to find the equation of a line in slope-intercept form for a given set of coordinates and slope. The formula is y - y1 = m(x - x1). This term provides a useful tool for transitioning between graph-based data and algebraic representations of linear functions. |
Point-Slope Form |