
Illustrative Math Alignment: Grade 8 Unit 3
Linear Equations and Linear Systems
Lesson 14: Solving More Systems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Percents--Equations with Percents: Example 25 | Math Example--Percents--Equations with Percents: Example 25TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "125 is what percent of 2?" The solution involves setting up the equation 2 * (x / 100) = 125, then solving for x to get x = 125 * (100 / 2), which equals 6250%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage well over 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 26 | Math Example--Percents--Equations with Percents: Example 26TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 3.5?" The solution involves setting up the equation 3.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 3.5), which equals 8571.43%. This example introduces a scenario where the resulting percentage is extremely large, over 8000%, due to the first number being significantly larger than the small decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 27 | Math Example--Percents--Equations with Percents: Example 27TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "278 is what percent of 99?" The solution involves setting up the equation 99 * (x / 100) = 278, then solving for x to get x = 278 * (100 / 99), which equals 280.80%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage greater than 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 28 | Math Example--Percents--Equations with Percents: Example 28TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 75.5?" The solution involves setting up the equation 75.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 75.5), which equals 397.35%. This example introduces a scenario where the resulting percentage is close to 400%, with the first number being significantly larger than the decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 29 | Math Example--Percents--Equations with Percents: Example 29TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is what percent of 220?" The solution involves setting up the equation 220 * (x / 100) = 400, then solving for x to get x = 400 * (100 / 220), which equals 181.81%. This example demonstrates how to calculate a percentage when the first number is nearly double the second, resulting in a percentage between 150% and 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 3 | Math Example--Percents--Equations with Percents: Example 3TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 8% of 58?" The solution involves converting 8% to its decimal form, 0.08, and then multiplying it by 58 to arrive at the answer of 4.64. This example introduces a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 30 | Math Example--Percents--Equations with Percents: Example 30TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "333.5 is what percent of 500.25?" The solution involves setting up the equation 500.25 * (x / 100) = 333.5, then solving for x to get x = 333.5 * (100 / 500.25), which is approximately 66.67%. This example introduces a scenario where both numbers are decimals and the resulting percentage is less than 100%, showing how to handle more complex decimal calculations. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 31 | Math Example--Percents--Equations with Percents: Example 31TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "4 is 0.1% of what number?" The solution involves setting up the equation 4 = 0.001 * x, then solving for x to get x = 4 / 0.001, which equals 4000. This example demonstrates how to calculate the whole when given a very small percentage of it, resulting in a much larger number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 32 | Math Example--Percents--Equations with Percents: Example 32TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "7 is 1% of what number?" The solution involves setting up the equation 7 = 0.01 * x, then solving for x to get x = 7 / 0.01, which equals 700. This example introduces a scenario where we need to find the whole when given a small percentage of it, resulting in a number 100 times larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 33 | Math Example--Percents--Equations with Percents: Example 33TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is 30% of what number?" The solution involves setting up the equation 9 = 0.3 * x, then solving for x to get x = 9 / 0.3, which equals 30. This example demonstrates how to calculate the whole when given a larger percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 34 | Math Example--Percents--Equations with Percents: Example 34TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "1 is 400% of what number?" The solution involves setting up the equation 1 = 4.0 * x, then solving for x to get x = 1 / 4, which equals 0.25. This example introduces a scenario where we need to find a number that, when increased by 400%, results in 1, leading to a fraction or decimal less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 35 | Math Example--Percents--Equations with Percents: Example 35TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "15 is 0.25% of what number?" The solution involves setting up the equation 15 = 0.0025 * x, then solving for x to get x = 15 / 0.0025, which equals 6000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 36 | Math Example--Percents--Equations with Percents: Example 36TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "30 is 5% of what number?" The solution involves setting up the equation 30 = 0.05 * x, then solving for x to get x = 30 / 0.05, which equals 600. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a much larger number. |
Solving Percent Equations |
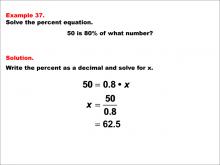
|
Math Example--Percents--Equations with Percents: Example 37 | Math Example--Percents--Equations with Percents: Example 37TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "50 is 80% of what number?" The solution involves setting up the equation 50 = 0.8 * x, then solving for x to get x = 50 / 0.8, which equals 62.5. This example introduces a scenario where we need to find the whole when given a large percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |
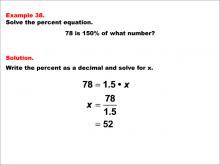
|
Math Example--Percents--Equations with Percents: Example 38 | Math Example--Percents--Equations with Percents: Example 38TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "78 is 150% of what number?" The solution involves setting up the equation 78 = 1.5 * x, then solving for x to get x = 78 / 1.5, which equals 52. This example demonstrates how to calculate the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |
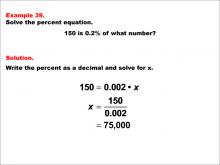
|
Math Example--Percents--Equations with Percents: Example 39 | Math Example--Percents--Equations with Percents: Example 39TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "150 is 0.2% of what number?" The solution involves setting up the equation 150 = 0.002 * x, then solving for x to get x = 150 / 0.002, which equals 75,000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 4 | Math Example--Percents--Equations with Percents: Example 4TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 6.5% of 45.5?" The solution involves converting 6.5% to its decimal equivalent, 0.065, and then multiplying it by 45.5 to obtain the result of 2.9575. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation. |
Solving Percent Equations |
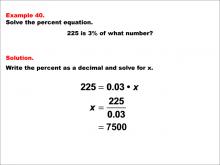
|
Math Example--Percents--Equations with Percents: Example 40 | Math Example--Percents--Equations with Percents: Example 40TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "225 is 3% of what number?" The solution involves setting up the equation 225 = 0.03 * x, then solving for x to get x = 225 / 0.03, which equals 7,500. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 41 | Math Example--Percents--Equations with Percents: Example 41TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is 40% of what number?" The solution involves setting up the equation 400 = 0.4 * x, then solving for x to get x = 400 / 0.4, which equals 1000. This example demonstrates how to calculate the whole when given a significant percentage of it, resulting in a number that is larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 42 | Math Example--Percents--Equations with Percents: Example 42TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "650 is 130% of what number?" The solution involves setting up the equation 650 = 1.3 * x, then solving for x to get x = 650 / 1.3, which equals 500. This example introduces a scenario where we need to find the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 5 | Math Example--Percents--Equations with Percents: Example 5TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 30% of 9?" The solution involves converting 30% to its decimal form, 0.3, and then multiplying it by 9 to get the result of 2.7. This example introduces a larger percentage, demonstrating how the method applies consistently across various percentage values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 6 | Math Example--Percents--Equations with Percents: Example 6TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 28% of 7.2?" The solution involves converting 28% to its decimal equivalent, 0.28, and then multiplying it by 7.2 to obtain the result of 2.016. This example combines a whole number percentage with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 7 | Math Example--Percents--Equations with Percents: Example 7TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 45% of 68?" The solution involves converting 45% to its decimal form, 0.45, and then multiplying it by 68 to arrive at the answer of 30.6. This example introduces a larger percentage and a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 8 | Math Example--Percents--Equations with Percents: Example 8TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 52.3% of 36.9?" The solution involves converting 52.3% to its decimal equivalent, 0.523, and then multiplying it by 36.9 to obtain the result of 19.2987. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation and showcasing the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 9 | Math Example--Percents--Equations with Percents: Example 9TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 150% of 8?" The solution involves converting 150% to its decimal form, 1.5, and then multiplying it by 8 to get the result of 12. This example introduces a percentage greater than 100%, demonstrating how the method applies consistently even when dealing with percentages that represent values larger than the whole. |
Solving Percent Equations |

|
Math Example: Algebra Tiles: Example 1 | Math Example: Algebra Tiles: Example 1TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates the addition of 7 and 12 using algebra tiles. Two groups of yellow tiles, one with 7 tiles and another with 12 tiles, are combined to show a total of 19 tiles. This visual representation helps students understand the concept of addition with positive integers. |
Numerical Expressions |
|
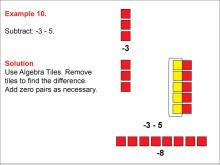
Math Example: Algebra Tiles: Example 10 | Math Example: Algebra Tiles: Example 10TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates the subtraction of 5 from -3 using algebra tiles. The image shows 3 red tiles representing -3, and 5 yellow tiles are added to create zero pairs. After removing the zero pairs, 2 additional red tiles remain, illustrating that -3 - 5 = -8. |
Algebra Tiles--Expressions and Equations |
|
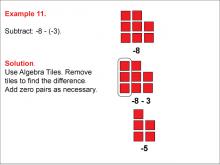
Math Example: Algebra Tiles: Example 11 | Math Example: Algebra Tiles: Example 11TopicNumerical and Algebraic Expressions DescriptionThis example illustrates the subtraction of -3 from -8 using algebra tiles. The image shows 8 red tiles representing -8, and 3 red tiles are removed to demonstrate the subtraction of -3. The result is 5 red tiles, visually showing that -8 - (-3) = -5. |
Algebra Tiles--Expressions and Equations |
|
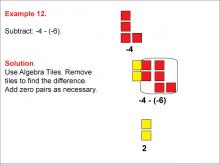
Math Example: Algebra Tiles: Example 12 | Math Example: Algebra Tiles: Example 12TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates the subtraction of -6 from -4 using algebra tiles. The image shows 4 red tiles representing -4, and 6 yellow tiles are added to form zero pairs. After removing these pairs, 2 yellow tiles remain, illustrating that -4 - (-6) = 2. |
Algebra Tiles--Expressions and Equations |

|
Math Example: Algebra Tiles: Example 13 | Math Example: Algebra Tiles: Example 13TopicNumerical and Algebraic Expressions DescriptionThis example illustrates the subtraction of -7 from -7 using algebra tiles. The image shows 7 red tiles representing -7, and 7 red tiles are removed to demonstrate the subtraction of -7. The result is zero tiles remaining, visually showing that -7 - (-7) = 0. |
Algebra Tiles--Expressions and Equations |
|
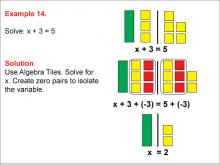
Math Example: Algebra Tiles: Example 14 | Math Example: Algebra Tiles: Example 14TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + 3 = 5 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By creating zero pairs and isolating the variable, the solution x = 2 is visually represented. |
Algebra Tiles--Expressions and Equations |

|
Math Example: Algebra Tiles: Example 15 | Math Example: Algebra Tiles: Example 15TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation x + 4 = 2 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, the solution x = -2 is visually demonstrated. |
Algebra Tiles--Expressions and Equations |
|
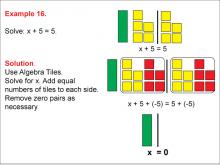
Math Example: Algebra Tiles: Example 16 | Math Example: Algebra Tiles: Example 16TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + 5 = 5 using algebra tiles. The image shows green tiles representing the variable x, and yellow tiles representing positive integers. By manipulating the tiles, students can visually see that x = 0. |
Algebra Tiles--Expressions and Equations |
|
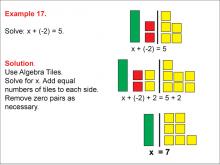
Math Example: Algebra Tiles: Example 17 | Math Example: Algebra Tiles: Example 17TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation x + (-2) = 5 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By strategically moving pieces and creating zero pairs, students can visually determine that x = 7. |
Algebra Tiles--Expressions and Equations |

|
Math Example: Algebra Tiles: Example 18 | Math Example: Algebra Tiles: Example 18TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + 3 = -2 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, students can visually see that x = -5. |
Algebra Tiles--Expressions and Equations |
|
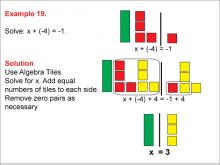
Math Example: Algebra Tiles: Example 19 | Math Example: Algebra Tiles: Example 19TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation x + (-4) = -1 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, students can visually determine that x = 3. |
Algebra Tiles--Expressions and Equations |
|
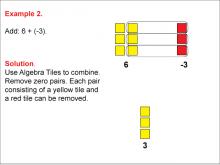
Math Example: Algebra Tiles: Example 2 | Math Example: Algebra Tiles: Example 2TopicNumerical and Algebraic Expressions DescriptionThis example illustrates the addition of 6 and -3 using algebra tiles. It shows 6 yellow tiles representing positive integers and 3 red tiles representing negative integers. After removing zero pairs (one yellow tile cancels out one red tile), the result is 3 yellow tiles, demonstrating that 6 + (-3) = 3. |
Algebra Tiles--Expressions and Equations |
|
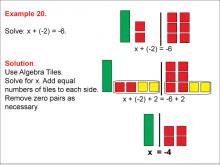
Math Example: Algebra Tiles: Example 20 | Math Example: Algebra Tiles: Example 20TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + (-2) = -6 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, students can visually see that x = -4. |
Algebra Tiles--Expressions and Equations |
|
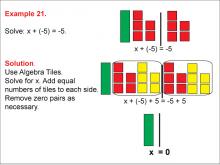
Math Example: Algebra Tiles: Example 21 | Math Example: Algebra Tiles: Example 21TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x+(-5) = -5 using algebra tiles. The image depicts green tiles representing the variable x, red tiles representing negative integers, and yellow tiles representing positive integers. By manipulating these tiles, students can visually see that x = 0. |
Algebra Tiles--Expressions and Equations |
|
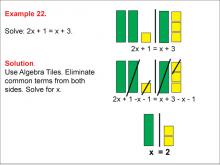
Math Example: Algebra Tiles: Example 22 | Math Example: Algebra Tiles: Example 22
This is part of a collection of math examples that use algebra tiles. This includes modeling integers, sums, differences, and equations. |
Algebra Tiles--Expressions and Equations |
|
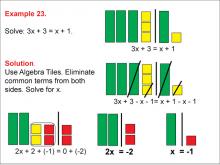
Math Example: Algebra Tiles: Example 23 | Math Example: Algebra Tiles: Example 23TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation 3x + 3 = x + 1 using algebra tiles. The image shows green bars representing the variable x, yellow squares representing positive constants, and red squares representing negative constants. After removing common terms and adding red squares to balance the equation, students can visually see that x = -1. |
Algebra Tiles--Expressions and Equations |
|
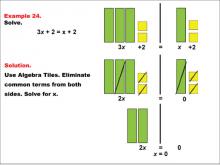
Math Example: Algebra Tiles: Example 24 | Math Example: Algebra Tiles: Example 24TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation 3x + 2 = x + 2 using algebra tiles. The image shows green bars representing the variable x and yellow squares representing constants. After removing common terms from both sides, students can visually see that 2x = 0, leading to the solution x = 0. |
Algebra Tiles--Expressions and Equations |
|
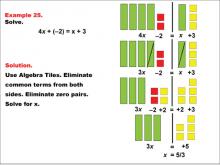
Math Example: Algebra Tiles: Example 25 | Math Example: Algebra Tiles: Example 25TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation 4x + (-2) = x + 3 using algebra tiles. The image shows green bars representing the variable x, yellow squares representing positive constants, and red squares representing negative constants. By eliminating common terms and zero pairs, students can visually determine the solution. |
Algebra Tiles--Expressions and Equations |

|
Math Example: Algebra Tiles: Example 26 | Math Example: Algebra Tiles: Example 26TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation 3x + 4 = x + (-2) using algebra tiles. The image shows green bars representing the variable x, yellow squares representing positive constants, and red squares representing negative constants. By eliminating common terms and zero pairs, students can visually determine the solution. |
Algebra Tiles--Expressions and Equations |
|
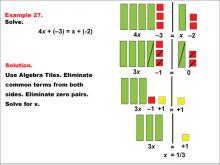
Math Example: Algebra Tiles: Example 27 | Math Example: Algebra Tiles: Example 27TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation 4x + (-3) = x + (-2) using algebra tiles. The image shows green bars representing the variable x, yellow squares representing positive constants, and red squares representing negative constants. By eliminating common terms and zero pairs, students can visually determine the solution. |
Algebra Tiles--Expressions and Equations |
|
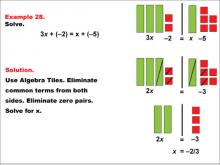
Math Example: Algebra Tiles: Example 28 | Math Example: Algebra Tiles: Example 28TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation 3x + (-2) = x + (-5) using algebra tiles. The image shows green bars representing the variable x, yellow squares representing positive constants, and red squares representing negative constants. By eliminating common terms and zero pairs, students can visually determine that x = -2/3. |
Algebra Tiles--Expressions and Equations |
|
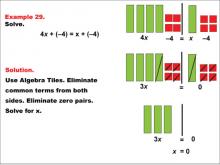
Math Example: Algebra Tiles: Example 29 | Math Example: Algebra Tiles: Example 29TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation 4x + (-4) = x + (-4) using algebra tiles. The image depicts green bars representing the variable x, yellow squares representing positive constants, and red squares representing negative constants. By eliminating common terms and zero pairs, students can visually see that x = 0. |
Algebra Tiles--Expressions and Equations |
|
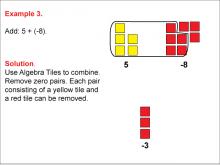
Math Example: Algebra Tiles: Example 3 | Math Example: Algebra Tiles: Example 3TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates the addition of 5 and -8 using algebra tiles. It shows 5 yellow tiles representing positive integers and 8 red tiles representing negative integers. After removing zero pairs, the result is 3 red tiles, illustrating that 5 + (-8) = -3. |
Algebra Tiles--Expressions and Equations |
|
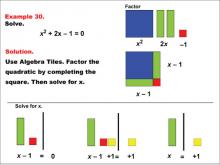
Math Example: Algebra Tiles: Example 30 | Math Example: Algebra Tiles: Example 30TopicNumerical and Algebraic Expressions DescriptionThis example shows a quadratic equation x2 + 2x - 1 = 0 being solved using algebra tiles. The image illustrates factoring by completing the square and solving for x. This visual representation helps students understand the process of solving quadratic equations. |
Algebra Tiles--Expressions and Equations |
|
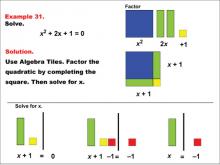
Math Example: Algebra Tiles: Example 31 | Math Example: Algebra Tiles: Example 31TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the quadratic equation x2 + 2x + 1 = 0 using algebra tiles. The image shows factoring as (x + 1)2 = 0 and solving for x, resulting in the solution x = -1. This visual representation helps students understand perfect square trinomials and their solutions. |
Algebra Tiles--Expressions and Equations |