
Illustrative Math Alignment: Grade 8 Unit 3
Linear Equations and Linear Systems
Lesson 14: Solving More Systems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
INSTRUCTIONAL RESOURCE: Tutorial: Solving Two-Step Equations Using the Properties of Equality | INSTRUCTIONAL RESOURCE: Tutorial: Solving Two-Step Equations Using the Properties of Equality
This tutorial goes over the steps of solving a two-step equation by using the properties of equality. Note: The download is a PDF version of this tutorial. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Tutorial: Summary of One-Step Equations | INSTRUCTIONAL RESOURCE: Tutorial: Summary of One-Step Equations
This tutorials provides a summary of the properties of one-step equations. Note: The download is a PDF version of this tutorial. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving One-Step Equations |

|
INSTRUCTIONAL RESOURCE: Tutorial: Visual Models for Equations | INSTRUCTIONAL RESOURCE: Tutorial: Visual Models for Equations
An equation shows a relationship between two quantities. The download is a PDF. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Algebra Tiles--Expressions and Equations and Applications of Equations and Inequalities |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Are Two-Step Equations? | INSTRUCTIONAL RESOURCE: Tutorial: What Are Two-Step Equations?
This tutorial provides an overview of two-step equations. Note: The download is a PDF version of this tutorial. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Is an Equation? | INSTRUCTIONAL RESOURCE: Tutorial: What Is an Equation?
An equation shows a relationship between two quantities. Note: The download is a PDF. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Equations and Inequalities and Variables and Unknowns |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Is a System of Equations? | INSTRUCTIONAL RESOURCE: Tutorial: What Is a System of Equations?
This slide show shows what a system of equations is. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.< Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Systems of Equations |

|
Interactive Crossword Puzzle--Equations 2 | Interactive Crossword Puzzle--Equations 2
Review key vocabulary on the topic of equations with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Applications of Equations and Inequalities, Solving One-Step Equations and Solving Two-Step Equations |

|
Interactive Crossword Puzzle: Equations | Interactive Crossword Puzzle: Equations
Review key vocabulary on the topic of equations with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Applications of Equations and Inequalities |

|
Interactive Math Game: Equation Sort | Description
Use this math game to review true equations, false equations, and conditional equations. The game provides feedback. |
Applications of Equations and Inequalities |

|
Interactive Math Game: Equation Sort 2 | Interactive Math Game: Equation Sort 2
Use this math game to review one-step equations. Students are shown four equations and are asked to correctly label the equation with drag-and-drop. The game provides feedback. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Applications of Equations and Inequalities and Solving One-Step Equations |

|
Interactive Math Game: Equation Sort 3 | Interactive Math Game: Equation Sort 3
Use this math game to review two-step equations. Students are shown four equations and are asked to correctly label the equation with drag-and-drop. The game provides feedback. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Solving Two-Step Equations |

|
Interactive Word Search Puzzle: Equations | Interactive Word Search Puzzle: Equations
Review key vocabulary on the topic of equations with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Applications of Equations and Inequalities |

|
Lesson Plan--Linear Functions and Equations (MS)--Lesson 4--Linear Inequalities | Lesson Plan: Linear InequalitiesThis is the fourth lesson in a five-part series on linear equations and inequalities designed for middle school students. In this lesson, students explore the fundamentals of linear inequalities, including solving inequalities algebraically and graphing solution sets on the coordinate plane. Through step-by-step instruction, students learn to interpret inequality symbols, apply inverse operations, and determine whether to use solid or dashed boundary lines in graphs. The lesson includes real-world applications, such as budgeting constraints, work-hour limits, and spending allowances, demonstrating how linear inequalities are used in everyday decision-making. Aligned with Common Core Standards 6.NS.C.7a, 6.EE.B.5, 8.EE.B.5, and 8.EE.C.7b, this lesson builds on students’ prior knowledge of linear equations while introducing a broader understanding of algebraic inequalities. |
Inequalities |

|
Lesson Plan--Systems of Equations--Lesson 2--Solving by Substitution | Lesson Plan: Solving Systems of Equations by Substitution In this second lesson of the Systems of Equations Unit, students will learn how to solve systems of equations using the substitution method. Substitution is an algebraic technique that allows students to find the solution to a system by replacing one variable with an equivalent expression. Students will: |
Solving Systems of Equations |

|
Lesson Plan--Systems of Equations--Lesson 5--Solving Using Matrices | Lesson Plan Solving Systems Using Matrices In this fifth lesson of the Systems of Equations Unit, students will learn how to solve systems of equations using matrices. Matrices provide an efficient way to organize and manipulate systems of equations, particularly for larger systems. Students will: |
Solving Systems of Equations |
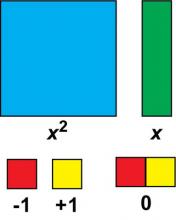
|
Math Clip Art--Algebra Tiles--Algebra Tiles Set | Math Clip Art--Algebra Tiles--Algebra Tiles Set
This is part of a collection of math clip art images that model numbers and expressions using algebra tiles. |
Algebra Tiles--Expressions and Equations |
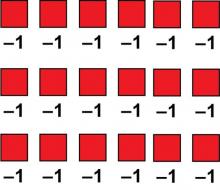
|
Math Clip Art--Algebra Tiles--Negative 1 Algebra Tiles | Math Clip Art--Algebra Tiles--Negative 1 Algebra Tiles
This is part of a collection of math clip art images that model numbers and expressions using algebra tiles. |
Algebra Tiles--Expressions and Equations |

|
Math Clip Art--Algebra Tiles--Positive 1 Algebra Tiles | Math Clip Art--Algebra Tiles--Positive 1 Algebra Tiles
This is part of a collection of math clip art images that model numbers and expressions using algebra tiles. |
Algebra Tiles--Expressions and Equations |
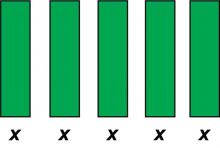
|
Math Clip Art--Algebra Tiles--X Algebra Tiles | Math Clip Art--Algebra Tiles--X Algebra Tiles
This is part of a collection of math clip art images that model numbers and expressions using algebra tiles. |
Algebra Tiles--Expressions and Equations |

|
Math Clip Art--Algebra Tiles--X Squared Algebra Tiles | Math Clip Art--Algebra Tiles--X Squared Algebra Tiles
This is part of a collection of math clip art images that model numbers and expressions using algebra tiles. |
Algebra Tiles--Expressions and Equations |
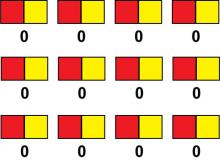
|
Math Clip Art--Algebra Tiles--Zero Pair Algebra Tiles | Math Clip Art--Algebra Tiles--Zero Pair Algebra Tiles
This is part of a collection of math clip art images that model numbers and expressions using algebra tiles. |
Algebra Tiles--Expressions and Equations |
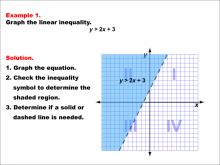
|
Math Example--Inequalities-- Linear Inequalities: Example 1 | Math Example--Inequalities-- Linear Inequalities: Example 1TopicInequalities DescriptionThis example demonstrates how to graph the linear inequality y > 2x + 3. The graph shows a dashed line representing the equation y = 2x + 3, with the region above the line shaded to indicate where the inequality holds true. The use of a dashed line signifies that points on the line itself are not included in the solution set. |
Inequalities |
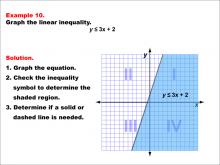
|
Math Example--Inequalities-- Linear Inequalities: Example 10 | Math Example--Inequalities-- Linear Inequalities: Example 10TopicInequalities DescriptionThis example illustrates the graphing of the linear inequality y ≤ 3x + 2. The graph features a solid line representing the equation y = 3x + 2, with the area below the line shaded to indicate the region where the inequality is satisfied. The solid line signifies that points on the line are included in the solution set. |
Inequalities |
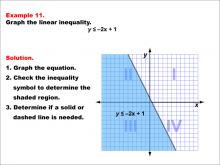
|
Math Example--Inequalities-- Linear Inequalities: Example 11 | Math Example--Inequalities-- Linear Inequalities: Example 11TopicInequalities DescriptionThis example demonstrates the graphing of the linear inequality y ≤ -2x + 1. The graph shows a solid line representing the equation y = -2x + 1, with the region below the line shaded to indicate where the inequality holds true. The solid line signifies that points on the line are included in the solution set. |
Inequalities |
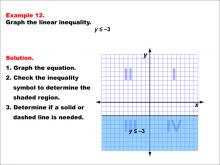
|
Math Example--Inequalities-- Linear Inequalities: Example 12 | Math Example--Inequalities-- Linear Inequalities: Example 12TopicInequalities DescriptionThis example illustrates the graphing of the linear inequality y ≤ -3. The graph features a solid horizontal line at y = -3, with the region below this line shaded to represent the solution set of the inequality. The use of a solid line indicates that points on the line itself are included in the solution. |
Inequalities |
|
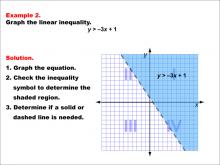
Math Example--Inequalities-- Linear Inequalities: Example 2 | Math Example--Inequalities-- Linear Inequalities: Example 2TopicInequalities DescriptionThis example illustrates the graphing of the linear inequality y > -3x + 1. The graph features a dashed line representing the equation y = -3x + 1, with the area above the line shaded to indicate the region where the inequality is satisfied. The dashed line signifies that points on the line are not part of the solution set. |
Inequalities |
|
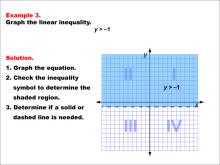
Math Example--Inequalities-- Linear Inequalities: Example 3 | Math Example--Inequalities-- Linear Inequalities: Example 3TopicInequalities DescriptionThis example demonstrates the graphing of the linear inequality y > -1. The graph shows a dashed horizontal line at y = -1, with the region above this line shaded to represent the solution set of the inequality. The use of a dashed line indicates that points on the line itself are not included in the solution. |
Inequalities |
|
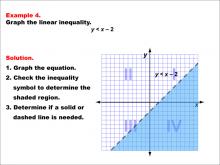
Math Example--Inequalities-- Linear Inequalities: Example 4 | Math Example--Inequalities-- Linear Inequalities: Example 4TopicInequalities DescriptionThis example illustrates the graphing of the linear inequality y < x - 2. The graph features a dashed line representing the equation y = x - 2, with the area below the line shaded to indicate the region where the inequality holds true. The dashed line signifies that points on the line are not included in the solution set. |
Inequalities |
|
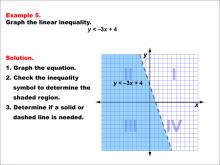
Math Example--Inequalities-- Linear Inequalities: Example 5 | Math Example--Inequalities-- Linear Inequalities: Example 5TopicInequalities DescriptionThis example demonstrates the graphing of the linear inequality y < -3x + 4. The graph shows a dashed line representing the equation y = -3x + 4, with the region below the line shaded to indicate where the inequality holds true. Quadrants II and III are predominantly shaded, illustrating the solution set of this inequality. |
Inequalities |
|
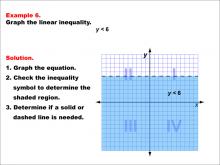
Math Example--Inequalities-- Linear Inequalities: Example 6 | Math Example--Inequalities-- Linear Inequalities: Example 6TopicInequalities DescriptionThis example illustrates the graphing of the linear inequality y < 6. The graph features a horizontal dashed line at y = 6, with the region below this line shaded to represent the solution set of the inequality. Quadrants III and IV are entirely shaded, demonstrating where the inequality holds true. |
Inequalities |
|
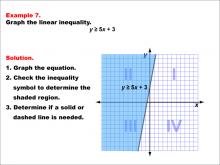
Math Example--Inequalities-- Linear Inequalities: Example 7 | Math Example--Inequalities-- Linear Inequalities: Example 7TopicInequalities DescriptionThis example demonstrates the graphing of the linear inequality y ≥ 5x + 3. The graph shows a solid line representing the equation y = 5x + 3, with the region above the line shaded to indicate where the inequality holds true. Quadrants I and II are predominantly shaded, illustrating the solution set of this inequality. The use of a solid line signifies that points on the line are included in the solution. |
Inequalities |
|
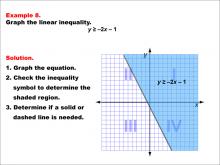
Math Example--Inequalities-- Linear Inequalities: Example 8 | Math Example--Inequalities-- Linear Inequalities: Example 8TopicInequalities DescriptionThis example illustrates the graphing of the linear inequality y ≥ -2x - 1. The graph features a solid line representing the equation y = -2x - 1, with the area above the line shaded to indicate the region where the inequality is satisfied. Quadrants I and IV are predominantly shaded, demonstrating the solution set of this inequality. The solid line signifies that points on the line are included in the solution. |
Inequalities |
|
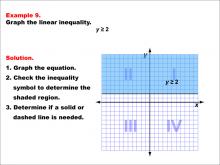
Math Example--Inequalities-- Linear Inequalities: Example 9 | Math Example--Inequalities-- Linear Inequalities: Example 9TopicInequalities DescriptionThis example demonstrates the graphing of the linear inequality y ≥ 2. The graph shows a solid horizontal line at y = 2, with the region above this line shaded to represent the solution set of the inequality. The use of a solid line indicates that points on the line itself are included in the solution. |
Inequalities |

|
Math Example--Percents--Equations with Percents: Example 1 | Math Example--Percents--Equations with Percents: Example 1TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 5% of 8?" The solution involves converting 5% to its decimal form, 0.05, and then multiplying it by 8 to get the result of 0.4. This straightforward approach demonstrates how to tackle basic percent calculations efficiently. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 10 | Math Example--Percents--Equations with Percents: Example 10TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 170% of 9.5?" The solution involves converting 170% to its decimal equivalent, 1.7, and then multiplying it by 9.5 to obtain the result of 16.15. This example combines a percentage greater than 100% with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 11 | Math Example--Percents--Equations with Percents: Example 11TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 225.5% of 78?" The solution involves converting 225.5% to its decimal form, 2.255, and then multiplying it by 78 to arrive at the answer of 175.89. This example introduces a decimal percentage greater than 200% and a larger whole number as the base value, demonstrating the scalability and flexibility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 12 | Math Example--Percents--Equations with Percents: Example 12TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 400% of 92.8?" The solution involves converting 400% to its decimal equivalent, 4.0, and then multiplying it by 92.8 to obtain the result of 371.2. This example showcases how to handle percentages greater than 100% and their application to decimal numbers, illustrating the versatility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 13 | Math Example--Percents--Equations with Percents: Example 13TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "5 is what percent of 9?" The solution involves setting up the equation 9 * (x / 100) = 5, then solving for x to get x = 5 * (100 / 9), which is approximately 55.56%. This example introduces a new type of percent problem where students must find the percentage given two known values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 14 | Math Example--Percents--Equations with Percents: Example 14TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "6 is what percent of 2.3?" The solution involves setting up the equation 2.3 * (x / 100) = 6, then solving for x to get x = 6 * (100 / 2.3), which is approximately 260.87%. This example introduces a scenario where the resulting percentage is greater than 100% and involves a decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 15 | Math Example--Percents--Equations with Percents: Example 15TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is what percent of 38?" The solution involves setting up the equation 38 * (x / 100) = 9, then solving for x to get x = 9 * (100 / 38), which is approximately 23.68%. This example demonstrates how to calculate a percentage when the first number is smaller than the second, resulting in a percentage less than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 16 | Math Example--Percents--Equations with Percents: Example 16TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "2 is what percent of 55.5?" The solution involves setting up the equation 55.5 * (x / 100) = 2, then solving for x to get x = 2 * (100 / 55.5), which is approximately 3.6036%. This example introduces a scenario where the resulting percentage is a small fraction, less than 5%, and involves a decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 17 | Math Example--Percents--Equations with Percents: Example 17TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "8 is what percent of 120?" The solution involves setting up the equation 120 * (x / 100) = 8, then solving for x to get x = 8 * (100 / 120), which is approximately 6.67%. This example demonstrates how to calculate a percentage when dealing with larger whole numbers, resulting in a percentage less than 10%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 18 | Math Example--Percents--Equations with Percents: Example 18TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "3.5 is what percent of 350?" The solution involves setting up the equation 350 * (x / 100) = 3.5, then solving for x to get x = 3.5 * (100 / 350), which equals 1%. This example introduces a scenario where the resulting percentage is a whole number (1%) and involves a decimal number as the first value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 19 | Math Example--Percents--Equations with Percents: Example 19TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "12 is what percent of 8?" The solution involves setting up the equation 8 * (x / 100) = 12, then solving for x to get x = 12 * (100 / 8), which equals 150%. This example demonstrates how to calculate a percentage when the first number is larger than the second, resulting in a percentage greater than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 2 | Math Example--Percents--Equations with Percents: Example 2TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 7% of 9.5?" The solution involves converting 7% to its decimal equivalent, 0.07, and then multiplying it by 9.5 to obtain the result of 0.665. This example builds upon the previous one by introducing a decimal number as the base value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 20 | Math Example--Percents--Equations with Percents: Example 20TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "32 is what percent of 1.5?" The solution involves setting up the equation 1.5 * (x / 100) = 32, then solving for x to get x = 32 * (100 / 1.5), which equals 2133.3%. This example introduces a scenario where the resulting percentage is significantly larger than 100% and involves a decimal base number less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 21 | Math Example--Percents--Equations with Percents: Example 21TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "48 is what percent of 55?" The solution involves setting up the equation 55 * (x / 100) = 48, then solving for x to get x = 48 * (100 / 55), which equals 87.27%. This example demonstrates how to calculate a percentage when the two numbers are relatively close in value, resulting in a percentage close to but less than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 22 | Math Example--Percents--Equations with Percents: Example 22TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "52.2 is what percent of 98.5?" The solution involves setting up the equation 98.5 * (x / 100) = 52.2, then solving for x to get x = 52.2 * (100 / 98.5), which is approximately 52.99%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that is also close to the original numerator. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 23 | Math Example--Percents--Equations with Percents: Example 23TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "68 is what percent of 320?" The solution involves setting up the equation 320 * (x / 100) = 68, then solving for x to get x = 68 * (100 / 320), which equals 21.25%. This example demonstrates how to calculate a percentage when dealing with whole numbers, resulting in a percentage that's less than 25%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 24 | Math Example--Percents--Equations with Percents: Example 24TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "75.5 is what percent of 555.25?" The solution involves setting up the equation 555.25 * (x / 100) = 75.5, then solving for x to get x = 75.5 * (100 / 555.25), which is approximately 13.59%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that's less than 15%. |
Solving Percent Equations |