Illustrative Math Alignment: Grade 8 Unit 3
Linear Equations and Linear Systems
Lesson 9: When Are They the Same?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
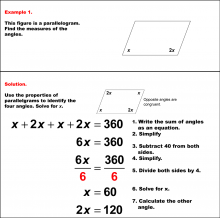
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 1 | Solving Equations with Angle Measures 2--Example 1TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
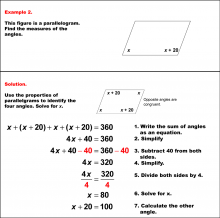
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 10 | Solving Equations with Angle Measures 2--Example 10TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
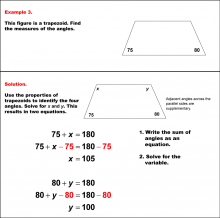
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 2 | Solving Equations with Angle Measures 2--Example 2TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
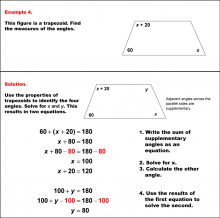
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 3 | Solving Equations with Angle Measures 2--Example 3TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 4 | Solving Equations with Angle Measures 2--Example 4TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
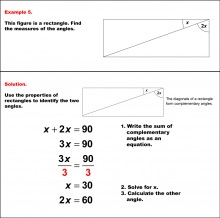
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 5 | Solving Equations with Angle Measures 2--Example 5TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 6 | Solving Equations with Angle Measures 2--Example 6TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 7 | Solving Equations with Angle Measures 2--Example 7TopicEquations DescriptionThis example demonstrates solving equations involving angle measures in a kite. A kite has two pairs of adjacent congruent angles. In this case, we have angles represented as (x+50)°, (x+50)°, (y+20)°, and y°. To solve this problem, we apply two key principles: the sum of angles in a quadrilateral is 360°, and the sum of the angles of a triangle is 180°. You can use the triangle equation to solve for y. Once you determine the value for y, you can use that to find x using either the triangle or the quadrilateral equation. In the solution shown, the triangle equation is used. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
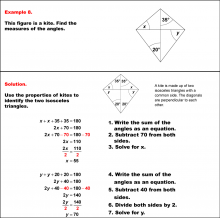
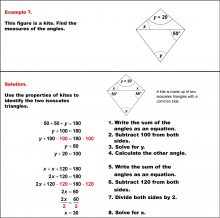
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 8 | Solving Equations with Angle Measures 2--Example 8TopicEquations DescriptionThis example illustrates solving equations involving angle measures in a kite. The kite has two known angles of 70° and 40°, and two unknown angles represented as (x+y)°. To solve this problem, we look at the triangles formed by one of the diagonals of the kite and use the triangle equation. First solve for x with the top triangle. Once you find x, use that value to solve for y in the bottom triangle. You could also use the quadrilateral equation to solve for y. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
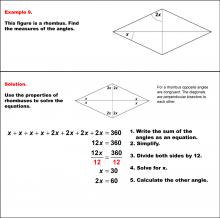
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 9 | Solving Equations with Angle Measures 2--Example 9TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 1 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 1TopicSystems of Equations DescriptionThis image demonstrates solving the system y = 20x + 1 and y = 4x + 1 using elimination. The equations are manipulated by multiplying the second equation by -5 to align coefficients, yielding -5y = -20x - 5. Adding the equations eliminates x, resulting in -4y = -4 or y = 1. Substituting y = 1 into y = 20x + 1 solves x = 0. The intersection point is (0, 1). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 10 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 10TopicSystems of Equations DescriptionThe system y = x + 4 and y = 2x - 5 is solved using elimination. Multiplying the first equation by -2 gives -2y = -2x - 8. Adding cancels x, resulting in -y = -13 or y = 13. Substituting y = 13 into y = x + 4 finds x = 9. The solution is (9, 13). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 2 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 2TopicSystems of Equations DescriptionThis example explains solving y = -12x + 7 and y = -6x + 1 through elimination. The second equation is multiplied by -2, giving -2y = 12x - 2. Adding eliminates x, producing -y = 5 or y = -5. Substituting y = -5 into y = -12x + 7 solves x = 1. The solution is (1, -5). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 3 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 3TopicSystems of Equations DescriptionThis image solves y = 8x - 1 and y = -2x - 1 using elimination. Multiplying the second equation by 4 gives 4y = -8x - 4. Adding eliminates x, leaving 5y = -5 or y = -1. Substituting y = -1 into y = 8x - 1 solves x = 0. The intersection is (0, -1). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 4 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 4TopicSystems of Equations DescriptionThe system y = 2x - 9 and y = -x + 3 is solved via elimination. Doubling the second equation yields 2y = -2x + 6. Adding removes x, leaving 3y = -3 or y = -1. Substituting y = -1 into y = 2x - 9 solves x = 4. The solution is (4, -1). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 5 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 5TopicSystems of Equations DescriptionThis example solves y = 9x + 2 and y = 3x + 2 through elimination. The second equation is multiplied by -3, giving -3y = -9x - 6. Adding eliminates x, yielding -2y = -4 or y = 2. Substituting y = 2 into y = 9x + 2 finds x = 0. The solution is (0, 2). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 6 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 6TopicSystems of Equations DescriptionThis example uses elimination for y = -x - 5 and y = 5x + 7. Multiplying the first equation by 5 produces 5y = -5x - 25. Adding eliminates x, resulting in 6y = -18 or y = -3. Substituting y = -3 into y = -x - 5 finds x = -2. The intersection is (-2, -3). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 7 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 7TopicSystems of Equations DescriptionThis image explains solving y = -x + 9 and y = -2x + 2. Multiplying the first equation by -2 gives -2y = 2x - 18. Adding cancels x, leaving -y = -16 or y = 16. Substituting y = 16 into y = -x + 9 solves x = -7. The intersection is (-7, 16). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 8 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 8TopicSystems of Equations DescriptionThe system y = -6x + 4 and y = -12x - 8 is solved via elimination. Doubling the first equation gives -2y = 12x - 8. Adding eliminates x, resulting in -y = -16 or y = 16. Substituting y = 16 into y = -6x + 4 finds x = -2. The solution is (-2, 16). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 9 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 9TopicSystems of Equations DescriptionThis example solves y = x - 4 and y = 3x + 10 through elimination. Multiplying the first equation by -3 gives -3y = -3x + 12. Adding eliminates x, yielding -2y = 22 or y = -11. Substituting y = -11 into y = x - 4 solves x = -7. The intersection point is (-7, -11). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |
|
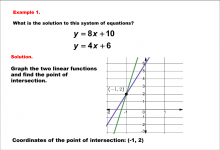
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 1 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 1TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This image solves y = 8x + 10 and y = 4x + 6 graphically. The two linear equations are plotted, and their intersection is visually identified as (-1, 2). The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
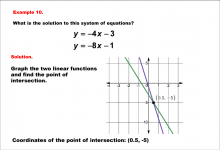
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 10 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 10TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This example graphically solves y = -4x - 3 and y = -8x - 1. The lines intersect at (0.5, -5), which is marked on the graph. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
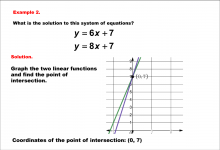
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 2 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 2TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This image demonstrates solving y = 6x + 7 and y = 8x + 7 by graphing. The point of intersection, clearly marked on the graph, is (0, 7). Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
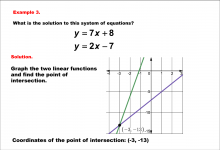
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 3 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 3TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This example illustrates solving y = 7x + 8 and y = 2x - 7 graphically. The intersection point is identified as (-3, -13) by observing where the lines cross. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
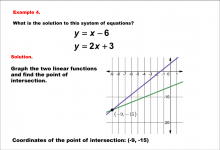
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 4 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 4TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: Graphing y = x - 6 and y = 2x + 3 shows their intersection point at (-9, -15). The graph displays both linear equations and highlights the solution. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
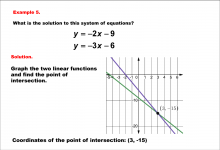
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 5 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 5TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This image uses graphing to solve y = -2x - 9 and y = -3x - 6. The intersection point is identified as (3, -15). Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
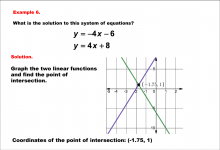
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 6 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 6TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: The system y = -4x - 6 and y = 4x + 8 is solved graphically. The lines intersect at (-1.75, 1), as indicated on the graph. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
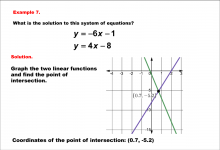
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 7 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 7TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: This example solves y = -6x - 1 and y = 4x - 8 graphically. The intersection point, marked on the graph, is approximately (0.7, -5.2). Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
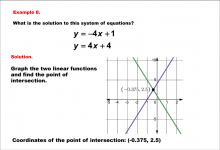
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 8 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 8TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: The equations y = -4x + 1 and y = 4x + 4 are graphed to find the intersection at (-0.375, 2.5). The graph highlights where the two lines meet. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
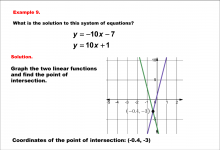
Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 9 | Math Example--Systems of Equations--Solving Linear Systems by Graphing: Example 9TopicSystems of Equations DescriptionThis example solves the system of equations using graphing: Graphing y = -10x - 7 and y = 10x + 1 reveals their intersection point at (-0.4, -3). The graph displays this visually with the crossing of the two lines. Systems of equations involve finding the point of intersection of two or more equations. The graphical method visually demonstrates the solution by plotting the equations on the coordinate plane. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 1 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 1TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: a system of linear equations using substitution. The equations y = -6x + 1 and y = 5x + 1 are solved to find their intersection point. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 10 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 10TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This example solves y = 7x - 10 and y = 5x - 5. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 2 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 2TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: the system of equations y = -x + 3 and y = -3x + 5. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 3 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 3TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: y = 2x + 6 and y = 3x - 2 using substitution. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 4 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 4TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: the equations y = 2x + 9 and y = -3x - 1. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 5 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 5TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: y = -3x + 4 and y = -9x - 8. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 6 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 6TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This example solves y = -9x + 5 and y = -8x + 6. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 7 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 7TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This image solves y = -3x - 9 and y = -2x - 4. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 8 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 8TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: This example calculates the intersection of y = -5x - 9 and y = -6x + 6. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 9 | Math Example--Systems of Equations--Solving Linear Systems by Substitution: Example 9TopicSystems of Equations DescriptionThis example demonstrates solving a system of equations: y = -7x + 2 and y = -6x - 10 are solved. The solution involves finding the point of intersection of the two lines represented by these equations. The graph provides a visual representation, while algebraic techniques validate the intersection point. This dual approach helps in understanding the relationships described by the equations. |
Solving Systems of Equations |
|
Math Example: Solving Linear Systems by Using Matrices: Example 01 | Math Example: Solving Linear Systems by Using Matrices: Example 01TopicSystems of Equations Description
This example solves the system x + y = 5 and x - y = 1 using augmented matrices. The matrix is row-reduced to reveal the solution x = 3 and y = 2. This system demonstrates the method for solving a linear system by the two equations. The variables x and y represent solutions that satisfy both equations simultaneously. Systems of equations are foundational in algebra, offering tools to find points of intersection of lines or solutions to real-world problems involving multiple constraints. These examples provide diverse methods to approach and solve such systems, enriching student comprehension. |
Solving Systems of Equations |
|
Math Example: Solving Linear Systems by Using Matrices: Example 02 | Math Example: Solving Linear Systems by Using Matrices: Example 02TopicSystems of Equations DescriptionThis example addresses the system 2x + y = 7 and x + y = 4 using row reduction. The solution obtained is x = 1 and y = 3. This system demonstrates the method for solving a linear system by the two equations. The variables x and y represent solutions that satisfy both equations simultaneously. Systems of equations are foundational in algebra, offering tools to find points of intersection of lines or solutions to real-world problems involving multiple constraints. These examples provide diverse methods to approach and solve such systems, enriching student comprehension. |
Solving Systems of Equations |
|
Math Example: Solving Linear Systems by Using Matrices: Example 03 | Math Example: Solving Linear Systems by Using Matrices: Example 03TopicSystems of Equations DescriptionThe system 3x - y = 5 and x + y = 3 is solved using augmented matrices. Row reduction yields the solution x = 2 and y = 1. This system demonstrates the method for solving a linear system by - two equations. The variables x and y represent solutions that satisfy both equations simultaneously. Systems of equations are foundational in algebra, offering tools to find points of intersection of lines or solutions to real-world problems involving multiple constraints. These examples provide diverse methods to approach and solve such systems, enriching student comprehension. |
Solving Systems of Equations |
|
Math Example: Solving Linear Systems by Using Matrices: Example 04 | Math Example: Solving Linear Systems by Using Matrices: Example 04TopicSystems of Equations DescriptionThis matrix example solves x + 2y = 8 and x - y = 2 using row reduction. The solution is x = 4 and y = 2. This system demonstrates the method for solving a linear system by solves two equations. The variables x and y represent solutions that satisfy both equations simultaneously. Systems of equations are foundational in algebra, offering tools to find points of intersection of lines or solutions to real-world problems involving multiple constraints. These examples provide diverse methods to approach and solve such systems, enriching student comprehension. |
Solving Systems of Equations |
|
Math Example: Solving Linear Systems by Using Matrices: Example 05 | Math Example: Solving Linear Systems by Using Matrices: Example 05TopicSystems of Equations DescriptionThe system 3x + y = 10 and x - 2y = 1 is solved using row operations on an augmented matrix. The solution is x = 4 and y = 2. This system demonstrates the method for solving a linear system by + two equations. The variables x and y represent solutions that satisfy both equations simultaneously. Systems of equations are foundational in algebra, offering tools to find points of intersection of lines or solutions to real-world problems involving multiple constraints. These examples provide diverse methods to approach and solve such systems, enriching student comprehension. |
Solving Systems of Equations |
|
Math Example: Solving Linear Systems by Using Matrices: Example 06 | Math Example: Solving Linear Systems by Using Matrices: Example 06TopicSystems of Equations DescriptionThis example solves x + 2y = 5 and 3x - y = 1 using the inverse matrix method. The system is converted to matrix form and the inverse matrix is calculated, yielding x = 1 and y = 2. This system demonstrates the method for solving a linear system by x two equations. The variables x and y represent solutions that satisfy both equations simultaneously. |
Solving Systems of Equations |
|
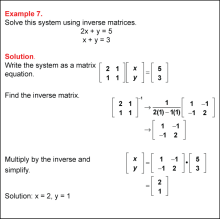
Math Example: Solving Linear Systems by Using Matrices: Example 07 | Math Example: Solving Linear Systems by Using Matrices: Example 07TopicSystems of Equations DescriptionThe system 2x + y = 5 and x + y = 3 is solved using the inverse matrix approach. The solution obtained is x = 2 and y = 1. This system demonstrates the method for solving a linear system by + two equations. The variables x and y represent solutions that satisfy both equations simultaneously. Systems of equations are foundational in algebra, offering tools to find points of intersection of lines or solutions to real-world problems involving multiple constraints. These examples provide diverse methods to approach and solve such systems, enriching student comprehension. |
Solving Systems of Equations |
|
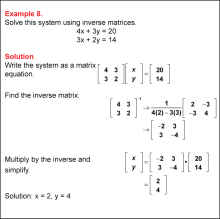
Math Example: Solving Linear Systems by Using Matrices: Example 08 | Math Example: Solving Linear Systems by Using Matrices: Example 08TopicSystems of Equations DescriptionThis matrix example solves 4x + 3y = 20 and 3x + 2y = 14 using inverse matrices. The inverse matrix is computed and applied, yielding x = 2 and y = 4. This system demonstrates the method for solving a linear system by solves two equations. The variables x and y represent solutions that satisfy both equations simultaneously. Systems of equations are foundational in algebra, offering tools to find points of intersection of lines or solutions to real-world problems involving multiple constraints. These examples provide diverse methods to approach and solve such systems, enriching student comprehension. |
Solving Systems of Equations |
|
Math in the News: Issue 6--The BP Oil Spill, a Year Later | Math in the News: Issue 6--The BP Oil Spill, a Year Later
4/25/11. In this issue we discuss the BP oil spill one year after the spill. In particular we look at how damaging oil spills are to marine life and to oxygen levels in the water. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |
|
VIDEO: Overview of Variables and Equations | VIDEO: Overview of Variables and Equations
What Is a Variable?A variable is a symbol, usually a letter, that can stand for different things. |
Variable Expressions, Applications of Equations and Inequalities and Variables and Unknowns |
