
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 22: Volume As a Function of . . .
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
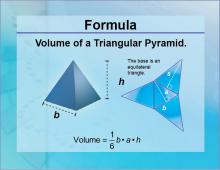
Formulas--Volume of a Triangular Pyramid | Volume of a Triangular Pyramid
Watch this video to learn about the volume of a pyramid. (The video transcript is also included.) Your browser does not support the video tag. Video Transcript Pyramids are majestic and a bit mysterious. Arising from deserts and jungles, they are grand in size and sleek in appearance. Mathematically, pyramids also have an air of mystery. Let’s take a closer look. Here is a cube of side s. Its volume couldn’t be more straightforward: s • s •s, or s-cubed. Its name, its shape, its volume are straightforward. |
Volume |

|
Geometry Applications Teachers Guide: 3D Geometry | Geometry Applications Teachers Guide: 3D Geometry
This is the Teacher's Guide that accompanies Geometry Applications: 3D Geometry. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of 3D Geometry |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 1 | Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 1TopicGeometric Models |
Applications of Surface Area and Volume and Rational Functions and Equations |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2 | Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2TopicGeometric Models |
Surface Area, Volume and Rational Functions and Equations |

|
Google Earth Voyager Story: The Mathematics of Pyramids, Part 1 | Google Earth Voyager Story: The Mathematics of Pyramids, Part 1TopicGeometric Models |
Pyramids |

|
Google Earth Voyager Story: The Mathematics of Pyramids, Part 2 | Google Earth Voyager Story: The Mathematics of Pyramids, Part 2TopicGeometric Models |
Pyramids |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form
This slide show provides 8 examples of quadratic functions in factored form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Standard Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Standard Form
This slide show provides 18 examples of quadratic functions in standard form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Vertex Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Vertex Form
This slide show provides 8 examples of quadratic functions in vertex form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Math Examples 55 | INSTRUCTIONAL RESOURCE: Math Examples--Surface Area
This set of tutorials provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Surface Area |

|
INSTRUCTIONAL RESOURCE: Math Examples 58 | MATH EXAMPLES--Absolute Value Functions in Tabular and Graph Form
This set of tutorials provides 40 examples of absolute value functions in tabular and graph form. NOTE: The download is a PPT file. |
Special Functions |

|
Interactive Math Game--DragNDrop--Evaluating Quadratic Functions | Interactive Math Game--DragNDrop Math--Evaluating Quadratic Functions
In this drag-and-drop game, match f(x) with f(a) for a given value of a. This game generates thousands of different equation combinations, offering an ideal opportunity for skill review in a game format. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Quadratic Equations and Functions |

|
Interactive Math Game--DragNDrop--Linear Functions in Standard Form | Interactive Math Game--DragNDrop Math--Linear Functions in Standard Form
In this drag-and-drop game, match the linear function in standard form with its slope-intercept counterpart. This game generates thousands of different equation combinations, offering an ideal opportunity for skill review in a game format. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Standard Form |

|
Lesson Plan--Linear Functions and Equations (MS)--Lesson 5--Linear Functions and Applications | Lesson Plan: Linear Functions and ApplicationsThis is the fifth and final lesson in a five-part series on linear equations and inequalities designed for middle school students. In this lesson, students explore linear functions in-depth, learning how to represent them using equations, tables, and graphs. They will analyze key function properties, including slope, y-intercept, domain, and range, to develop a complete understanding of how linear functions behave. The lesson focuses on real-world applications, demonstrating how linear functions are used in various fields such as finance, physics, and business. Students will solve problems involving rates of change, cost analysis, and motion, reinforcing the practical significance of linear functions. Through guided practice and hands-on activities, they will interpret linear relationships and predict outcomes using function models. |
Applications of Linear Functions |

|
Lesson Plan: Cross-Sections of 3D Figures, Part 1 | Lesson Plan: Cross-Sections of 3D Figures In this engaging math lesson, students explore cross-sections of cubes, cylinders, and cones through interactive activities, real-world examples, and animated visuals. They will learn how slicing three-dimensional shapes in different ways produces a variety of two-dimensional figures, helping to develop spatial reasoning and geometric understanding. The lesson begins with a conceptual introduction to cross-sections, followed by hands-on practice with everyday objects such as gift boxes, paper towel rolls, and ice cream cones. Students will investigate how horizontal, vertical, and diagonal slices impact the resulting shapes. Animated GIFs illustrate these concepts, reinforcing learning through dynamic visual representations. |
3-Dimensional Figures |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 1 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 1TopicPolynomials DescriptionAn example showing how to find the side lengths of a square given its area, A = x2+ 2x + 1. Example 1: Given the area A = x2+ 2x + 1, find the side lengths. Solution: Express the area as a perfect square, (x + 1)2, so the side lengths are x + 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 2 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 2TopicPolynomials DescriptionAnother example of finding the side lengths of a square with area A = x2+ 4x + 4. Example 2: Given A = x2+ 4x + 4, find the side lengths. Solution: Factor as (x + 2)2, so the side lengths are x + 2. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 3 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 3TopicPolynomials DescriptionShows how to determine the side lengths of a square with area A = x2 - 2x + 1. Example 3: For A = x2 - 2x + 1, the solution expresses it as (x - 1)2, making the side lengths x - 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 4 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 4TopicPolynomials DescriptionExample solving for side lengths of a square with area A = x2 - 4x + 4. Example 4: Given A = x2 - 4x + 4, factor as (x - 2)2 to find side lengths x - 2. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 5 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 5TopicPolynomials DescriptionSolves for side lengths of a square with area A = x2 + 6x + 9. Example 5: With A = x2 + 6x + 9, factor as (x + 3)2, giving side lengths x + 3. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 6 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 6TopicPolynomials DescriptionA cubic example where the volume of a cube, A = x3 + 3x2 + 3x + 1, is used to find the side length. Example 6: Given the volume A = x3 + 3x2 + 3x + 1, factor as (x + 1)3, so the side lengths are x + 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 7 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 7TopicPolynomials DescriptionAnother cubic example solving for side length with volume A = x3 - 3x2 + 3x - 1. Example 7: For the volume A = x3 - 3x2 + 3x - 1, express as (x - 1)3 to determine side lengths of x - 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 1 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 1
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 10 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 10
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 2 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 2
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 3 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 3
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 4 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 4
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 5 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 5
This is part of a collection of math examples that focus on volume. |
Mass and Volume |
|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 6 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 6
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 7 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 7
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 8 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 8
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 9 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 9
This is part of a collection of math examples that focus on volume. |
Mass and Volume |
|
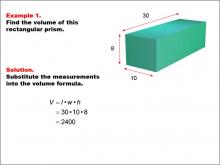
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
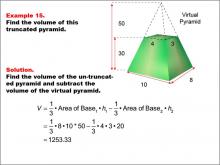
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
|
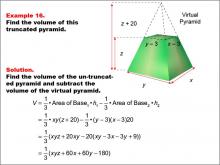
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |
|
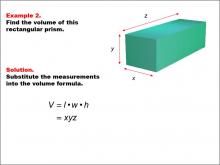
Math Example--Volume Concepts--Calculating Volume: Example 2 | Math Example--Volume Concepts--Calculating Volume: Example 2TopicVolume DescriptionA rectangular prism with dimensions labeled as x, y, and z. The image shows a general example of calculating the volume of a rectangular prism using variables instead of specific numbers. This image illustrates Example 2: The caption describes how to find the volume of a rectangular prism using variables for length (x), width (y), and height (z). The formula is given as V = x * y * z, but no specific values are provided. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 20 | Math Example--Volume Concepts--Calculating Volume: Example 20TopicVolume DescriptionA green cube with side length labeled as x. This image is part of a math example showing how to calculate the volume of a cube using an unknown side length. This image illustrates Example 20: The text explains how to find the volume of a cube with an unknown side length x. The formula used is V = s3, and substituting s = x gives V = x3. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 21 | Math Example--Volume Concepts--Calculating Volume: Example 21TopicVolume DescriptionA hollow cube with an outer edge of 9 and an inner hollow region with an edge of 7. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 21: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 is the outer edge (9) and s2 is the inner edge (7). The solution calculates 9^3 - 7^3 = 386.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 22 | Math Example--Volume Concepts--Calculating Volume: Example 22TopicVolume DescriptionA hollow cube with an outer edge of x and an inner hollow region with an edge of x - 2. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 22: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 = x and s2 = x - 2. Expanding and simplifying gives V = 6x2 - 12x + 8. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 23 | Math Example--Volume Concepts--Calculating Volume: Example 23TopicVolume Description
A cone with a height of 12 and a radius of 4. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 23: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = 4 and h = 12. Substituting these values gives V = (1/3) * π * (42) * 12 = 64π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 24 | Math Example--Volume Concepts--Calculating Volume: Example 24TopicVolume DescriptionA cone with a height labeled as y and a radius labeled as x. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 24: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = x and h = y. Substituting these variables gives V = (x^2 * y)/3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 3 | Math Example--Volume Concepts--Calculating Volume: Example 3TopicVolume DescriptionA hollow rectangular prism with outer dimensions: length = 60, width = 20, and height = 16. The inner hollow part has dimensions: length = 60, width = 18, and height = 14. The image shows how to subtract volumes to find the hollow volume. This image illustrates Example 3: The caption explains how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume. V = (60 * 20 * 16) - (60 * 18 * 14) = 4080. |
Volume |