
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 8: Linear Functions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
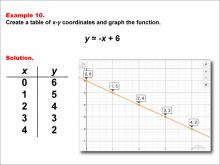
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -x + 6. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 6), (1, 5), (2, 4), (3, 3), and (4, 2), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
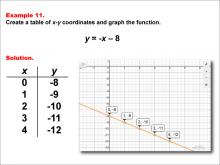
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = -x - 8. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -8), (1, -9), (2, -10), (3, -11), and (4, -12), showing how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
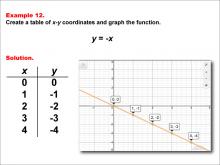
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = -x. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -1), (2, -2), (3, -3), and (4, -4), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
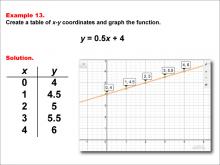
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0.5x + 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 4), (1, 4.5), (2, 5), (3, 5.5), and (4, 6), showing how the y-value increases by 0.5 for each unit increase in x. |
Graphs of Linear Functions |
|
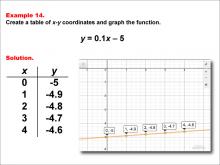
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 14 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 14TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 0.1x - 5. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, -5), (1, -4.9), (2, -4.8), (3, -4.7), and (4, -4.6), illustrating how the y-value increases by 0.1 for each unit increase in x. |
Graphs of Linear Functions |

|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 15 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 15TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0.2x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 0.2), (2, 0.4), (3, 0.6), and (4, 0.8), showing how the y-value increases by 0.2 for each unit increase in x. |
Graphs of Linear Functions |
|
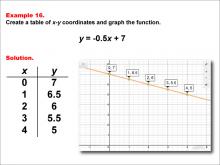
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 16 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 16TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -0.5x + 7. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 7), (1, 6.5), (2, 6), (3, 5.5), and (4, 5), illustrating how the y-value decreases by 0.5 for each unit increase in x. |
Graphs of Linear Functions |
|
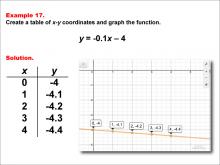
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 17 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 17TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = -0.1x - 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -4), (1, -4.1), (2, -4.2), (3, -4.3), and (4, -4.4), showing how the y-value decreases by 0.1 for each unit increase in x. |
Graphs of Linear Functions |
|
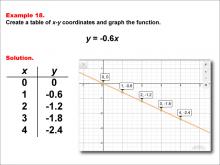
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 18 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 18TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -0.6x. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -0.6), (2, -1.2), (3, -1.8), and (4, -2.4), illustrating how the y-value decreases by 0.6 for each unit increase in x. |
Graphs of Linear Functions |
|
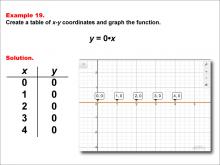
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 19 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 19TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 0), (2, 0), (3, 0), and (4, 0), showing how the y-value remains constant at 0 for all values of x. |
Graphs of Linear Functions |
|
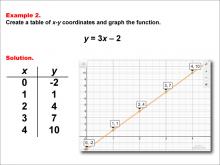
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 2 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 2TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 3x - 2. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -2), (1, 1), (2, 4), (3, 7), and (4, 10), showing how the y-value increases by 3 for each unit increase in x. |
Graphs of Linear Functions |
|
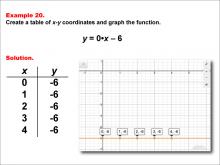
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 20 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 20TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 0x - 6. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, -6), (1, -6), (2, -6), (3, -6), and (4, -6), illustrating how the y-value remains constant at -6 for all values of x. |
Graphs of Linear Functions |
|
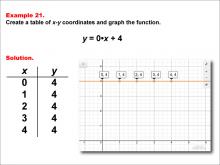
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 21 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 21TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0 * x + 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 4), (1, 4), (2, 4), (3, 4), and (4, 4), showing how the y-value remains constant at 4 for all values of x. |
Graphs of Linear Functions |
|
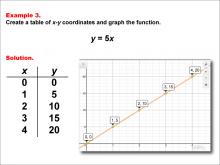
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 3 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 3TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = 5x. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, 5), (2, 10), (3, 15), and (4, 20), illustrating how the y-value increases by 5 for each unit increase in x. |
Graphs of Linear Functions |
|
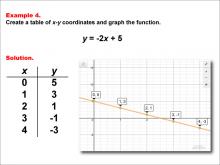
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 4 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 4TopicLinear Functions DescriptionThis example showcases the process of creating a table of x-y coordinates and graphing the linear function y = -2x + 5. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 5), (1, 3), (2, 1), (3, -1), and (4, -3), demonstrating how the y-value decreases by 2 for each unit increase in x. |
Graphs of Linear Functions |
|
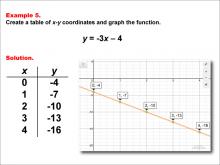
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5TopicLinear Functions DescriptionThis example illustrates the creation of a table of x-y coordinates and the graphing of the linear function y = -3x - 4. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, -4), (1, -7), (2, -10), (3, -13), and (4, -16), showing how the y-value decreases by 3 for each unit increase in x. |
Graphs of Linear Functions |
|
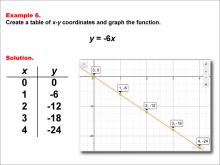
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -6x. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -6), (2, -12), (3, -18), and (4, -24), illustrating how the y-value decreases by 6 for each unit increase in x. |
Graphs of Linear Functions |
|
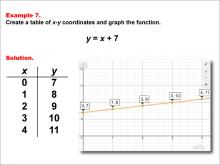
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 7 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 7TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = x + 7. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 7), (1, 8), (2, 9), (3, 10), and (4, 11), showing how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
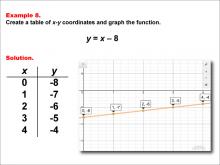
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 8 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 8TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = x - 8. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, -8), (1, -7), (2, -6), (3, -5), and (4, -4), illustrating how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
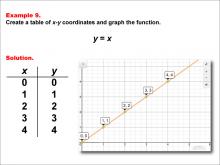
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 9 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 9TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 1), (2, 2), (3, 3), and (4, 4), showing how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |

|
MATH EXAMPLES--Teacher's Guide: Equations of Parallel and Perpendicular Lines | MATH EXAMPLES--Teacher's Guide: Equations of Parallel and Perpendicular Lines
This Teacher's Guide provides an overview of the 32 worked-out examples that show how to find the equation of a line parallel or perpendicular to a given line and through a given point. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Graphs of Linear Functions |

|
MATH EXAMPLES--Teacher's Guide: Finding the Equation of a Line, Given Two Points | MATH EXAMPLES--Teacher's Guide: Finding the Equation of a Line, Given Two Points
This Teacher's Guide provides an overview of the 12 worked-out examples that show how to find the equation of a line, given two points. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Graphs of Linear Functions |

|
MATH EXAMPLES--Teacher's Guide: Graphs of Linear Functions in Slope-Intercept Form | MATH EXAMPLES--Teacher's Guide: Graphs of Linear Functions in Slope-Intercept Form
This Teacher's Guide provides an overview of the 13 worked-out examples that show how to graph a linear function, given the slope and y-intercept. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Graphs of Linear Functions |

|
MATH EXAMPLES--Teacher's Guide: The Point Slope Form | MATH EXAMPLES--Teacher's Guide: The Point Slope Form
This Teacher's Guide provides an overview of the 8 worked-out examples that show how to find the equation of a lineusing the Point Slope Form. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Math in the News: Issue 75--A Swim for the Ages | Math in the News: Issue 75--A Swim for the Ages
August 2013. In this issue we look at Diana Nyad's remarkable swim from Cuba to Florida. It becomes an opportunity to explore Average Speed. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 76--Back to the Moon! | Math in the News: Issue 76--Back to the Moon!
September 2013. In this issue we look at NASA's newest Moon mission, the LADEE robotic probe. It becomes an opportunity to explore linear and logarithmic equations used in rocketry. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Exponential and Logarithmic Functions and Applications of Linear Functions |

|
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Easy) | Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Easy)
This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Point-Slope Form and Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Hard) | Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Hard)
This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Point-Slope Form and Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Medium) | Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Medium)
This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Point-Slope Form and Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Promethean Flipchart: Algebra Applications: Cycling | The relationship between slope and grade in cycling is explored. Go on a tour of Italy through the mountains of Tuscany and apply students' understanding of slope. Note: The download for this resources is the Promethean Flipchart. To access the full video: [Algebra Applications: Linear Functions, Segment 2: Cycling]: https://www.media4math.com/library/video-algebra-applications-linear-functions-segment-2-cycling This video includes a Video Transcript: [Algebra Applications: Linear Functions, Segment 2: Cycling]: https://www.media4math.com/library/video-transcript-algebra-applications-linear-functions-segment-2-cycling |
Applications of Linear Functions |

|
Promethean Flipchart: Algebra Applications: Exercise | Exercise needs to become a consistent part of everyone's lifestyle. In particular, aerobic exercises, which vigorously exerts the heart, is an important form of exercise. The maximum heart rate from aerobic exercise is a linear function dependent on age. Students are asked to develop a data table based on the function. Note: The download for this resources is the Promethean Flipchart. To access the full video: [Algebra Applications: Linear Functions, Segment 4: Exercise]: https://www.media4math.com/library/video-algebra-applications-linear-functions-segment-4-exercise |
Applications of Linear Functions |

|
Promethean Flipchart: Algebra Applications: Oil Drilling | The potential for oil exploration in the controversial Alaska National Wildlife Refuge (ANWR) sets the scene for this problem. A linear regression of oil consumption data over the past 25 years reveals an interesting pattern. How could new oil fields like ANWR help in breaking our dependence on foreign oil? Note: The download for this resources is the Promethean Flipchart. To access the full video [Algebra Applications: Linear Functions, Segment 3: Oil Exploration]: https://www.media4math.com/library/video-algebra-applications-linear-functions-segment-3-oil-exploration |
Applications of Linear Functions |

|
Promethean Flipchart: Algebra Nspirations: Exponential Functions | Almost everyone has an intuitive understanding that exponential growth means rapid growth. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video builds on students’ intuitive notions, explores exponential notation, and analyzes properties of exponential function graphs, with the help of TI-Nspire features such as sliders and graph transformations. Using exponential functions to model finance applications and a Newton’s law of cooling problem further help students build a solid foundation for these fundamental algebraic concepts. Concepts explored: functions, exponents, exponential functions Note: The download for this resources is the Promethean Flipchart. |
Applications of Exponential and Logarithmic Functions |

|
Promethean Flipchart: Algebra Nspirations: Functions and Relations | Functions are relationships between quantities that change. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video explores the definition of a function, its vocabulary and notations, and distinguishes the concept of function from a general relation. Multiple representations of functions are provided using the TI-Nspire, while dynamic visuals and scenarios put them into real-world contexts. Concepts explored: functions, relations, equations, quadratic functions, linear functions, multiple representations Note: The download for this resources is the Promethean Flipchart. This video includes a Video Transcript: https://www.media4math.com/library/video-transcript-algebra-nspirations-functions-and-relations |
Applications of Functions and Relations |

|
Promethean Flipchart: Algebra Nspirations: Linear Functions | In this program, internationally acclaimed mathematics educator Dr. Monica Neagoy, explores the nature of linear functions through the use TI graphing calculators. Examples ranging from air travel, construction, engineering, and space travel provide real-world examples for discovering algebraic concepts. All examples are solved algebraically and then reinforced through the use of the TI-Nspire. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series. Concepts explored: Standard form, slope-intercept form, point-slope form, solving linear equations Note: The download for this resources is the Promethean Flipchart. This video includes a Teacher's Guide: https://www.media4math.com/library/algebra-nspirations-teachers-guide-linear-functions |
Applications of Linear Functions |

|
Promethean Flipchart: Algebra Nspirations: Logarithmic Functions | This video begins with the historical invention of logarithms that forever changed the world of computation—until the advent of calculators more than 300 years later. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, it proceeds to derive the properties of logs, examine logarithmic functions and graphs, and finally explore the well-known Richter logarithmic scale. Concepts explored: functions and inverse functions, logarithms, exponential functions, logarithmic functions Note: The download for this resources is the Promethean Flipchart. To access the full video: [Algebra Nspirations: Logarithms and Logarithmic Functions]: https://www.media4math.com/library/algebra-nspirations-logarithms-and-logarithmic-functions |
Applications of Exponential and Logarithmic Functions |

|
Promethean Flipchart: Algebra Nspirations: Quadratic Functions | In this program, the TI-Nspire is used to explore the nature of quadratic functions. Examples ranging from space travel and projectile motion provide real-world examples for discovering algebraic concepts. All examples are solved graphically. The teacher’s guide provides all keystrokes shown in the video, as well as providing support for TI-84 users. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series. Concepts explored: Quadratic functions and equations, standard form, graphing quadratic equations, solving quadratic equations graphically Note: The download for this resource is the Promethean Flipchart. |
Applications of Quadratic Functions |

|
Promethean Flipchart: Algebra Nspirations: Rational Functions | After briefly reviewing the concept of inverse variation, this video explores Boyle’s law, a real world example of an inversely proportional relationship between pressure and volume of a gas. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, it goes on to examine similarities and differences among rational functions and numbers. Finally, it takes a look at rational functions graphs and ends with a delightful example merging Euclidean and analytic geometry, thanks to the TI-Nspire technology. Concepts explored: functions, rational expressions, rational functions, asymptotes Note: The download for this resources is the Promethean Flipchart. To access the full video [Algebra Nspirations: Rational Functions and Expressions]: https://media4math.com/library/algebra-nspirations-rational-functions-and-expressions |
Rational Functions and Equations |

|
Quizlet Flash Cards: Analyzing Linear Functions | Description In this set of Quizlet flash cards test understanding of linear functions. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Slope-Intercept Form |

|
Quizlet Flash Cards: Composite Functions | Quizlet Flash Cards: Composite FunctionsWhat Are Composite Functions?Modeling Functions |
Composite Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 01 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 02 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 03 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 04 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 05 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 06 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 07 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |