
Illustrative Math Alignment: Grade 8 Unit 8
Pythagorean Theorem and Irrational Numbers
Lesson 8: A Proof of the Pythagorean Theorem
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
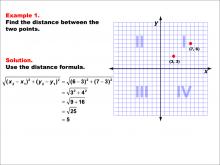
Math Example--Coordinate Geometry--Distance Formula: Example 1 | Math Example--Coordinate Geometry--Distance Formula: Example 1TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (3, 3) and (7, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - 3)2 + (7 - 3)2) = 5. |
The Distance Formula |
|
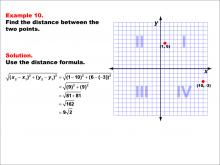
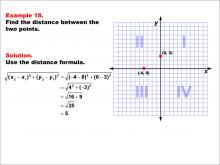
Math Example--Coordinate Geometry--Distance Formula: Example 10 | Math Example--Coordinate Geometry--Distance Formula: Example 10TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (1, 6) and (10, -3) are plotted on a graph, and the distance between them is determined using the formula: √((1 - 10)2 + (6 - (-3))2) = √(9^2 + 9^2) = √162 = 9√2. |
The Distance Formula |
|
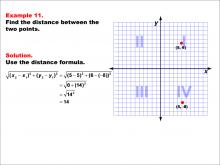
Math Example--Coordinate Geometry--Distance Formula: Example 11 | Math Example--Coordinate Geometry--Distance Formula: Example 11TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (5, 6) and (5, -8) are plotted on a graph, and the distance between them is calculated using the formula: √((5 - 5)2 + (6 - (-8))2) = √(0 + (14)2) = 14. |
The Distance Formula |
|
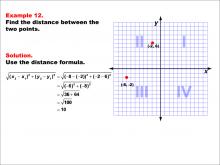
Math Example--Coordinate Geometry--Distance Formula: Example 12 | Math Example--Coordinate Geometry--Distance Formula: Example 12TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-8, -2) and (-2, 6) are plotted on a graph, and the distance between them is determined using the formula: √((-8 - (-2))2 + (-2 - 6)2) = √((-6)2 + (-8)2) = 10. |
The Distance Formula |
|
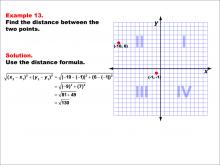
Math Example--Coordinate Geometry--Distance Formula: Example 13 | Math Example--Coordinate Geometry--Distance Formula: Example 13TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-10, 6) and (-1, -1) are plotted on a graph, and the distance between them is calculated using the formula: √((-10 - (-1))2 + (6 - (-1))2) = √((-9)2 + 72) = √130. |
The Distance Formula |
|
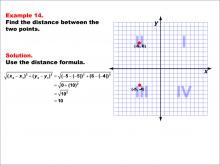
Math Example--Coordinate Geometry--Distance Formula: Example 14 | Math Example--Coordinate Geometry--Distance Formula: Example 14TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (-5, 6) and (-5, -4) are plotted on a graph, and the distance between them is determined using the formula: √((-5 - (-5))2 + (6 - (-4))2) = √(0 + 102) = 10. |
The Distance Formula |
|
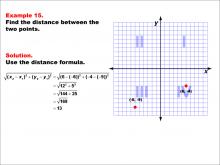
Math Example--Coordinate Geometry--Distance Formula: Example 15 | Math Example--Coordinate Geometry--Distance Formula: Example 15TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-6, -9) and (6, -4) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - (-6))2 + (-4 - (-9))2) = √(122 + 52) = 13. |
The Distance Formula |
|
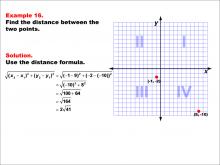
Math Example--Coordinate Geometry--Distance Formula: Example 16 | Math Example--Coordinate Geometry--Distance Formula: Example 16TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-1, -2) and (9, -10) are plotted on a graph, and the distance between them is determined using the formula: √((-1 - 9)2 + (-2 - (-10))2) = √((-10)2 + 82) = 2√41. |
The Distance Formula |
|
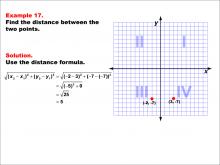
Math Example--Coordinate Geometry--Distance Formula: Example 17 | Math Example--Coordinate Geometry--Distance Formula: Example 17TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the horizontal distance between two points on a coordinate plane. The points (-2, -7) and (3, -7) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 3)2 + (-7 + 7)2) = √((-5)2 + 0) = 5. |
The Distance Formula |
|
Math Example--Coordinate Geometry--Distance Formula: Example 18 | Math Example--Coordinate Geometry--Distance Formula: Example 18TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 0) and (0, 3) are plotted on a graph, and the distance between them is determined using the formula: √((4 - 0)2 + (0 - 3)2) = √(16 + 9) = 5. |
The Distance Formula |
|
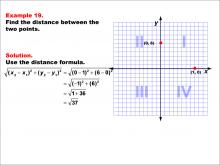
Math Example--Coordinate Geometry--Distance Formula: Example 19 | Math Example--Coordinate Geometry--Distance Formula: Example 19TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (0, 6) and (1, 0) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 1)2 + (6 - 0)2) = √(1 + 36) = √37. |
The Distance Formula |
|
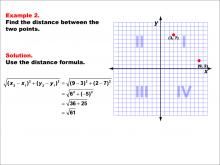
Math Example--Coordinate Geometry--Distance Formula: Example 2 | Math Example--Coordinate Geometry--Distance Formula: Example 2TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (3, 7) and (9, 2) are plotted on a graph, and the distance between them is determined using the formula: √((9 - 3)2 + (2 - 7)2) = √(61). |
The Distance Formula |
|
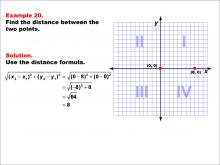
Math Example--Coordinate Geometry--Distance Formula: Example 20 | Math Example--Coordinate Geometry--Distance Formula: Example 20TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the horizontal distance between two points on a coordinate plane. The points (0, 0) and (8, 0) are plotted on a graph, and the distance between them is determined using the formula: √((0 - 8)2 + (0 - 0)2) = √64 = 8. |
The Distance Formula |
|
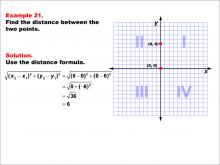
Math Example--Coordinate Geometry--Distance Formula: Example 21 | Math Example--Coordinate Geometry--Distance Formula: Example 21TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (0, 0) and (0, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 0)2 + (0 - 6)2) = √(0 + (-6)2) = 6. |
The Distance Formula |
|
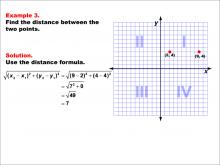
Math Example--Coordinate Geometry--Distance Formula: Example 3 | Math Example--Coordinate Geometry--Distance Formula: Example 3TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (2, 4) and (9, 4) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 2)2 + (4 - 4)2) = 7. |
The Distance Formula |
|
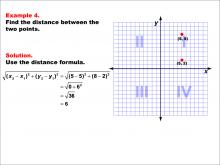
Math Example--Coordinate Geometry--Distance Formula: Example 4 | Math Example--Coordinate Geometry--Distance Formula: Example 4TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (5, 8) and (5, 2) are plotted on a graph, and the distance between them is determined using the formula: √((5 - 5)2 + (8 - 2)2) = 6. |
The Distance Formula |
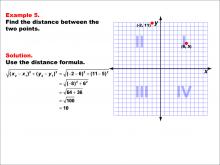
|
Math Example--Coordinate Geometry--Distance Formula: Example 5 | Math Example--Coordinate Geometry--Distance Formula: Example 5TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-2, 11) and (6, 5) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 6)2 + (11 - 5)2) = 10. |
The Distance Formula |
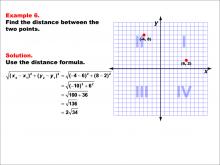
|
Math Example--Coordinate Geometry--Distance Formula: Example 6 | Math Example--Coordinate Geometry--Distance Formula: Example 6TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 8) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-4 - 6)2 + (8 - 2)2) = 2 √(34). |
The Distance Formula |
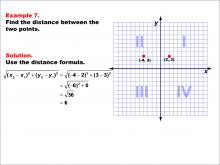
|
Math Example--Coordinate Geometry--Distance Formula: Example 7 | Math Example--Coordinate Geometry--Distance Formula: Example 7TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-4, 3) and (2, 3) are plotted on a graph, and the distance between them is calculated using the formula: √((-4 - 2)2 + (3 - 3)2) = 6. |
The Distance Formula |
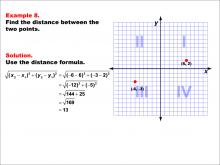
|
Math Example--Coordinate Geometry--Distance Formula: Example 8 | Math Example--Coordinate Geometry--Distance Formula: Example 8TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-6, -3) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-6 - 6)2 + (-3 - 2)2) = 13. |
The Distance Formula |
|
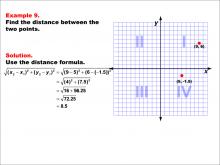
Math Example--Coordinate Geometry--Distance Formula: Example 9 | Math Example--Coordinate Geometry--Distance Formula: Example 9TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (9, 6) and (5, -1.5) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 5)2 + (6 - (-1.5))2) = √(4^2 + 7.5^2) = √72.25 = 8.5. |
The Distance Formula |
|
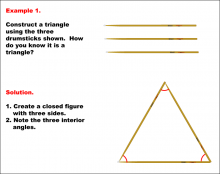
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 1 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 1TopicGeometry DescriptionThis image shows three drumsticks arranged to form a triangle. The drumsticks are placed in a closed triangular shape, with three angles marked in red. This example shows how to construct a triangle using drumsticks. The solution explains that to know it's a triangle, you need to create a closed figure with three sides and note the three interior angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
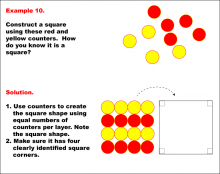
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 10 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 10TopicGeometry DescriptionThe image shows red and yellow circular counters arranged in a grid pattern to form a square shape. The solution explains how to arrange the counters in equal numbers per layer to form a square with four clearly defined corners. This example showcases how to construct a square using these red and yellow counters. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 2 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 2TopicGeometry DescriptionThis image shows a triangle drawn using a crayon. The triangle is closed with three sides, and the three angles are highlighted in red. This example showcases how to draw a triangle using a crayon or pencil. The solution states that to confirm it's a triangle, you need to create a closed figure with three sides and ensure it has three clearly identified angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
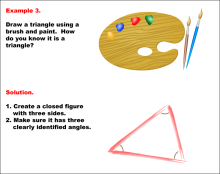
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 3 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 3TopicGeometry DescriptionThis image shows a triangle drawn using paint and a brush. The triangle is closed with three sides, and the three angles are marked in red. This example showcases how to draw a triangle using paint and a brush. The solution explains that to verify it's a triangle, you must create a closed figure with three sides and make sure it has three clearly identified angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 4 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 4TopicGeometry DescriptionThis image shows a triangle formed by arranging stickers in a triangular shape. The stickers form the sides of the triangle, and the angles are highlighted. This example showcases how to draw a triangle using stickers. The solution mentions that you can use stickers to form a closed figure with three sides, ensuring it has three clearly identified angles to confirm it's a triangle. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
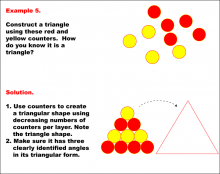
|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 5 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 5TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 6 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 6TopicGeometry DescriptionThe image features four drumsticks arranged in a square shape. The solution highlights how to verify that the figure is a square by checking that it has four sides and four square corners. This example showcases how to construct a square using four drumsticks. The text describes how to create a closed figure with four sides and check for square corners to confirm it's a square. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 7 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 7TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
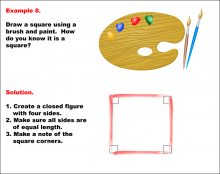
|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 8 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 8TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 9 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 9TopicGeometry DescriptionThe image shows a set of colorful stickers with various holiday-themed designs (hearts, snowmen, reindeer, bells, etc.). The stickers are arranged to form a square shape. The solution demonstrates how to use the stickers to create a square by aligning them in a closed figure with four clear corners. This example showcases how to draw a square using these stickers. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
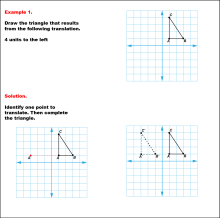
Math Example--Geometric Transformation--Translating Triangles--Example 1 | Math Example--Geometric Transformation--Translating Triangles--Example 1TopicTransformations DescriptionA triangle on a grid is translated 4 units to the left. It shows the original triangle ABC and the translated triangle A'B'C'. Example 1: "Draw the triangle that results from the following translation: 4 units to the left." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
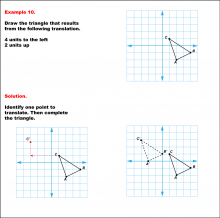
Math Example--Geometric Transformation--Translating Triangles--Example 10 | Math Example--Geometric Transformation--Translating Triangles--Example 10TopicTransformations Description
The triangle is translated 4 units to the left and 2 units up. It displays both the initial and the translated triangles. Example 10: "Draw the triangle that results from the following translation: 4 units to the left, 2 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
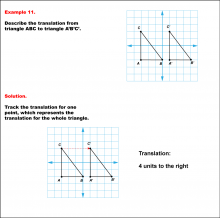
Math Example--Geometric Transformation--Translating Triangles--Example 11 | Math Example--Geometric Transformation--Translating Triangles--Example 11TopicTransformations DescriptionTriangle ABC is translated horizontally to the right by 4 units to form triangle A'B'C'. Example 11: The translation is described as 4 units to the right. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
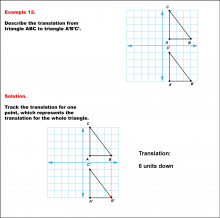
Math Example--Geometric Transformation--Translating Triangles--Example 12 | Math Example--Geometric Transformation--Translating Triangles--Example 12TopicTransformations DescriptionTriangle ABC is translated vertically downward by 6 units to form triangle A'B'C'. Example 12: The translation is described as 6 units down. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
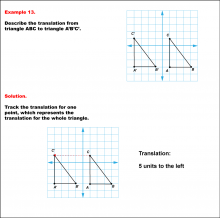
Math Example--Geometric Transformation--Translating Triangles--Example 13 | Math Example--Geometric Transformation--Translating Triangles--Example 13TopicTransformations DescriptionTriangle ABC is translated horizontally to the left by 5 units to form triangle A'B'C'. Example 13: The translation is described as 5 units to the left. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
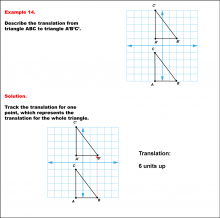
Math Example--Geometric Transformation--Translating Triangles--Example 14 | Math Example--Geometric Transformation--Translating Triangles--Example 14TopicTransformations DescriptionTriangle ABC is translated vertically upward by 6 units to form triangle A'B'C'. Example 14: The translation is described as 6 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
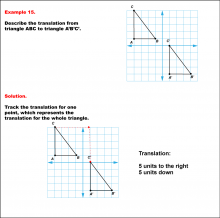
Math Example--Geometric Transformation--Translating Triangles--Example 15 | Math Example--Geometric Transformation--Translating Triangles--Example 15TopicTransformations Description
Triangle ABC is translated diagonally 5 units to the right and 5 units downward to form triangle A'B'C'. Example 15: The translation is described as 5 units to the right and 5 units down. |
Applications of Transformations and Applications of Triangles |
|
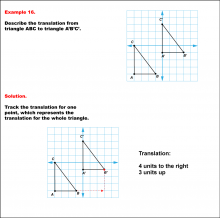
Math Example--Geometric Transformation--Translating Triangles--Example 16 | Math Example--Geometric Transformation--Translating Triangles--Example 16TopicTransformations DescriptionTriangle ABC is translated diagonally 4 units to the right and 3 units upward to form triangle A'B'C'. Example 16: The translation is described as 4 units to the right and 3 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
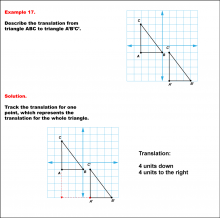
Math Example--Geometric Transformation--Translating Triangles--Example 17 | Math Example--Geometric Transformation--Translating Triangles--Example 17TopicTransformations DescriptionTriangle ABC is translated diagonally 4 units downward and 4 units to the right to form triangle A'B'C'. Example 17: The translation is described as 4 units down and 4 units to the right. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
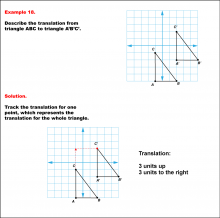
Math Example--Geometric Transformation--Translating Triangles--Example 18 | Math Example--Geometric Transformation--Translating Triangles--Example 18TopicTransformations Description
Triangle ABC is translated diagonally 3 units upward and 3 units to the right to form triangle A'B'C'. Example 18: The translation is described as 3 units up and 3 units to the right. |
Applications of Transformations and Applications of Triangles |
|
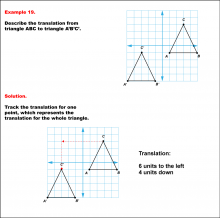
Math Example--Geometric Transformation--Translating Triangles--Example 19 | Math Example--Geometric Transformation--Translating Triangles--Example 19TopicTransformations DescriptionTriangle ABC is translated diagonally 6 units to the left and 4 units downward to form triangle A'B'C'. Example 19: The translation is described as 6 units to the left and 4 units down. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
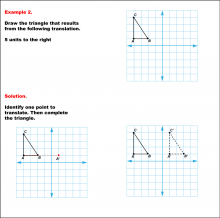
Math Example--Geometric Transformation--Translating Triangles--Example 2 | Math Example--Geometric Transformation--Translating Triangles--Example 2TopicTransformations DescriptionA triangle on a grid is translated 5 units to the right. The diagram shows the original triangle ABC and the new position, A'B'C'.. Example 2: "Draw the triangle that results from the following translation: 5 units to the right." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
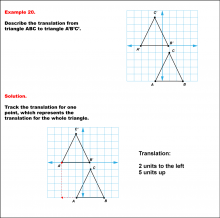
Math Example--Geometric Transformation--Translating Triangles--Example 20 | Math Example--Geometric Transformation--Translating Triangles--Example 20TopicTransformations DescriptionTriangle ABC is translated diagonally 2 units to the left and 5 units upward to form triangle A'B'C'. Example 20: The translation is described as 2 units to the left and 5 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
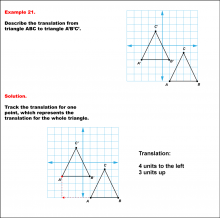
Math Example--Geometric Transformation--Translating Triangles--Example 21 | Math Example--Geometric Transformation--Translating Triangles--Example 21TopicTransformations |
Applications of Transformations and Applications of Triangles |
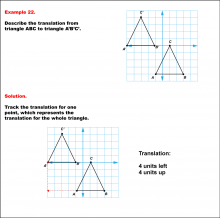
|
Math Example--Geometric Transformation--Translating Triangles--Example 22 | Math Example--Geometric Transformation--Translating Triangles--Example 22TopicTransformations |
Applications of Transformations and Applications of Triangles |
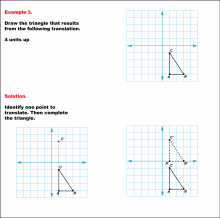
|
Math Example--Geometric Transformation--Translating Triangles--Example 3 | Math Example--Geometric Transformation--Translating Triangles--Example 3TopicTransformations DescriptionA triangle on a grid is translated 4 units up. The figure displays both the original and translated triangles ABC and A'B'C'.. Example 3: "Draw the triangle that results from the following translation: 4 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
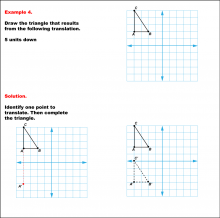
|
Math Example--Geometric Transformation--Translating Triangles--Example 4 | Math Example--Geometric Transformation--Translating Triangles--Example 4TopicTransformations DescriptionA triangle on a grid is translated 5 units down. It shows the original triangle and its new position after translation, labeled A'B'C'. Example 4: "Draw the triangle that results from the following translation: 5 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
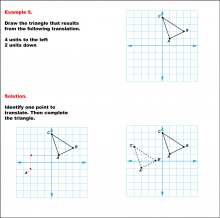
|
Math Example--Geometric Transformation--Translating Triangles--Example 5 | Math Example--Geometric Transformation--Translating Triangles--Example 5TopicTransformations DescriptionA triangle is translated 4 units to the left and 2 units down. Both the original and the new triangles, ABC and A'B'C', are illustrated. Example 5: "Draw the triangle that results from the following translation: 4 units to the left, 2 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
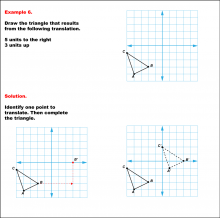
Math Example--Geometric Transformation--Translating Triangles--Example 6 | Math Example--Geometric Transformation--Translating Triangles--Example 6TopicTransformations DescriptionThe triangle is translated 5 units to the right and 3 units up. The image includes both original and translated triangles, labeled ABC and A'B'C'. Example 6: "Draw the triangle that results from the following translation: 5 units to the right, 3 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |