
Illustrative Math Alignment: Grade 7 Unit 3
Measuring Circles
Lesson 8: Relating Area to Circumference
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Video Transcript: Geometry Applications: Circles, Segment 2: Circles and Arcs | Video Transcript: Geometry Applications: Circles, Segment 2: Circles and Arcs
This is the transcript for the video of same title. Video contents: The Roman Coliseum is a large elliptical structure. Yet, the Romans likely used circular arcs to build it. This segment explores the properties of circles and shows how arcs can be used to create elliptical shapes. |
Applications of Circles |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 15TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π. |
Area and Circumference |
|
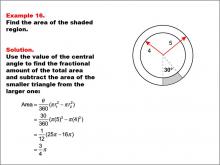
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |
|
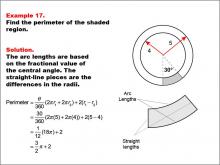
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 17TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 18TopicGeometry DescriptionThis example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2). |
Area and Circumference |
|
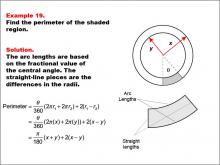
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 19TopicGeometry DescriptionThis example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 20 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 20TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded region in terms of y. The solution involves calculating the difference between the areas of the larger and smaller circles, accounting for the central angle: Area = π/12 * (25 - y2). |
Area and Circumference |
|
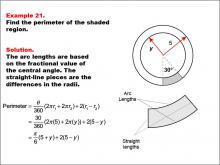
Math Example--Area and Perimeter--Circular Area and Circumference: Example 21 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 21TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. Given a central angle of 30 degrees, radius 5, and unknown radius y, the perimeter is calculated as: Perimeter = π/6 * (5 + y) + 2(5 - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 22 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 22TopicGeometry DescriptionThis example presents two concentric circles with radii 4 and x, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * 42) = (θ * π / 360) * (x2 - 16). |
Area and Circumference |
|
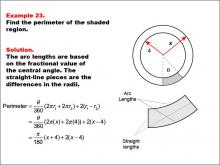
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 23TopicGeometry DescriptionThis example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4). |
Area and Circumference |

|
Video Transcript: Geometry Applications: Circles | Video Transcript: Geometry Applications: Circles
This is the transcript for the video of same title. Video contents: In this program we explore the properties of circles. We do this in the context of two real-world applications. In the first, we look at the design of the Roman Coliseum and explore how circular shapes could have been used to design this elliptical structure. In the second application we look at the Roman Pantheon, specifically its spherical dome, to see how the properties of chords and secants help clarify its unique design. |
Applications of Circles |

|
Video Transcript: Geometry Applications: Circles, Segment 1: The Basics of Circles | Video Transcript: Geometry Applications: Circles, Segment 1: The Basics of Circles
This is the transcript for the video of same title. Video contents: We visit Chaco Canyon in New Mexico to explore the circular kivas and in the process discover how circular buildings have been used to study the heavens. This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Circles |
|
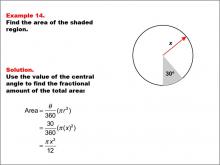
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |

|
Video Transcript: Geometry Applications: Circles, Segment 3: Chords and Inscribed Angles | Video Transcript: Geometry Applications: Circles, Segment 3: Chords and Inscribed Angles
This is the transcript for the video of same title. Video contents: The Roman Pantheon is a domed structure that shows a keen awareness of the position of the sun throughout the year. The source of light from the top of the dome allows for the exploration of chords, inscribed angles, central angles, and intercepted arcs. |
Applications of Circles |

|
Geometry Applications Teachers Guide: Circles | Geometry Applications Teachers Guide: Circles
This is the Teacher's Guide that accompanies Geometry Applications: Circles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Circles |

|
MATH EXAMPLES--Teacher's Guide: Circular Area and Circumference | MATH EXAMPLES--Teacher's Guide: Circular Area and Circumference
This set of tutorials provides 23 examples of solving for the area and circumferences of circles and sections of circles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Area and Circumference |

|
Closed Captioned Video: Geometry Applications: Circles, 3 | Closed Captioned Video: Geometry Applications: Circles, 3TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. The video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 2 | Closed Captioned Video: Geometry Applications: Circles, 2TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Coliseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Coliseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 1 | Closed Captioned Video: Geometry Applications: Circles, 1TopicCircles DescriptionThis segment discusses the geometry of circles and their cultural and astronomical significance. It introduces concepts such as the center, radius, diameter, chords, and arcs, emphasizing their applications in ancient structures like Pueblo Bonito and Stonehenge. Key vocabulary includes equinox, solstice, radius, and chord. Applications include tracking celestial events and designing circular structures for ceremonial or observational purposes. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles | Closed Captioned Video: Geometry Applications: CirclesTopicCircles |
Applications of Circles and Definition of a Circle |

|
Instructional Resource: TI-Nspire Activity: Exploring the Ratio of Circumference to Radius as a Linear Function | In this TI-Nspire Activity, use the Geometry and Graphing Tools to explore the ratio of Circumference to Radius as a linear function. Note: The Preview is a Google Slide Show and the download is a PPT. Subscribers to Media4Math can download resources. To see the complete collection of TI graphing calculator resources, click on this Link. |
Applications of Linear Functions, Applications of Circles and Geometric Constructions with Circles |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter | INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter
In this Algebra Application, students study the direction between diameter and circumference of a circle. Through measurement and data gathering students analyze the line of best fit and explore ways of calculating pi. The math topics covered include: Mathematical modeling, Linear functions, Data gathering and analysis, Ratios, Direct variation. This is a great back-to-school activity for middle school or high school students. This is also a great crossover activity that ties algebra and geometry. |
Applications of Linear Functions, Applications of Ratios, Proportions, and Percents and Applications of Circles |

|
Math in the News: Issue 118--The Return of the Orion | Math in the News: Issue 118 | The Return of the Orion
December 2022. In this issue of Math in the News we look at the Orion rocket's return to Earth from its lunar mission. This provides an opportunity to explore different types of orbits. —PRESS PREVIEW TO SEE THE SLIDE SHOW— This is part of the Math in the News collection. To see the complete collection, click on this link.Note: The download is a PPT file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Circles |

|
SAT Math Lesson Plan 25: Circles and Their Equations | Lesson Plan: SAT Math Lesson 25: Circles and the Coordinate Plane In SAT Math Lesson 25, students explore the geometry of circles using coordinate algebra. This lesson covers:
|
Applications of Circles |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 2 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 2TopicGeometry DescriptionThis example features a circle with a radius of 5 units. The objective is to calculate the circumference of the circle using the given radius. The solution involves applying the circumference formula: C = 2 * π * r = 2 * π * (5) = 10π. Circular area and circumference calculations are fundamental in geometry. These examples provide students with practical applications of theoretical concepts, helping them understand the relationship between a circle's radius and its circumference. |
Area and Circumference |

|
VIDEO: Geometry Applications: Circles, 1 | VIDEO: Geometry Applications: Circles, 1
TopicCircles DescriptionThis segment discusses the geometry of circles and their cultural and astronomical significance. It introduces concepts such as the center, radius, diameter, chords, and arcs, emphasizing their applications in ancient structures like Pueblo Bonito and Stonehenge. Key vocabulary includes equinox, solstice, radius, and chord. Applications include tracking celestial events and designing circular structures for ceremonial or observational purposes. |
Applications of Circles |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
Math in the News: Issue 88--Examining the Polar Vortex | Math in the News: Issue 88--Examining the Polar Vortex
January 2014. In this issue of Math in the News we examine the Polar Vortex. We examine the physics of the cyclonic winds that make up the Polar Vortex and under what conditions the current expansion of Arctic weather affects a large part of the United States. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Circles |

|
Promethean Flipchart: Geometry Applications: Circles 1 | The Roman Coliseum is a large elliptical structure. Yet, the Romans likely used circular arcs to build it. This segment explores the properties of circles and shows how arcs can be used to create elliptical shapes. Note: The download for this resources is the Promethean Flipchart. To access the full video [Geometry Applications: Circles, Segment 2: Circles and Arcs]: https://www.media4math.com/library/geometry-applications-circles-segment-2-circles-and-arcs This video includes a video transcript: https://media4math.com/library/video-transcript-geometry-applications-circles-segment-2-circles-and-arcs |
Applications of Circles |

|
Promethean Flipchart: Geometry Applications: Circles 2 | The Roman Pantheon is a domed structure that shows a keen awareness of the position of the sun throughout the year. The source of light from the top of the dome allows for the exploration of chords, inscribed angles, central angles, and intercepted arcs. Note: The download for this resources is the Promethean Flipchart. To access the full video [Geometry Applications: Circles, Segment 3: Chords and Inscribed Angles]: https://media4math.com/library/geometry-applications-circles-segment-3-chords-and-inscribed-angles This video includes a Video Transcript: https://www.media4math.com/library/video-transcript-geometry-applications-circles-segment-3-chords-and-inscribed-angles |
Applications of Circles |

|
Google Earth Voyager Story: Circular Structures, Part 1 | Google Earth Voyager Story: Circular Structures, Part 1TopicGeometric Models |
Applications of Circles |

|
Google Earth Voyager Story: Circular Structures, Part 2 | Google Earth Voyager Story: Circular Structures, Part 2TopicGeometric Models |
Applications of Circles and Cylinders |
|
Math Clip Art--Venn Diagram 1 | Math Clip Art--Venn Diagram 1
This is part of a collection of math clip art images that show Venn Diagrams. |
Applications of Circles |
|
Math Clip Art--Venn Diagram 2 | Math Clip Art--Venn Diagram 2
This is part of a collection of math clip art images that show Venn Diagrams. |
Applications of Circles |
|
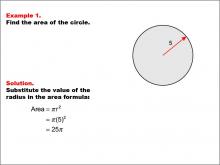
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 1TopicGeometry DescriptionThis example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way. |
Area and Circumference |

|
VIDEO: Geometry Applications: Circles | VIDEO: Geometry Applications: Circles
TopicCircles |
Applications of Circles |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 3TopicGeometry DescriptionThis example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 4TopicGeometry DescriptionThis example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference. |
Area and Circumference |
|
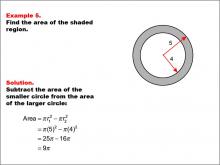
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 5TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes. |
Area and Circumference |
|
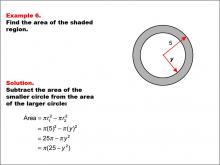
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |
|
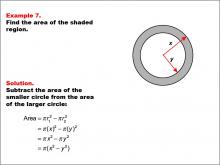
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |
|
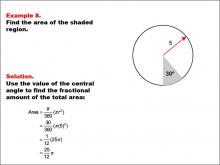
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |
|
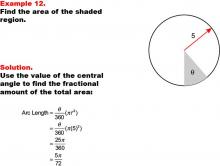
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |