
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 19: Tables, Equations, and Graphs, Oh My!
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
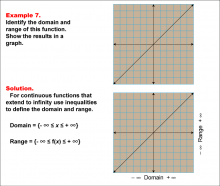
Math Example--Function Concepts--Domain and Range of a Function--Example 7 | Math Example--Function Concepts--Domain and Range of a Function--Example 7TopicArithmetic DescriptionThe example demonstrates find the domain and range for a continuous linear function extending infinitely in both directions. show the results graphically and describe the domain and range. This is illustrated by the accompanying image, which shows since the function extends infinitely, use inequalities to express the domain and range. the domain is -∞ ≤ x ≤ +∞, and the range is -∞ ≤ f(x) ≤ +∞. The graph illustrates a continuous line extending diagonally across the coordinate plane, indicating that both x and f(x) values are unrestricted and can span all real numbers. |
Relations and Functions |
|
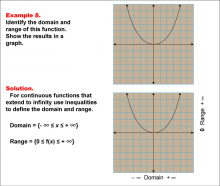
Math Example--Function Concepts--Domain and Range of a Function--Example 8 | Math Example--Function Concepts--Domain and Range of a Function--Example 8TopicArithmetic |
Relations and Functions |
|
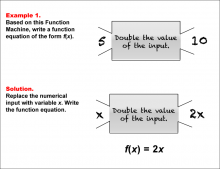
Math Example--Function Concepts--Function Rules and Equations--Example 1 | Math Example--Function Concepts--Function Rules and Equations--Example 1TopicArithmetic DescriptionExample 1: Write a function equation of the form f(x) based on the Function Machine that takes an input and doubles its value. The input shown is 5, and the output is 10. To find the solution, replace the numerical input with the variable x. Since the machine doubles the input, the function equation is f(x) = 2x. |
Relations and Functions |
|
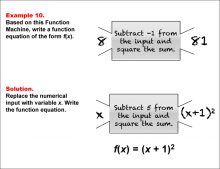
Math Example--Function Concepts--Function Rules and Equations--Example 10 | Math Example--Function Concepts--Function Rules and Equations--Example 10TopicArithmetic DescriptionExample 10: Write a function equation of the form f(x) based on the Function Machine that subtracts -1 (or adds 1) from the input and squares the sum. The input is 8, and the output is 81. Substitute x for the input. The machine subtracts -1 from x (equivalent to adding 1) and squares the result, so the function equation is f(x) = (x + 1)2. |
Relations and Functions |
|
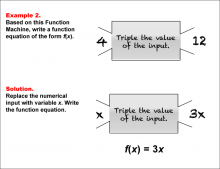
Math Example--Function Concepts--Function Rules and Equations--Example 2 | Math Example--Function Concepts--Function Rules and Equations--Example 2TopicArithmetic DescriptionExample 2: Write a function equation of the form f(x) based on the Function Machine that takes an input and triples its value. The input shown is 4, and the output is 12. By replacing the numerical input with the variable x and applying the machine's rule to triple the input, the function equation is f(x) = 3x. |
Relations and Functions |
|
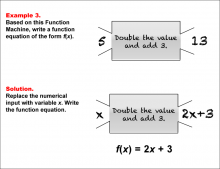
Math Example--Function Concepts--Function Rules and Equations--Example 3 | Math Example--Function Concepts--Function Rules and Equations--Example 3TopicArithmetic DescriptionExample 3: Write a function equation of the form f(x) based on the Function Machine that doubles the value of the input and then adds 3. The input is 5, and the output is 13. To determine the function, replace the input with x. The machine doubles the input and then adds 3, so the function equation is f(x) = 2x + 3. |
Relations and Functions |
|
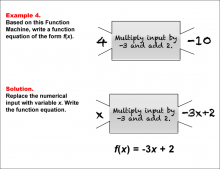
Math Example--Function Concepts--Function Rules and Equations--Example 4 | Math Example--Function Concepts--Function Rules and Equations--Example 4TopicArithmetic DescriptionEΘample 4: Write a function equation of the form f(Θ) based on the Function Machine that multiplies the input by -3 and then adds 2. The input is 4, and the output is -10. Substitute the numerical input with x. Since the machine multiplies the input by -3 and adds 2, the function equation is f(x) = -3x + 2. |
Relations and Functions |
|
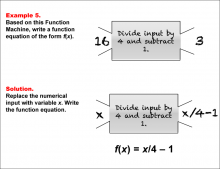
Math Example--Function Concepts--Function Rules and Equations--Example 5 | Math Example--Function Concepts--Function Rules and Equations--Example 5TopicArithmetic DescriptionExample 5: Write a function equation of the form f(x) based on the Function Machine that divides the input by 4 and then subtracts 1. The input shown is 16, and the output is 3. Replace the input with x. Applying the function machine's rule to divide by 4 and subtract 1, the function equation is f(x) = x / 4 - 1. |
Relations and Functions |
|
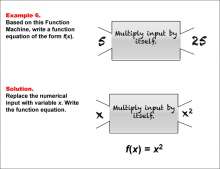
Math Example--Function Concepts--Function Rules and Equations--Example 6 | Math Example--Function Concepts--Function Rules and Equations--Example 6TopicArithmetic DescriptionExample 6: Write a function equation of the form f(x) based on the Function Machine that multiplies the input by itself (squares it). The input is 5, and the output is 25. Substitute the input with x. Since the machine squares the input, the function equation is f(x) = x2. |
Relations and Functions |
|
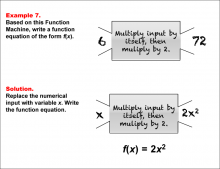
Math Example--Function Concepts--Function Rules and Equations--Example 7 | Math Example--Function Concepts--Function Rules and Equations--Example 7TopicArithmetic DescriptionExample 7: Write a function equation of the form f(x) based on the Function Machine that multiplies the input by itself and then multiplies the result by 2. The input is 6, and the output is 72. Replace the input with x. The machine squares the input and then multiplies it by 2, so the function equation is f(x) = 2x2. |
Relations and Functions |
|
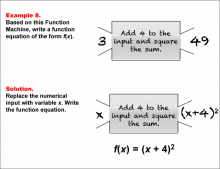
Math Example--Function Concepts--Function Rules and Equations--Example 8 | Math Example--Function Concepts--Function Rules and Equations--Example 8TopicArithmetic DescriptionExample 8: Write a function equation of the form f(x) based on the Function Machine that adds 4 to the input and then squares the sum. The input is 3, and the output is 49. Substitute x for the input. The machine adds 4 to x and then squares the result, giving the function equation f(x) = (x + 4)2. |
Relations and Functions |
|
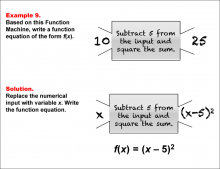
Math Example--Function Concepts--Function Rules and Equations--Example 9 | Math Example--Function Concepts--Function Rules and Equations--Example 9TopicArithmetic DescriptionExample 9: Write a function equation of the form f(x) based on the Function Machine that subtracts 5 from the input and then squares the sum. The input is 10, and the output is 25. Replace the input with x. Since the machine subtracts 5 from x and squares the result, the function equation is f(x) = (x - 5)2. |
Relations and Functions |
|
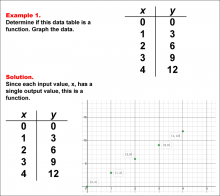
Math Example--Function Concepts--Function Tables--Example 1 | Math Example--Function Concepts--Function Tables--Example 1
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |

|
Math Example--Function Concepts--Function Tables--Example 10 | Math Example--Function Concepts--Function Tables--Example 10
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
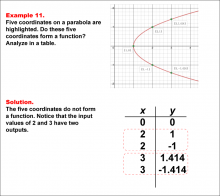
Math Example--Function Concepts--Function Tables--Example 11 | Math Example--Function Concepts--Function Tables--Example 11
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |

|
Math Example--Function Concepts--Function Tables--Example 12 | Math Example--Function Concepts--Function Tables--Example 12
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
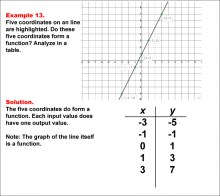
Math Example--Function Concepts--Function Tables--Example 13 | Math Example--Function Concepts--Function Tables--Example 13
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
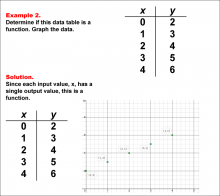
Math Example--Function Concepts--Function Tables--Example 2 | Math Example--Function Concepts--Function Tables--Example 2
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
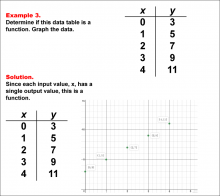
Math Example--Function Concepts--Function Tables--Example 3 | Math Example--Function Concepts--Function Tables--Example 3
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
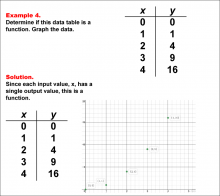
Math Example--Function Concepts--Function Tables--Example 4 | Math Example--Function Concepts--Function Tables--Example 4
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
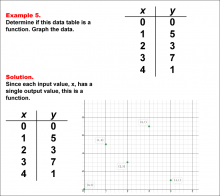
Math Example--Function Concepts--Function Tables--Example 5 | Math Example--Function Concepts--Function Tables--Example 5
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
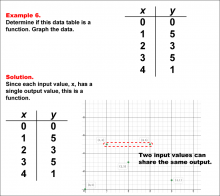
Math Example--Function Concepts--Function Tables--Example 6 | Math Example--Function Concepts--Function Tables--Example 6
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
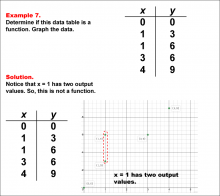
Math Example--Function Concepts--Function Tables--Example 7 | Math Example--Function Concepts--Function Tables--Example 7
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
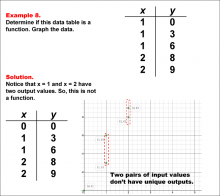
Math Example--Function Concepts--Function Tables--Example 8 | Math Example--Function Concepts--Function Tables--Example 8
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
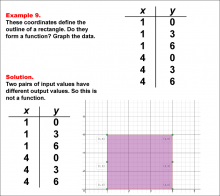
Math Example--Function Concepts--Function Tables--Example 9 | Math Example--Function Concepts--Function Tables--Example 9
This is part of a collection of math examples that focus on function concepts. |
Relations and Functions |
|
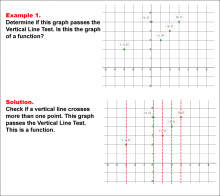
Math Example--Function Concepts--Vertical Line Test--Example 1 | Math Example--Function Concepts--Vertical Line Test--Example 1TopicArithmetic DescriptionThis example illustrates a scatter plot with several points labeled with their coordinates. The task is to determine whether the graph passes the vertical line test to qualify as a function. The solution demonstrates that no vertical line intersects the graph at more than one point, confirming that it is a function. |
Relations and Functions |
|
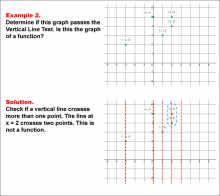
Math Example--Function Concepts--Vertical Line Test--Example 2 | Math Example--Function Concepts--Vertical Line Test--Example 2TopicArithmetic DescriptionThis example illustrates a scatter plot where one vertical line intersects the graph at two points, indicating that the graph fails the vertical line test. The solution clearly identifies this violation and concludes that the graph is not a function. |
Relations and Functions |
|
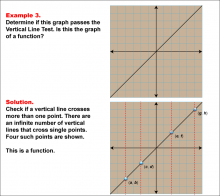
Math Example--Function Concepts--Vertical Line Test--Example 3 | Math Example--Function Concepts--Vertical Line Test--Example 3TopicArithmetic DescriptionThis example illustrates a continuous linear graph passing through several labeled points. the task is to verify the vertical line test. The solution shows that every vertical line crosses the graph at exactly one point, confirming it as a function. |
Relations and Functions |
|
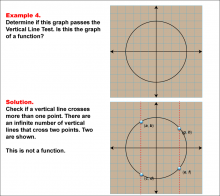
Math Example--Function Concepts--Vertical Line Test--Example 4 | Math Example--Function Concepts--Vertical Line Test--Example 4TopicArithmetic DescriptionThis example illustrates a circular graph and tests its compliance with the vertical line test. the solution shows that some vertical lines intersect the graph at two points, proving that it fails the test and is not a function. |
Relations and Functions |
|
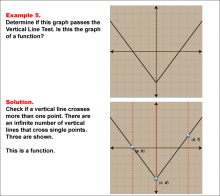
Math Example--Function Concepts--Vertical Line Test--Example 5 | Math Example--Function Concepts--Vertical Line Test--Example 5TopicArithmetic DescriptionThis example illustrates a v-shaped graph. The task is to check its validity as a function using the vertical line test. The solution illustrates that all vertical lines cross the graph at only one point, verifying that it is a function. |
Relations and Functions |
|
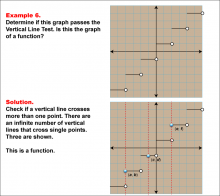
Math Example--Function Concepts--Vertical Line Test--Example 6 | Math Example--Function Concepts--Vertical Line Test--Example 6TopicArithmetic DescriptionThis example illustrates a stepwise graph where the task is to apply the vertical line test. The solution confirms that no vertical line crosses the graph at more than one point, confirming that it is a function. The Vertical Line Test is an essential concept in determining whether a graph represents a function. By drawing vertical lines across the graph, one can assess if any vertical line intersects the graph more than once, indicating it is not a function. The examples in this collection provide a visual and interactive way for students to comprehend this concept. |
Relations and Functions |

|
Quizlet Flash Cards: Evaluating Functions | Description In this set of Quizlet flash cards test understanding of functions. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Relations and Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 01 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 02 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 03 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 04 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 05 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 06 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 07 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 08 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 09 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 10 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Identifying Functions | Description In this set of Quizlet flash cards test understanding of functions. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Relations and Functions |

|
SAT Math Lesson Plan 19: Functions and Their Properties | SAT Math Lesson Plan 19: Functions and Their Properties This comprehensive SAT Math lesson on Functions and Their Properties covers the key concepts necessary to master this topic on the SAT exam. Students will explore function notation, transformations of functions, identifying the domain and range of a function, and understanding the behavior of functions. The lesson is designed to help students develop strong problem-solving skills, providing step-by-step guidance on how to evaluate functions and analyze their transformations. With 45 minutes of focused instruction, this lesson includes engaging examples and practice problems that directly align with the SAT Math exam. |
Relations and Functions |

|
Video Transcript: Algebra Applications: Functions and Relations | Video Transcript: Algebra Applications: Functions and Relations
This is the transcript for the video of same title. Video contents: In this episode of Algebra Applications, students explore the following scenario: Scientists use conic sections to map the trajectories of spacecraft in flight. The setting for this episode is a planned future flight to Mars. As the ship travels from Earth to Mars, parabolic, circular, and elliptical paths are explored. In the process students will learn the difference between a quadratic relation and a quadratic function. |
Applications of Functions and Relations and Relations and Functions |

|
Video Transcript: Algebra Applications: Functions and Relations, Segment 1: Introduction | Video Transcript: Algebra Applications: Functions and Relations, Segment 1: Introduction
This is the transcript for the video of same title. Video contents: Scientists use conic sections to map the trajectories of spacecraft in flight. The setting for this episode is a planned future flight to Mars. As the ship travels from Earth to Mars, parabolic, circular, and elliptical paths are explored. In the process students will learn the difference between a quadratic relation and a quadratic function. |
Applications of Functions and Relations and Relations and Functions |

|
Video Transcript: Algebra Applications: Functions and Relations, Segment 2: Parabolic Paths. | Video Transcript: Algebra Applications: Functions and Relations, Segment 2: Parabolic Paths.
This is the transcript for the video of same title. Video contents: The liftoff and pre-orbital path of the rock is described by a parabola. Students explore the properties of parabolas from the standpoint of the parametric equations that describe the horizontal and vertical directions of motion for the rocket. |
Applications of Functions and Relations and Relations and Functions |

|
Video Transcript: Algebra Applications: Functions and Relations, Segment 3: Circular Paths | Video Transcript: Algebra Applications: Functions and Relations, Segment 3: Circular Paths
This is the transcript for the video of same title. Video contents: The path of a rocket orbiting the Earth can be modeled with the equation of a circle. Students explore the quadratic relation and the parametric equations that can be used to model the path of a spacecraft orbiting Earth. |
Applications of Functions and Relations and Relations and Functions |

|
Video Transcript: Algebra Applications: Functions and Relations, Segment 4: Elliptical Paths | Video Transcript: Algebra Applications: Functions and Relations, Segment 4: Elliptical Paths
This is the transcript for the video of same title. Video contents: The planets orbiting the sun follow elliptical paths. In fact, the trajectory of a spacecraft traveling to Mars would also be elliptical. Students explore these various ellipses. This is part of a collection of video transcript from the Algebra Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Functions and Relations and Relations and Functions |

|
Video Transcript: Algebra Nspirations: Functions and Relations | Video Transcript: Algebra Nspirations: Functions and Relations
This is the transcript for the video of same title. Video contents: Functions are relationships between quantities that change. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video explores the definition of a function, its vocabulary and notations, and distinguishes the concept of function from a general relation. Multiple representations of functions are provided using the TI-Nspire, while dynamic visuals and scenarios put them into real-world contexts. Concepts explored: functions, relations, equations, quadratic functions, linear functions, multiple representations |
Applications of Functions and Relations and Relations and Functions |