
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 19: Tables, Equations, and Graphs, Oh My!
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
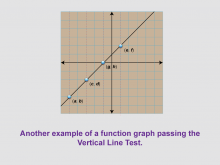
Math Clip Art--Function Concepts--Function Graphs 07 | Math Clip Art--Function Concepts--Function Graphs 07TopicFunctions DescriptionThis image shows a graph with a diagonal line passing through several points on a grid. Red dashed vertical lines indicate that the line passes the vertical line test, providing another example of a function graph that satisfies this crucial criterion. |
Relations and Functions |
|
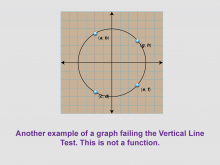
Math Clip Art--Function Concepts--Function Graphs 08 | Math Clip Art--Function Concepts--Function Graphs 08TopicFunctions DescriptionThis image illustrates a circular graph with points plotted on a grid. Red dashed vertical lines are drawn through the circle, clearly demonstrating that it fails the vertical line test by intersecting multiple points vertically. This visual representation serves as an excellent example of a graph that does not represent a function. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Graphs 09 | Math Clip Art--Function Concepts--Function Graphs 09TopicFunctions DescriptionThis image serves as an end card that can be used in conjunction with other images focusing on the vertical line test. It provides a concise summary of the key concept: The Vertical Line Test. This visual aid is designed to reinforce the importance of this test in determining whether a graph represents a function. |
Relations and Functions |

|
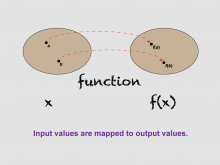
Math Clip Art--Function Concepts--Function Representations 01 | Math Clip Art--Function Concepts--Function Representations 01TopicFunctions DescriptionThis image serves as a title card for a series of 21 images focused on function representations. It sets the stage for exploring various ways to visualize and understand functions, emphasizing the concept of mapping inputs to outputs. Using this image, educators can introduce students to the concept of function representations. It provides a starting point for discussions on how functions can be visualized in different formats, such as diagrams, tables, and graphs. |
Relations and Functions |
|
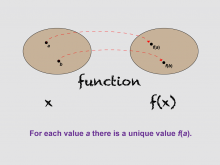
Math Clip Art--Function Concepts--Function Representations 02 | Math Clip Art--Function Concepts--Function Representations 02TopicFunctions DescriptionThis diagram illustrates a function mapping where inputs 'a' and 'b' are associated with outputs f(a) and f(b). It visually represents the fundamental idea that each input has a unique output, emphasizing the one-to-one correspondence in functions. This image can be used by educators to teach students about basic function concepts. By showing how inputs are uniquely mapped to outputs, it reinforces the definition of a function and helps students visualize these relationships. |
Relations and Functions |
|
Math Clip Art--Function Concepts--Function Representations 03 | Math Clip Art--Function Concepts--Function Representations 03TopicFunctions DescriptionThis image presents a function diagram where each input 'a' has a unique output f(a). It underscores the principle that every input corresponds to exactly one output, which is central to understanding functions. This visual can be used by teachers to help students comprehend the concept of unique mappings in functions. It serves as an effective tool for illustrating how each input value is paired with one specific output value. |
Relations and Functions |
|
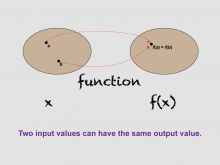
Math Clip Art--Function Concepts--Function Representations 04 | Math Clip Art--Function Concepts--Function Representations 04TopicFunctions DescriptionThis diagram demonstrates how two different inputs 'a' and 'b' can map to the same output f(a)=f(b). It highlights an important aspect of functions where multiple inputs may share an identical output value. This image can be used by educators to explain scenarios where different inputs lead to the same result within functions. It helps students understand that while each input has one output, multiple inputs can share that output. |
Relations and Functions |
|
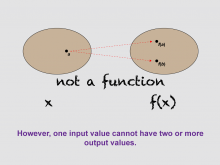
Math Clip Art--Function Concepts--Function Representations 05 | Math Clip Art--Function Concepts--Function Representations 05TopicFunctions DescriptionThis diagram shows an input 'a' mapping to two outputs f(a) and f(b), labeled "not a function." It illustrates that in valid functions, an input cannot correspond to multiple outputs. This image helps educators explain why certain mappings do not qualify as functions. By showing an invalid example, it reinforces the rule that each input must have only one output in a function. The use of math clip art is vital in education because it provides visual models that simplify abstract concepts. For functions, these visuals clarify what constitutes valid versus invalid mappings. |
Relations and Functions |
|
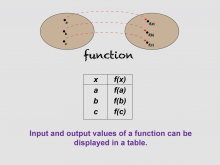
Math Clip Art--Function Concepts--Function Representations 06 | Math Clip Art--Function Concepts--Function Representations 06TopicFunctions DescriptionThis image features a table displaying inputs 'a', 'b', and 'c' mapped to outputs f(a), f(b), and f(c). It visually represents how input and output values of a function can be organized in a tabular format, making it easier to analyze relationships. Educators can use this image to teach students about the organization of function data. By presenting inputs and outputs in a table, students can clearly see how each input corresponds to an output, reinforcing their understanding of functions. |
Relations and Functions |
|
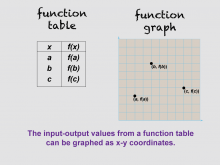
Math Clip Art--Function Concepts--Function Representations 07 | Math Clip Art--Function Concepts--Function Representations 07TopicFunctions DescriptionThis image shows a table with columns for x and f(x) values, alongside a graph plotting these points as (a, f(a)), (b, f(b)), (c, f(c)). It demonstrates how input-output values from a function table can be represented graphically as x-y coordinates. Teachers can use this visual to illustrate the connection between tables and graphs. By plotting points from the table onto a graph, students can better understand how numerical data translates into visual patterns. |
Relations and Functions |
|
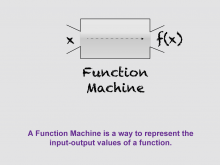
Math Clip Art--Function Concepts--Function Representations 08 | Math Clip Art--Function Concepts--Function Representations 08TopicFunctions DescriptionThis illustration depicts a "Function Machine" with an input x and output f(x). The box labeled "Function Machine" symbolizes how functions process inputs into outputs, representing the concept of functional transformation. This image is helpful for educators explaining the abstract idea of functions as machines that transform inputs into outputs according to specific rules. The use of math clip art is essential in teaching because it provides visual models that make abstract ideas more tangible. Function machines help students visualize the systematic nature of functions. |
Relations and Functions |
|
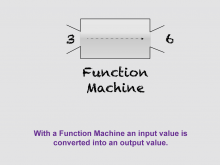
Math Clip Art--Function Concepts--Function Representations 09 | Math Clip Art--Function Concepts--Function Representations 09TopicFunctions DescriptionThis image illustrates a "Function Machine" converting an input value of 3 into an output value of 6. It visually demonstrates how an input is transformed into an output through, for example, multiplication by 2, showcasing functional operations. This visual aids educators in explaining how specific operations within a function machine transform inputs into outputs, emphasizing the rule-based nature of functions. |
Relations and Functions |
|
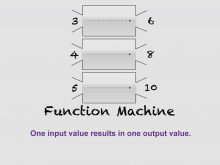
Math Clip Art--Function Concepts--Function Representations 10 | Math Clip Art--Function Concepts--Function Representations 10TopicFunctions DescriptionThis image shows a function machine processing three inputs (3, 4, 5) into corresponding outputs (6, 8, 10). Each input is doubled to produce its output, illustrating consistent functional transformation rules. This visual helps educators demonstrate how consistent rules apply across different inputs within functions, emphasizing predictable outcomes based on established operations. The use of math clip art is vital in education because it provides visual models that clarify complex concepts. Function machines illustrate systematic transformations within functions. |
Relations and Functions |
|
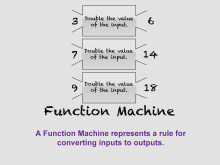
Math Clip Art--Function Concepts--Function Representations 11 | Math Clip Art--Function Concepts--Function Representations 11TopicFunctions DescriptionThis image features a function machine that doubles the value of each input. For example, inputs of 3, 7, and 9 are transformed into outputs of 6, 14, and 18, respectively. This illustrates the consistent rule-based transformation characteristic of functions. Educators can use this visual to explain how function machines apply specific rules to convert inputs into outputs, reinforcing the concept of functional operations. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 12 | Math Clip Art--Function Concepts--Function Representations 12TopicFunctions DescriptionThis image displays three different function machines: one triples the input (3 to 9), another adds 3 (7 to 10), and the third subtracts 5 (9 to 4). These examples illustrate various function rules that transform inputs into outputs. This visual aids educators in demonstrating how different rules can define functions, showcasing the versatility of function machines in applying diverse operations. The use of math clip art is essential in teaching as it provides visual models that clarify abstract processes. Function machines illustrate how different rules can be applied within functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 13 | Math Clip Art--Function Concepts--Function Representations 13TopicFunctions DescriptionThis image illustrates a "Function Machine" with two operations: one doubles the input value, and another adds 2. Arrows visually represent these transformations, demonstrating how multiple operations can be applied sequentially within a function. This visual helps educators explain how knowing the function rule allows for systematic operations on variables, reinforcing the concept of sequential transformations in functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 14 | Math Clip Art--Function Concepts--Function Representations 14TopicFunctions DescriptionThis image shows a function table with columns labeled "x" and "f(x)" alongside a rule stating to multiply each input by 2. The table lists values from 0 to 4 for x and their corresponding outputs as multiples of 2, illustrating pattern recognition in functions. This visual aids educators in teaching students how to identify patterns in input-output values and write corresponding function rules. The use of math clip art is vital in education as it provides visual models that simplify abstract concepts. Tables help students systematically explore patterns within functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 15 | Math Clip Art--Function Concepts--Function Representations 15TopicFunctions DescriptionThis image displays a function table with columns "x" and "f(x)" showing a pattern where each output is the input value plus 3. The function rule is to add 3 to each input value, illustrating how rules can be derived from patterns. This visual helps educators teach students how to recognize patterns in data and formulate corresponding function rules based on consistent transformations. The use of math clip art is crucial in education because it provides visual models that clarify complex ideas. Tables help students identify consistent patterns within functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 16 | Math Clip Art--Function Concepts--Function Representations 16TopicFunctions DescriptionThis image shows a function table with columns labeled x and f(x), paired with a rule stating: "For every input value, multiply by 2 and add 3." Examples are given for inputs from 0 to 4, illustrating how combined operations define functions. This visual aids educators in explaining how multiple operations can define complex function rules, helping students understand layered transformations within functions. The use of math clip art is essential in teaching as it provides visual models that simplify abstract processes. Tables help students explore combined operations within functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 17 | Math Clip Art--Function Concepts--Function Representations 17TopicFunctions DescriptionThis image presents a function rule and equation: "For every input value, multiply it by 2," expressed as f(x)=2x. Examples are provided for inputs from 0 to 3, illustrating how equations represent functional relationships. This visual helps educators teach students how equations can succinctly express function rules, reinforcing algebraic representations of functions. The use of math clip art is crucial in education because it provides visual models that clarify complex ideas. Equations help students understand symbolic representations within functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 18 | Math Clip Art--Function Concepts--Function Representations 18TopicFunctions DescriptionThis image illustrates a function rule and equation. The rule is "For every input value, add 3," and the equation is f(x) = x + 3. Examples for inputs from 0 to 3 demonstrate how the rule consistently transforms inputs into outputs. Educators can use this visual to show how function rules can be expressed algebraically, helping students understand the connection between rules and equations. The use of math clip art is essential in teaching as it provides visual models that simplify abstract processes. Equations help students grasp symbolic representations within functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Function Representations 19 | Math Clip Art--Function Concepts--Function Representations 19TopicFunctions DescriptionThis image illustrates a function rule and its corresponding equation. The rule "For every input value, multiply by 2 and add 3" is shown alongside the equation f(x) = 2x + 3. Examples for inputs from 0 to 3 highlight how these operations transform inputs into outputs. This visual helps educators teach students how complex function rules can be expressed as equations, reinforcing the concept of algebraic representation. |
Relations and Functions |
|
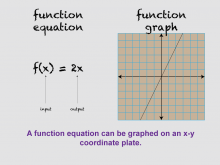
Math Clip Art--Function Concepts--Function Representations 20 | Math Clip Art--Function Concepts--Function Representations 20TopicFunctions DescriptionThis image shows a function equation f(x) = 2x on the left side, labeled with "input" and "output." On the right, it displays a graph of this linear function on an x-y grid, illustrating how equations can be represented graphically. This visual aids educators in demonstrating the connection between algebraic equations and their graphical representations, helping students visualize linear relationships. The use of math clip art is essential in teaching as it provides visual models that make abstract ideas more tangible. Graphs help students understand relationships within functions. |
Relations and Functions |
|
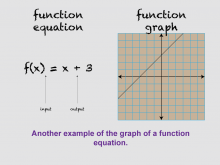
Math Clip Art--Function Concepts--Function Representations 21 | Math Clip Art--Function Concepts--Function Representations 21TopicFunctions DescriptionThis image features a function equation f(x) = x + 3 on the left side, labeled with "input" and "output." On the right, it shows a graph of this linear function on an x-y grid, illustrating how equations translate into graphical form. This visual helps educators explain how algebraic expressions can be represented visually, reinforcing students' understanding of linear functions. The use of math clip art is crucial in education because it provides visual models that simplify complex concepts. Graphs help students visualize relationships within functions. |
Relations and Functions |

|
Math Clip Art--Function Concepts--Properties of Functions 01 | Math Clip Art--Function Concepts--Properties of Functions 01TopicFunctions DescriptionThis image serves as a title card for a series of clip art images focusing on the properties of functions. The title card sets the stage for an in-depth exploration of various function types and their unique characteristics. By using this image as an introduction, educators can effectively prepare students for the visual journey through different function properties. |
Relations and Functions |
|
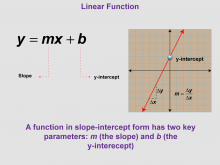
Math Clip Art--Function Concepts--Properties of Functions 02 | Math Clip Art--Function Concepts--Properties of Functions 02TopicFunctions DescriptionThis image illustrates a linear function graph with the equation y = mx + b, highlighting two crucial components: the slope (m) and the y-intercept (b). The visual representation clearly shows how these parameters affect the graph's appearance. The slope, indicated by an arrow, demonstrates the steepness and direction of the line. The y-intercept, marked where the line crosses the y-axis, shows the starting point of the function. |
Relations and Functions |
|
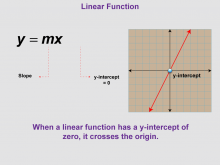
Math Clip Art--Function Concepts--Properties of Functions 03 | Math Clip Art--Function Concepts--Properties of Functions 03TopicFunctions DescriptionThis image depicts a graph of a linear function with the equation y = mx, illustrating a special case where the line passes through the origin. The slope is clearly marked, and the y-intercept is noted as zero. This visual representation helps students understand the relationship between the equation form and the graph's appearance, particularly the significance of the absence of a constant term. |
Relations and Functions |
|
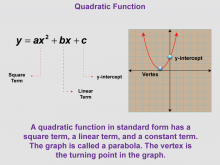
Math Clip Art--Function Concepts--Properties of Functions 04 | Math Clip Art--Function Concepts--Properties of Functions 04TopicFunctions DescriptionThis image illustrates a quadratic function in standard form y = ax² + bx + c, marking the square, linear, and constant terms. The graph shows a parabola with a labeled vertex and y-intercept. This visual representation helps students understand the components of a quadratic function and how they relate to the graph's shape and position. |
Relations and Functions |
|
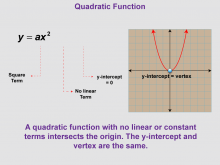
Math Clip Art--Function Concepts--Properties of Functions 05 | Math Clip Art--Function Concepts--Properties of Functions 05TopicFunctions DescriptionThis image depicts a quadratic function y = ax² with no linear or constant terms. It shows a parabola intersecting at the origin, where the y-intercept equals the vertex. This visual representation helps students understand a special case of quadratic functions and how the absence of certain terms affects the graph's position and shape. |
Relations and Functions |
|
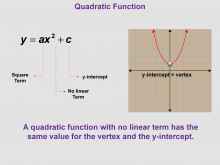
Math Clip Art--Function Concepts--Properties of Functions 06 | Math Clip Art--Function Concepts--Properties of Functions 06TopicFunctions DescriptionThis image shows a quadratic function in the form y = ax² + c. It highlights the square term and indicates there is no linear term. The graph is a parabola with its vertex at the y-intercept. This visual representation helps students understand another special case of quadratic functions and how the absence of the linear term affects the graph's position and shape. |
Relations and Functions |
|
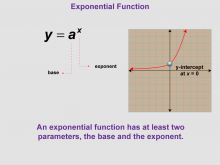
Math Clip Art--Function Concepts--Properties of Functions 07 | Math Clip Art--Function Concepts--Properties of Functions 07TopicFunctions DescriptionThis image displays an exponential function graph with the equation y = aˣ, highlighting the base and exponent. The graph shows a y-intercept at x=0, illustrating a fundamental property of this type of exponential function. This visual representation is crucial for understanding the basic form of exponential functions and how they differ from linear and quadratic functions in terms of growth rate and graph shape. |
Relations and Functions |
|
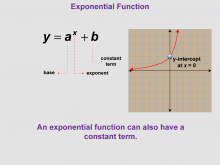
Math Clip Art--Function Concepts--Properties of Functions 08 | Math Clip Art--Function Concepts--Properties of Functions 08TopicFunctions DescriptionThis image illustrates an exponential function graph with the equation y = aˣ + b, highlighting the base, exponent, and constant term. The graph shows a marked y-intercept at x = 0, which is different from the basic exponential function. This visual representation is essential for understanding how the addition of a constant term affects the graph of an exponential function. |
Relations and Functions |
|
Math Example--Function Concepts--Building Functions: Example 1 | Math Example--Function Concepts--Building Functions: Example 1TopicArithmetic DescriptionAnalyze the effect of building a new function f(x + a) from f(x) = x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x shifts horizontally by adding a to the input. substituting a = 1, the new function becomes f(x + a) = x + 1. the graph shifts one unit up. |
Relations and Functions |
|
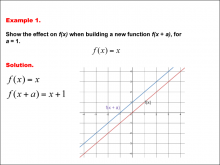
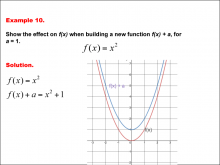
Math Example--Function Concepts--Building Functions: Example 10 | Math Example--Function Concepts--Building Functions: Example 10TopicArithmetic DescriptionAnalyze the effect of building a new function f(x) + a from f(x) = x2, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x2 shifts vertically by adding a to the output. substituting a = 1, the new function becomes f(x) + a = x2 + 1. the graph shifts one unit upward. |
Relations and Functions |
|
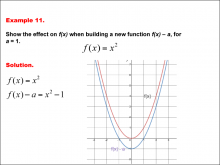
Math Example--Function Concepts--Building Functions: Example 11 | Math Example--Function Concepts--Building Functions: Example 11TopicArithmetic DescriptionThe problem involves analyzing the effect on the function f(x) = x2 when a constant a is subtracted. The specific scenario is for a = 1. The goal is to determine how the graph of f(x) is transformed. This example shows the effect on the function when subtracting a constant a from f(x) shifts the graph of f(x) downward by a units. for a = 1, the function becomes f(x) - a = x2 - 1. this results in a vertical shift down, as shown by the new graph in blue compared to the original in red. |
Relations and Functions |
|
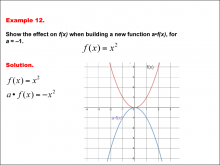
Math Example--Function Concepts--Building Functions: Example 12 | Math Example--Function Concepts--Building Functions: Example 12TopicArithmetic DescriptionThe problem examines the effect on the function f(x) = x2 when it is scaled by a constant a. The specific case here is a = -1. The goal is to describe the transformation caused by the scaling. This example shows the effect on the function when multiplying f(x) by a constant a reflects the graph across the x-axis if a < 0. for a = -1, the function becomes a * f(x) = -x2. this results in a reflection of the original graph (in red) to the inverted graph (in blue). |
Relations and Functions |
|
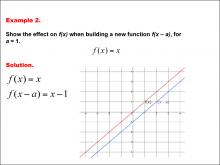
Math Example--Function Concepts--Building Functions: Example 2 | Math Example--Function Concepts--Building Functions: Example 2TopicArithmetic DescriptionAnalyze the effect of building a new function f(x - a) from f(x) = x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x shifts horizontally by subtracting a from the input. substituting a = 1, the new function becomes f(x - a) = x - 1. the graph shifts one unit down. |
Relations and Functions |
|
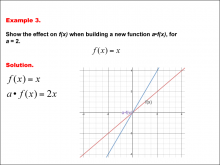
Math Example--Function Concepts--Building Functions: Example 3 | Math Example--Function Concepts--Building Functions: Example 3TopicArithmetic DescriptionAnalyze the effect of building a new function a * f(x) from f(x) = x, where a = 2. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x scales vertically by multiplying the output by a. substituting a = 2, the new function becomes a * f(x) = 2x. the graph is stretched vertically. |
Relations and Functions |
|
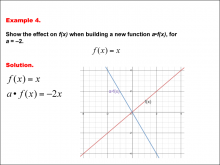
Math Example--Function Concepts--Building Functions: Example 4 | Math Example--Function Concepts--Building Functions: Example 4TopicArithmetic DescriptionAnalyze the effect of building a new function a * f(x) from f(x) = x, where a = -2. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x scales vertically and reflects across the x-axis due to the negative value of a. substituting a = -2, the new function becomes a * f(x) = -2x. the graph is reflected and stretched vertically. |
Relations and Functions |
|
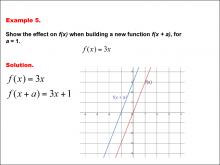
Math Example--Function Concepts--Building Functions: Example 5 | Math Example--Function Concepts--Building Functions: Example 5TopicArithmetic DescriptionAnalyze the effect of building a new function f(x + a) from f(x) = 3x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = 3x shifts horizontally by adding a to the input. substituting a = 1, the new function becomes f(x + a) = 3x + 1. the graph shifts one unit up. |
Relations and Functions |
|
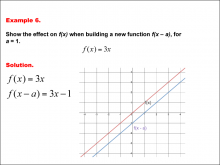
Math Example--Function Concepts--Building Functions: Example 6 | Math Example--Function Concepts--Building Functions: Example 6TopicArithmetic DescriptionAnalyze the effect of building a new function f(x - a) from f(x) = 3x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = 3x shifts horizontally by subtracting a from the input. substituting a = 1, the new function becomes f(x - a) = 3x - 1. the graph shifts one unit down. |
Relations and Functions |
|
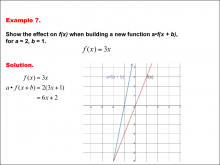
Math Example--Function Concepts--Building Functions: Example 7 | Math Example--Function Concepts--Building Functions: Example 7TopicArithmetic DescriptionAnalyze the effect of building a new function a * f(x + b) from f(x) = 3x, where a = 2 and b = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = 3x first shifts horizontally by adding b to the input, and then scales vertically by a. substituting a = 2 and b = 1, the new function becomes a * f(x + b) = 6x + 2. the graph is shifted and stretched vertically. |
Relations and Functions |
|
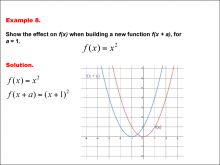
Math Example--Function Concepts--Building Functions: Example 8 | Math Example--Function Concepts--Building Functions: Example 8TopicArithmetic DescriptionAnalyze the effect of building a new function f(x + a) from f(x) = x2, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x2 shifts horizontally by adding a to the input. substituting a = 1, the new function becomes f(x + a) = (x + 1)2. the graph shifts one unit to the left. |
Relations and Functions |
|
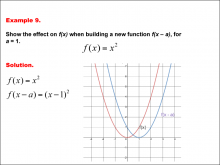
Math Example--Function Concepts--Building Functions: Example 9 | Math Example--Function Concepts--Building Functions: Example 9TopicArithmetic DescriptionAnalyze the effect of building a new function f(x - a) from f(x) = x2, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x2 shifts horizontally by subtracting a from the input. substituting a = 1, the new function becomes f(x - a) = (x - 1)2. the graph shifts one unit to the right. |
Relations and Functions |
|
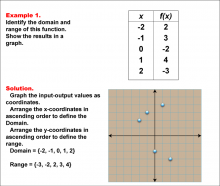
Math Example--Function Concepts--Domain and Range of a Function--Example 1 | Math Example--Function Concepts--Domain and Range of a Function--Example 1TopicArithmetic DescriptionThe example demonstrates identify the domain and range of the given function, represented by a table with input (x) and output (f(x)) values. Graph the function and define the domain and range. This is illustrated by the accompanying image, which shows graph the points based on the (x, f(x)) pairs. For the domain, list the x-coordinates in ascending order: {-2, -1, 0, 1, 2}. For the range, list the y-coordinates in ascending order: {-3, -2, 2, 3, 4}. This solution involves plotting discrete points and organizing the values to clearly define the function's domain and range. |
Relations and Functions |
|
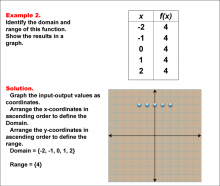
Math Example--Function Concepts--Domain and Range of a Function--Example 2 | Math Example--Function Concepts--Domain and Range of a Function--Example 2TopicArithmetic DescriptionThe example demonstrates identify the domain and range of a function with constant output, represented by a table of input (x) values and constant output (f(x) = 4). Graph the function and determine domain and range. This is illustrated by the accompanying image, which shows graph the points where x-values vary but f(x) remains constant. The domain is the set of x-values in ascending order: {-2, -1, 0, 1, 2}. The range consists only of the single value {4}, as f(x) remains constant. The graph illustrates a horizontal line, reflecting the function's single output value. |
Relations and Functions |
|
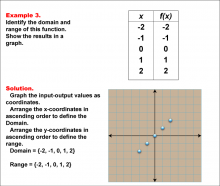
Math Example--Function Concepts--Domain and Range of a Function--Example 3 | Math Example--Function Concepts--Domain and Range of a Function--Example 3TopicArithmetic DescriptionThe example demonstrates determine the domain and range for a linear function with equal input and output values. display results in a graph and identify the domain and range. This is illustrated by the accompanying image, which shows plot points using the input-output pairs. the domain is the x-coordinates in ascending order: {-2, -1, 0, 1, 2}. The range matches the domain as it mirrors the values of x: {-2, -1, 0, 1, 2}. This function demonstrates a one-to-one correspondence between x and f(x), resulting in identical domain and range values. |
Relations and Functions |
|
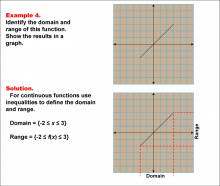
Math Example--Function Concepts--Domain and Range of a Function--Example 4 | Math Example--Function Concepts--Domain and Range of a Function--Example 4TopicArithmetic DescriptionThe example demonstrates determine the domain and range of a continuous linear function, graph it, and describe the domain and range using inequalities. This is illustrated by the accompanying image, which shows for a continuous function, use inequalities. The domain is defined as -2 ≤ x ≤ 3. The range is defined as -2 ≤ f(x) ≤ 3. The solution includes a graph with a continuous line segment and a boxed outline showing the region that encompasses the domain and range on the coordinate grid. |
Relations and Functions |
|
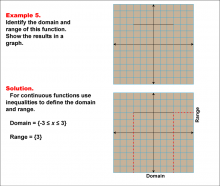
Math Example--Function Concepts--Domain and Range of a Function--Example 5 | Math Example--Function Concepts--Domain and Range of a Function--Example 5TopicArithmetic DescriptionThe example demonstrates identify the domain and range of a horizontal line function where f(x) = 3. Represent the results on a graph and describe the domain and range using inequalities. This is illustrated by the accompanying image, which shows since f(x) remains constant, the graph displays a horizontal line at f(x) = 3. The domain covers the x-values from -3 to 3, written as -3 ≤ x ≤ 3. The range consists only of the constant value {3}, as f(x) does not vary. This scenario illustrates a function with an interval-based domain and a single-point range. |
Relations and Functions |
|
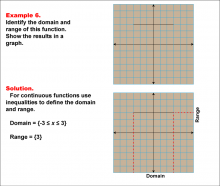
Math Example--Function Concepts--Domain and Range of a Function--Example 6 | Math Example--Function Concepts--Domain and Range of a Function--Example 6TopicArithmetic |
Relations and Functions |