
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 19: Tables, Equations, and Graphs, Oh My!
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
VIDEO: Algebra Applications: Functions and Relations | VIDEO: Algebra Applications: Functions and Relations
TopicFunctions and Relations |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
VIDEO: Algebra Nspirations: Functions and Relations | VIDEO: Algebra Nspirations: Functions and Relations
TopicFunctions and Relations |
Applications of Functions and Relations, Quadratic Equations and Functions and Relations and Functions |

|
Closed Captioned Video: Algebra Applications: Functions and Relations | Closed Captioned Video: Algebra Applications: Functions and RelationsTopicFunctions and Relations |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Applications: Functions and Relations, 1 | Closed Captioned Video: Algebra Applications: Functions and Relations, 1TopicFunctions and Relations |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Applications: Functions and Relations, 2 | Closed Captioned Video: Algebra Applications: Functions and Relations, 2TopicFunctions and Relations |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Applications: Functions and Relations, 3 | Closed Captioned Video: Algebra Applications: Functions and Relations, 3TopicFunctions and Relations DescriptionThis segment focuses on the circular orbit of the Orion capsule around Earth as it docks with the International Space Station. Key concepts include the circle as a conic section and its equation. Parametric equations with sine and cosine functions are introduced to model periodic motion. Applications involve understanding how the capsule maintains a stable orbit, completes periodic motion every 90 minutes, and prepares for the Mars journey. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Applications: Functions and Relations, 4 | Closed Captioned Video: Algebra Applications: Functions and Relations, 4TopicFunctions and Relations DescriptionThis segment describes the elliptical paths of Earth and Mars around the sun and how the Orion capsule follows a transfer ellipse to reach Mars. Key concepts include ellipses as conic sections, their equations, eccentricity, and quadratic relations. Applications involve modeling planetary orbits and calculating orbital equations using data like eccentricity and semi-major axis values. The segment also explores graphing ellipses with tools like the TI-Nspire. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Nspirations: Functions and Relations | Closed Captioned Video: Algebra Nspirations: Functions and Relations
Functions are relationships between quantities that change. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video explores the definition of a function, its vocabulary and notations, and distinguishes the concept of function from a general relation. Multiple representations of functions are provided using the TI-Nspire, while dynamic visuals and scenarios put them into real-world contexts. Concepts explored: functions, relations, equations, quadratic functions, linear functions, multiple representations. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Nspirations: Functions and Relations, 1 | Closed Captioned Video: Algebra Nspirations: Functions and Relations, Segment 1
In this Investigation we explore the definition of a Relation. This video is Segment 1 of a 4 segment series related to Functions and Relations. Segments 1 and 2 are grouped together. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Nspirations: Functions and Relations, 3 | Closed Captioned Video: Algebra Nspirations: Functions and Relations, Segment 3
In this Investigation we look at functions. This video is Segment 3 of a 4 segment series related to Functions and Relations. Segments 3 and 4 are grouped together. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |
|
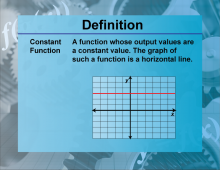
Definition--Functions and Relations Concepts--Constant Function | Constant FunctionTopicFunctions and Relations DefinitionA constant function is a function that always returns the same value, no matter the input. DescriptionThe constant function is one of the simplest types of functions in mathematics, expressed as f(x) = c |
Relations and Functions |
|
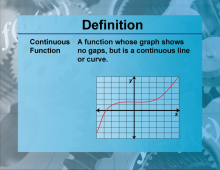
Definition--Functions and Relations Concepts--Continuous Function | Continuous FunctionTopicFunctions and Relations DefinitionA continuous function is a function that does not have any breaks, holes, or gaps in its domain. DescriptionContinuous functions are fundamental in calculus and mathematical analysis because they allow for the application of limits, derivatives, and integrals. A function f(x) is continuous if, for every point 𝑐 c in its domain, lim x→c f(x) = f(c) |
Relations and Functions |
|
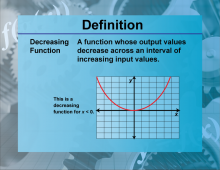
Definition--Functions and Relations Concepts--Decreasing Function | Decreasing FunctionTopicFunctions and Relations DefinitionA decreasing function is a function where the value of the function decreases as the input increases. DescriptionDecreasing functions are important in mathematics because they describe scenarios where an increase in one variable leads to a decrease in another. This is mathematically represented as f(x1) > f(x2) for any 𝑥1 < 𝑥2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Dependent Variable | Dependent VariableTopicFunctions and Relations DefinitionA dependent variable is a variable whose value depends on one or more other variables. |
Relations and Functions |
|
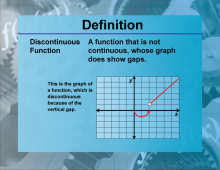
Definition--Functions and Relations Concepts--Discontinuous Function | Discontinuous FunctionTopicFunctions and Relations DefinitionA discontinuous function is a function that has one or more points where it is not continuous. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Distorting a Function Horizontally | Distorting a Function HorizontallyTopicFunctions and Relations DefinitionDistorting a function horizontally involves stretching or compressing the graph of the function along the x-axis. DescriptionHorizontal distortions of functions are significant because they alter the input values while maintaining the overall shape of the graph. This is mathematically represented as f(kx) where k is a constant. If k > 1, the function compresses horizontally, and if 0 < 𝑘 < 1, it stretches. |
Relations and Functions |
|
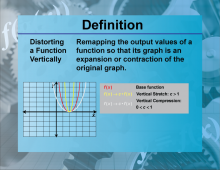
Definition--Functions and Relations Concepts--Distorting a Function Vertically | Distorting a Function VerticallyTopicFunctions and Relations DefinitionDistorting a function vertically involves stretching or compressing the graph of the function along the y-axis. DescriptionVertical distortions of functions are significant because they alter the output values while maintaining the overall shape of the graph. This is mathematically represented as kf(x) |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Domain of a Function | Domain of a FunctionTopicFunctions and Relations DefinitionThe domain of a function is the set of all possible input values (x-values) for which the function is defined. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Even Function | Even FunctionTopicFunctions and Relations DefinitionAn even function is a function that satisfies the condition f(x) = f(−x) for all x in its domain. DescriptionEven functions are important in mathematics because they exhibit symmetry about the y-axis. This property is useful in various fields, including physics and engineering, where symmetry simplifies analysis and problem-solving. For example, the function f(x)=x2 |
Relations and Functions |
|
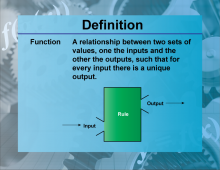
Definition--Functions and Relations Concepts--Function | FunctionTopicFunctions and Relations DefinitionA function is a relation that uniquely associates each element of a set with exactly one element of another set. |
Relations and Functions |
|
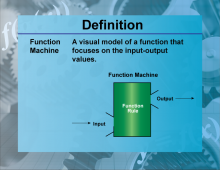
Definition--Functions and Relations Concepts--Function Machine | Function MachineTopicFunctions and Relations DefinitionA function machine is a conceptual tool used to understand how functions work by visualizing inputs and outputs. DescriptionThe function machine is a useful educational tool that helps students grasp the concept of functions by visualizing the process of converting inputs into outputs. It emphasizes the idea that a function takes an input, processes it according to a specific rule, and produces an output. For example, if the function is f(x) = x + 2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Function Notation | Function NotationTopicFunctions and Relations DefinitionFunction notation is a way to represent functions in the form f(x), where f denotes the function and x denotes the input variable. DescriptionFunction notation is a standardized way to write functions, making it easier to understand and communicate mathematical relationships. It is widely used in algebra, calculus, and other branches of mathematics. For example, the notation f(x) = x2 |
Relations and Functions |
|
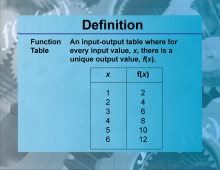
Definition--Functions and Relations Concepts--Function Table | Function TableTopicFunctions and Relations DefinitionA function table is a table that lists input values and their corresponding output values for a given function. DescriptionFunction tables are useful tools in mathematics for organizing and analyzing the relationship between inputs and outputs of a function. They help in visualizing how a function behaves and in identifying patterns. For example, a function table for f(x) = 2x + 1 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Graphs of Functions | Graphs of FunctionsTopicFunctions and Relations DefinitionGraphs of functions are visual representations of the relationship between input values and output values of a function. DescriptionGraphs of functions are essential tools in mathematics for visualizing how a function behaves. They provide a clear picture of the relationship between the input and output values, making it easier to analyze and interpret the function. For example, the graph of f(x) = x2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Graphs of Relations | Graphs of RelationsTopicFunctions and Relations DefinitionGraphs of relations are visual representations of the relationship between two sets of values, not necessarily functions. |
Relations and Functions |
|
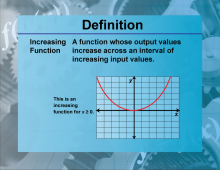
Definition--Functions and Relations Concepts--Increasing Function | Increasing FunctionTopicFunctions and Relations DefinitionAn increasing function is a function where the value of the function increases as the input increases. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Independent Variable | Independent VariableTopicFunctions and Relations DefinitionAn independent variable is a variable that represents the input or cause and is manipulated to observe its effect on the dependent variable. |
Relations and Functions |
|
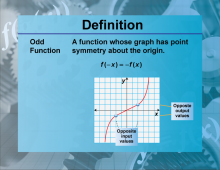
Definition--Functions and Relations Concepts--Odd Function | Odd FunctionTopicFunctions and Relations DefinitionAn odd function is a function that satisfies the condition f(−x) = −f(x) for all x in its domain. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Parametric Equations | Parametric EquationsTopicFunctions and Relations DefinitionParametric equations are a set of equations that express the coordinates of the points of a curve as functions of a variable called a parameter. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Range of a Function | Range of a FunctionTopicFunctions and Relations DefinitionThe range of a function is the set of all possible output values (y-values) that the function can produce. DescriptionUnderstanding the range of a function is crucial in mathematics because it defines the scope of possible outputs. The range is determined by the function's rule and the domain. For example, the range of the function f(x) = x2 |
Relations and Functions |
|
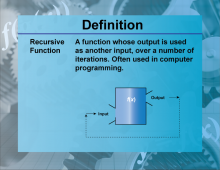
Definition--Functions and Relations Concepts--Recursive Function | Recursive FunctionTopicFunctions and Relations DefinitionA recursive function is a function that calls itself in its definition. DescriptionRecursive functions are important in mathematics and computer science because they provide a way to solve problems by breaking them down into simpler sub-problems. They are defined by a base case and a recursive case. For example, the factorial function f(n) = n⋅f(n−1) with f(0)=1 |
Relations and Functions |
|
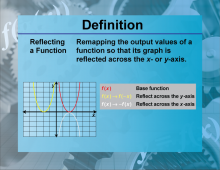
Definition--Functions and Relations Concepts--Reflecting a Function | Reflecting a FunctionTopicFunctions and Relations DefinitionReflecting a function involves flipping the graph of the function over a specified axis. DescriptionReflecting functions is significant in mathematics because it helps in understanding the symmetry and transformations of functions. A function can be reflected over the x-axis or y-axis, changing its orientation. For example, reflecting the function f(x) = x2 |
Relations and Functions |
|
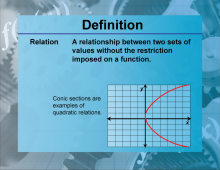
Definition--Functions and Relations Concepts--Relation | RelationTopicFunctions and Relations DefinitionA relation is a set of ordered pairs, where each element from one set is paired with an element from another set. |
Relations and Functions |
|
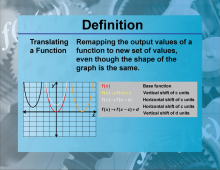
Definition--Functions and Relations Concepts--Translating a Function | Translating a FunctionTopicFunctions and Relations DefinitionTranslating a function involves shifting the graph of the function horizontally, vertically, or both, without changing its shape. DescriptionTranslating functions is significant in mathematics because it helps in understanding how functions behave under shifts. A function can be translated horizontally by adding or subtracting a constant to the input, and vertically by adding or subtracting a constant to the output. For example, translating the function f(x) = x2 horizontally by 2 units results in |
Relations and Functions |
|
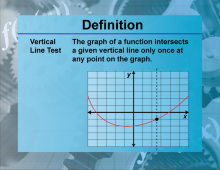
Definition--Functions and Relations Concepts--Vertical Line Test | Vertical Line TestTopicFunctions and Relations DefinitionThe vertical line test is a method used to determine if a graph represents a function by checking if any vertical line intersects the graph more than once. DescriptionThe vertical line test is important in mathematics because it helps in identifying whether a given graph represents a function. If a vertical line intersects the graph at more than one point, then the graph does not represent a function. This test is used in various fields, including computer science for validating functions in programming and in mathematics for analyzing graphs. For example, the graph of |
Relations and Functions |
|
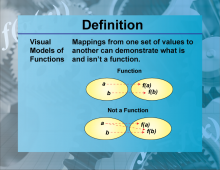
Definition--Functions and Relations Concepts--Visual Models of Functions | Visual Models of FunctionsTopicFunctions and Relations DefinitionVisual models of functions are graphical representations that illustrate the relationship between input and output values of functions. DescriptionVisual models of functions are important in mathematics because they provide a clear and intuitive way to understand how functions behave. These models include graphs, tables, and diagrams that show the relationship between input and output values. For example, the graph of f(x) = x2 |
Relations and Functions |
|
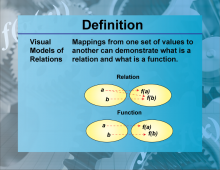
Definition--Functions and Relations Concepts--Visual Models of Relations | Visual Models of RelationsTopicFunctions and Relations DefinitionVisual models of relations are graphical representations that illustrate the relationship between two sets of values, not necessarily functions. |
Relations and Functions |
|
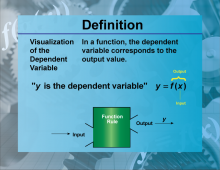
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable | Visualization of the Dependent VariableTopicFunctions and Relations DefinitionVisualization of the dependent variable involves graphically representing the outcomes or responses that depend on the independent variable. |
Relations and Functions |
|
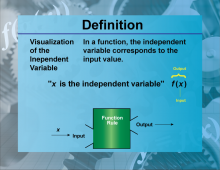
Definition--Functions and Relations Concepts--Visualization of the Independent Variable | Visualization of the Independent VariableTopicFunctions and Relations DefinitionVisualization of the independent variable involves graphically representing the variable that is manipulated to observe its effect on the dependent variable. |
Relations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Evaluating Functions | INSTRUCTIONAL RESOURCE: Tutorial: Evaluating Functions
In this Slide Show, learn what it means to evaluate a function. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Functions and Relations and Relations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Are the Domain and Range? | INSTRUCTIONAL RESOURCE: Tutorial: What Are the Domain and Range?
In this Slide Show, learn about domain and range. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.< Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Functions and Relations and Relations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Is a Function? | INSTRUCTIONAL RESOURCE: Tutorial: What Is a Function?
In this Slide Show, learn what a function is. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.< Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Functions and Relations and Relations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Is a Recursive Function? | INSTRUCTIONAL RESOURCE: Tutorial: What Is a Recursive Function?
In this Slide Show, learn what a recursive function is. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.< Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Functions and Relations and Relations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Is Function Notation? | INSTRUCTIONAL RESOURCE: Tutorial: What Is Function Notation?
In this Slide Show, learn about funciton notation in the context of evaluating or transforming a function. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.< Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Functions and Relations and Relations and Functions |

|
Math Clip Art--Function Concepts--Function Graphs 01 | Math Clip Art--Function Concepts--Function Graphs 01TopicFunctions DescriptionThis image serves as a title card for a collection of 9 math clip art images on function graphs. It features a pencil on a graph showing a curve intersecting the axes, labeled with points A and B. This visual representation introduces the concept of functions and their graphical depiction, setting the stage for a deeper exploration of function graphs. |
Relations and Functions |
|
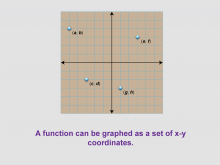
Math Clip Art--Function Concepts--Function Graphs 02 | Math Clip Art--Function Concepts--Function Graphs 02TopicFunctions DescriptionThis image presents a graph with points labeled (a, b), (c, d), (e, f), and (g, h) without connecting lines. It illustrates that a function can be graphed as a set of x-y coordinates, emphasizing the discrete nature of data points in a function. |
Relations and Functions |
|
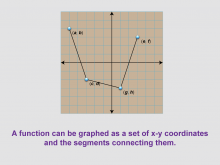
Math Clip Art--Function Concepts--Function Graphs 03 | Math Clip Art--Function Concepts--Function Graphs 03TopicFunctions DescriptionThis image showcases a graph with points labeled (a, b), (c, d), (e, f), and (g, h) connected by line segments. It demonstrates that a function can be graphed as a set of x-y coordinates with the segments connecting them, illustrating a step towards continuous function representation. |
Relations and Functions |
|
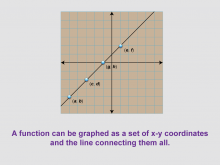
Math Clip Art--Function Concepts--Function Graphs 04 | Math Clip Art--Function Concepts--Function Graphs 04TopicFunctions DescriptionThis image depicts a grid with a straight line connecting four points labeled (a, b), (c, d), (e, f), and (g, h). It illustrates that a function can be graphed as a set of x-y coordinates with a line connecting them all, representing a linear function. The straight line passing through all the labeled points introduces the concept of linear functions. This visualization helps students understand how a continuous straight line can represent a function, with each point on the line corresponding to an input-output pair. It's an excellent tool for discussing linear relationships, slope, and the equation of a line. |
Relations and Functions |
|
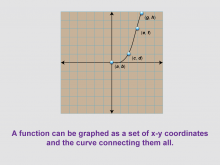
Math Clip Art--Function Concepts--Function Graphs 05 | Math Clip Art--Function Concepts--Function Graphs 05TopicFunctions DescriptionThis image shows a grid with a curve passing through four points labeled (a, b), (c, d), (e, f), and (g, h). It demonstrates that a function can be graphed as a set of x-y coordinates with a curve connecting them all, representing a non-linear function. |
Relations and Functions |
|
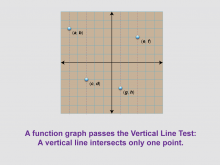
Math Clip Art--Function Concepts--Function Graphs 06 | Math Clip Art--Function Concepts--Function Graphs 06TopicFunctions DescriptionThis image presents a grid with four points labeled (a, b), (c, d), (e, f), and (g, h), with vertical dashed lines passing through each point. It illustrates the Vertical Line Test, a crucial concept in determining whether a graph represents a function. The vertical dashed lines passing through each point introduce the Vertical Line Test, which states that a graph represents a function if any vertical line intersects the graph at most once. This visualization helps students understand a fundamental property of functions: for each input value (x-coordinate), there is only one output value (y-coordinate). |
Relations and Functions |