
Illustrative Math Alignment: Grade 6 Unit 7
Rational Numbers
Lesson 5: Using Negative Numbers to Make Sense of Contexts
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
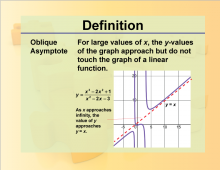
Definition--Rationals and Radicals--Oblique Asymptote | Oblique AsymptoteTopicRationals and Radicals DefinitionAn oblique asymptote is a diagonal line that the graph of a function approaches as the input values become very large or very small. DescriptionOblique Asymptotes are important in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions where the degree of the numerator is one more than the degree of the denominator. For example, the function $$f(x) = \frac{x^2 + 1}{x}$$ |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Partial Fraction Decomposition of a Rational ExpressionTopicRationals and Radicals DefinitionPartial fraction decomposition is a method used to express a rational expression as a sum of simpler fractions. DescriptionPartial Fraction Decomposition is a powerful tool in the study of Rational Numbers, Expressions, Equations, and Functions. It involves breaking down a complex rational expression into a sum of simpler fractions, which are easier to integrate or differentiate. For example, the rational function $$\frac{2x+3}{(x+1)(x-2)}$$ can be decomposed into |
Rational Expressions |

|
Definition--Rationals and Radicals--Radical Equations | Radical EquationsTopicRationals and Radicals DefinitionRadical equations are equations in which the variable is inside a radical, such as a square root or cube root. DescriptionRadical Equations are a fundamental aspect of Radical Numbers, Expressions, Equations, and Functions. These equations involve variables within radical signs, such as square roots or cube roots. Solving radical equations typically requires isolating the radical on one side of the equation and then squaring both sides to eliminate the radical. For example, to solve $$\sqrt{x+3} = 5$$ one would square both sides to obtain $$x + 3 = 25$$ |
Radical Functions and Equations |

|
Definition--Rationals and Radicals--Radical Expression | Radical ExpressionTopicRationals and Radicals DefinitionA radical expression is an expression that contains a radical symbol, which indicates the root of a number. DescriptionRadical Expressions are a core component of Radical Numbers, Expressions, Equations, and Functions. These expressions involve roots, such as square roots, cube roots, or higher-order roots, and are denoted by the radical symbol (√). For example, the expression $$\sqrt{16}$$ |
Radical Expressions |

|
Definition--Rationals and Radicals--Radical Function | Radical FunctionTopicRationals and Radicals DefinitionA radical function is a function that contains a radical expression with the independent variable in the radicand. DescriptionRadical Functions are a vital part of Radical Numbers, Expressions, Equations, and Functions. These functions involve radicals, such as square roots or cube roots, with the independent variable inside the radical. For example, the function $$f(x) = \sqrt{x}$$ |
Radical Expressions |

|
Definition--Rationals and Radicals--Radical Symbol | Radical SymbolTopicRationals and Radicals DefinitionThe radical symbol (√) is used to denote the root of a number, such as a square root or cube root. DescriptionThe Radical Symbol is a fundamental notation in the study of Radical Numbers, Expressions, Equations, and Functions. This symbol (√) indicates the root of a number, with the most common being the square root. For example, the expression $$\sqrt{25}$$ |
Radical Expressions |

|
Definition--Rationals and Radicals--Radicand | RadicandTopicRationals and Radicals DefinitionThe radicand is the number or expression inside the radical symbol that is being rooted. DescriptionThe Radicand is a key component in the study of Radical Numbers, Expressions, Equations, and Functions. It is the number or expression inside the radical symbol that is being rooted. For example, in the expression $$\sqrt{49}$$ |
Radical Expressions |

|
Definition--Rationals and Radicals--Rational Equations | Rational EquationsTopicRationals and Radicals DefinitionRational equations are equations that involve rational expressions, which are fractions containing polynomials in the numerator and denominator. DescriptionRational Equations are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These equations involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Solving rational equations typically requires finding a common denominator, clearing the fractions, and then solving the resulting polynomial equation. For example, to solve $$\frac{1}{x} + \frac{1}{x+1} = \frac{1}{2}$$ |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Rational Exponent | Rational ExponentTopicRationals and Radicals DefinitionA rational exponent is an exponent that is a fraction, where the numerator indicates the power and the denominator indicates the root. DescriptionRational Exponents are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. These exponents are fractions, where the numerator indicates the power and the denominator indicates the root. For example, the expression $$a^{m/n}$$ can be rewritten as $$\sqrt[n]{a^m}$$ |
Rational Expressions |

|
Definition--Rationals and Radicals--Rational Expressions | Rational ExpressionsTopicRationals and Radicals DefinitionRational expressions are fractions in which the numerator and/or the denominator are polynomials. DescriptionRational Expressions are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These expressions are fractions where the numerator and/or the denominator are polynomials. Simplifying rational expressions often involves factoring the polynomials and canceling common factors. For example, the rational expression $$\frac{x^2 - 1}{x - 1}$$ can be simplified to x + 1, provided that $$x \neq 1$$ |
Rational Expressions |

|
Definition--Rationals and Radicals--Rational Functions | Rational FunctionsTopicRationals and Radicals DefinitionRational functions are functions that are the ratio of two polynomials. DescriptionRational Functions are a key concept in the study of Rational Numbers, Expressions, Equations, and Functions. These functions are the ratio of two polynomials, such as $$f(x) = \frac{P(x)}{Q(x)}$$ where P(x) and Q(x) are polynomials. Understanding rational functions involves analyzing their behavior, including identifying asymptotes, intercepts, and discontinuities. For example, the function $$f(x) = \frac{1}{x}$$ |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Rational Numbers | Rational NumbersTopicRationals and Radicals DefinitionRational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Rationalizing a Radical | Rationalizing a RadicalTopicRationals and Radicals DefinitionRationalizing a radical is the process of eliminating radicals from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. DescriptionRationalizing a Radical is an important technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves eliminating radicals from the denominator of a fraction, which simplifies the expression and often makes it easier to work with or compare to other expressions. For example, to rationalize the denominator of $$\frac{1}{\sqrt{3}}$$ |
Radical Expressions |

|
Definition--Rationals and Radicals--Rationalizing the Denominator | Rationalizing the DenominatorTopicRationals and Radicals DefinitionRationalizing the denominator is the process of eliminating radicals or complex numbers from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. DescriptionRationalizing the Denominator is a crucial technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves removing radicals or complex numbers from the denominator of a fraction, which simplifies the expression and often makes it easier to evaluate or compare with other expressions. For example, to rationalize the denominator of |
Radical Expressions |

|
Definition--Rationals and Radicals--Simplifying a Radical Expression | Simplifying a Radical ExpressionTopicRationals and Radicals DefinitionSimplifying a radical expression involves reducing the expression to its simplest form by factoring the radicand and removing any perfect square factors (for square roots) or perfect cube factors (for cube roots). DescriptionSimplifying a Radical Expression is a fundamental skill in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves reducing a radical expression to its simplest form, which often makes it easier to work with and understand. For example, simplifying $$\sqrt{18}$$ results in |
Radical Expressions |

|
Definition--Rationals and Radicals--Simplifying a Rational Expression | Simplifying a Rational ExpressionTopicRationals and Radicals DefinitionSimplifying a rational expression involves reducing the fraction to its lowest terms by factoring both the numerator and denominator and canceling common factors. DescriptionSimplifying a Rational Expression is a crucial skill in the study of Rational Numbers, Expressions, Equations, and Functions. This process involves reducing a rational expression to its simplest form by factoring both the numerator and denominator and canceling common factors. For example, simplifying $$\frac{x^2 - 1}{x - 1}$$ results in x + 1 for |
Rational Expressions |

|
Definition--Rationals and Radicals--Square Root | Square RootTopicRationals and Radicals DefinitionThe square root of a number is a value that, when multiplied by itself, gives the number. It is denoted by the radical symbol √. |
Radical Expressions |
|
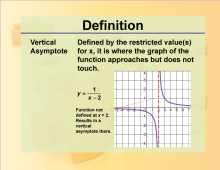
Definition--Rationals and Radicals--Vertical Asymptote | Vertical AsymptoteTopicRationals and Radicals DefinitionA vertical asymptote is a vertical line that the graph of a function approaches but never reaches as the input values get closer to a certain point. DescriptionVertical Asymptotes are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions when the denominator equals zero for certain input values, causing the function to approach infinity or negative infinity. For example, the function $$f(x) = \frac{1}{x-2}$$ |
Rational Functions and Equations |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 1 | Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 1TopicGeometric Models |
Applications of Surface Area and Volume and Rational Functions and Equations |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2 | Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2TopicGeometric Models |
Surface Area, Volume and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Tutorial: Adding and Subtracting Rational Numbers | INSTRUCTIONAL RESOURCE: Tutorial: Adding and Subtracting Rational Numbers
In this Slide Show, learn how to add and subtract rational numbers. Includes links to several Media4Math videos and a math game. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Expressions and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Rational Functions | INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Rational Functions
In this Slide Show, use the Desmos graphing calculator to explore rational functions. To see the complete collection of Desmos Resources click on this link. Note: The download is a PPT file. This is part of a collection of Desmos tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 23 | INSTRUCTIONAL RESOURCE: Math Examples--Graphs of Rational Functions
The complete set of 28 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 44 | INSTRUCTIONAL RESOURCE: Math Examples--Rational Expressions
The complete set of 28 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Expressions and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 45 | INSTRUCTIONAL RESOURCE: Math Examples--Rational Functions in Tabular and Graph Form
This set of tutorials provides 28 examples of rational functions in tabular and graph form. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Expressions and Rational Functions and Equations |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 8)--Lesson 1--Understanding Ratios, Proportional Relationships, and Rational Numbers | Lesson Plan: Ratios and Proportional Relationships In this lesson, students explore ratios and proportional relationships, building on their prior knowledge to deepen their understanding of proportional reasoning. They will analyze proportional relationships in tables, graphs, and equations while identifying the constant of proportionality and its significance in real-world applications. Key concepts covered in this lesson include: |
Ratios and Rates, Percents and Proportions |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 8)--Lesson 1--Understanding Ratios, Proportional Relationships, and Rational Numbers | Lesson Plan: Ratios and Proportional Relationships In this lesson, students explore ratios and proportional relationships, building on their prior knowledge to deepen their understanding of proportional reasoning. They will analyze proportional relationships in tables, graphs, and equations while identifying the constant of proportionality and its significance in real-world applications. Key concepts covered in this lesson include: |
Ratios and Rates, Percents and Proportions |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 8)--Lesson 1--Understanding Ratios, Proportional Relationships, and Rational Numbers | Lesson Plan: Ratios and Proportional Relationships In this lesson, students explore ratios and proportional relationships, building on their prior knowledge to deepen their understanding of proportional reasoning. They will analyze proportional relationships in tables, graphs, and equations while identifying the constant of proportionality and its significance in real-world applications. Key concepts covered in this lesson include: |
Ratios and Rates, Percents and Proportions |

|
Math Clip Art--Function Concepts--Graphs of Functions and Relations--Rational Function Graph | Math Clip Art--Function Concepts--Graphs of Functions and Relations--Rational Function GraphTopicFunctions DescriptionThis clip art depicts a rational function graph. Rational functions are quotients of polynomials and can have a wide variety of shapes depending on the degrees of the numerator and denominator. They generally pass the vertical line test and are thus functions, though they may have discontinuities. |
Rational Functions and Equations |
|
Math Clip Art--Number Systems--Rational Numbers 01 | Math Clip Art--Number Systems--Rational Numbers 01
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 02 | Math Clip Art--Number Systems--Rational Numbers 02
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 03 | Math Clip Art--Number Systems--Rational Numbers 03
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 04 | Math Clip Art--Number Systems--Rational Numbers 04
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 05 | Math Clip Art--Number Systems--Rational Numbers 05
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 06 | Math Clip Art--Number Systems--Rational Numbers 06
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 07 | Math Clip Art--Number Systems--Rational Numbers 07
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |
|
Math Clip Art--Number Systems--Rational Numbers 08 | Math Clip Art--Number Systems--Rational Numbers 08
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |
|
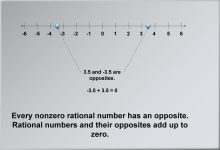
Math Clip Art--Number Systems--Rational Numbers 09 | Math Clip Art--Number Systems--Rational Numbers 09
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 10 | Math Clip Art--Number Systems--Rational Numbers 10
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Clip Art--Number Systems--Rational Numbers 11 | Math Clip Art--Number Systems--Rational Numbers 11
This is part of a collection of math clip art images about different number systems. Included are integers, rational numbers, and real numbers. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 1 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 1TopicExponents DescriptionShows Example 1 with the expression 32. The solution explains how to simplify by multiplying 3 by itself according to the exponent. Example 1: Simplify 32. Multiply 3 by itself two times: 3•3 = 9. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 10 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 10TopicExponents DescriptionShows Example 10 with the expression (-3)3•54. The solution uses order of operations to evaluate each term before multiplying. Example 10: Simplify (-3)3•54. Evaluate each exponential term separately, then multiply: -27•625= -16,875. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 11 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 11TopicExponents DescriptionExample 11 shows how to simplify (1/2)2. The image illustrates multiplying 1/2 by itself due to the exponent of 2. Example 11: Simplify (1/2)2. Multiply one-half two times. Solution: (1/2) * (1/2) = 1/4. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 12 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 12TopicExponents DescriptionExample 12 shows how to simplify (1/3)4. The image illustrates multiplying 1/3 four times due to the exponent of 4. Example 12: Simplify (1/3)4. Multiply one-third four times. Solution: (1/3) * (1/3) * (1/3) * (1/3) = 1/81. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 13 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 13TopicExponents DescriptionExample 13 shows how to simplify (-1/3)3. The image illustrates multiplying -1/3 three times due to the exponent of 3. Example 13: Simplify (-1/3)3. Multiply negative one-third three times. Solution: (-1/3) * (-1/3) * (-1/3) = -1/27. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 14 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 14TopicExponents DescriptionExample 14 shows how to simplify 2-1. The image illustrates rewriting 2-1 as the reciprocal of 2 raised to the first power. Example 14: Simplify 2-1. Negative exponents are written as reciprocals. Solution: 2-1 = 1/2. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 15 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 15TopicExponents DescriptionExample 15 shows how to simplify 2-2. The image illustrates rewriting 2-2 as the reciprocal of 2 raised to the second power. Example 15: Simplify 2-2. Negative exponents are written as reciprocals. Solution: 2-2 = 1/(22) = 1/4. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 2 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 2TopicExponents DescriptionShows Example 2 with the expression 43. The solution explains the simplification by multiplying 4 three times. Example 2: Simplify 43. Multiply 4 by itself three times: 4•4•4 = 64. In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 3 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 3TopicExponents DescriptionShows Example 3 with the expression 54. The solution details multiplying 5 four times. Example 3: Simplify 54. Multiply 5 by itself four times: 5•5•5•5 = 625. In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 4 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 4TopicExponents DescriptionShows Example 4 with the expression 106. The solution simplifies by multiplying 10 six times. Example 4: Simplify 106. Multiply 10 by itself six times: 10•10•10•10•10•10 = 1,000,000. |
Numerical Expressions |