
Illustrative Math Alignment: Grade 6 Unit 8
Data Sets and Distributions
Lesson 15: Quartiles and Interquartile Range
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Definition--Measures of Central Tendency--Quartile | QuartileTopicStatistics DefinitionQuartiles divide a ranked data set into four equal parts. DescriptionQuartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends. |
Data Analysis |
|
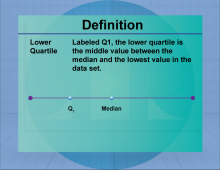
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Upper Quartile | Upper QuartileTopicStatistics DefinitionThe upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. DescriptionThe upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Range of a Data Set 1 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Range of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Range of a Data Set 2 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Range of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Range of a Data Set 3 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Range of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Range of a Data Set 4 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Range of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Range of a Data Set 5 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Range of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 1 | Math Example--Measures of Central Tendency--Range: Example 1TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 2 | Math Example--Measures of Central Tendency--Range: Example 2TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 3 | Math Example--Measures of Central Tendency--Range: Example 3TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 4 | Math Example--Measures of Central Tendency--Range: Example 4TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 5 | Math Example--Measures of Central Tendency--Range: Example 5TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 6 | Math Example--Measures of Central Tendency--Range: Example 6TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 7 | Math Example--Measures of Central Tendency--Range: Example 7TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 8 | Math Example--Measures of Central Tendency--Range: Example 8TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 9 | Math Example--Measures of Central Tendency--Range: Example 9TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of a set of numbers: 22, 13, 15, 1, 16, 28, 3, 5, 18, 42, 8, 9. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 41. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a set of numbers and find their difference. The process encourages critical thinking and helps students visualize the relationship between numbers in a dataset. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 10 | Math Example--Measures of Central Tendency--Range: Example 10TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: -33, 38, 29, -8, 12, 2, 36, -8, 12, 18, -23, 50. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 83. This example is particularly useful as it includes both positive and negative numbers, helping students understand how to handle different types of values when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 11 | Math Example--Measures of Central Tendency--Range: Example 11TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 16, 50, 24, 31, 30, 6, 22, 32, 43, 27, 48, 17, 36. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 44. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 12 | Math Example--Measures of Central Tendency--Range: Example 12TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 13 | Math Example--Measures of Central Tendency--Range: Example 13TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 14 | Math Example--Measures of Central Tendency--Range: Example 14TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 15 | Math Example--Measures of Central Tendency--Range: Example 15TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |
|
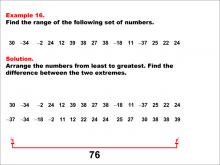
Math Example--Measures of Central Tendency--Range: Example 16 | Math Example--Measures of Central Tendency--Range: Example 16TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |
|
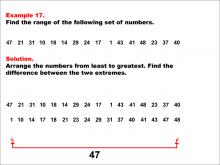
Math Example--Measures of Central Tendency--Range: Example 17 | Math Example--Measures of Central Tendency--Range: Example 17TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 18 | Math Example--Measures of Central Tendency--Range: Example 18TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 19 | Math Example--Measures of Central Tendency--Range: Example 19TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 20 | Math Example--Measures of Central Tendency--Range: Example 20TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |
|
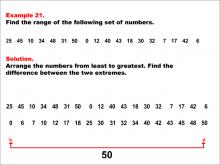
Math Example--Measures of Central Tendency--Range: Example 21 | Math Example--Measures of Central Tendency--Range: Example 21TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
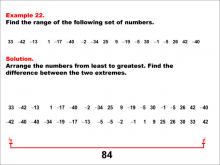
|
Math Example--Measures of Central Tendency--Range: Example 22 | Math Example--Measures of Central Tendency--Range: Example 22TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 23 | Math Example--Measures of Central Tendency--Range: Example 23TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
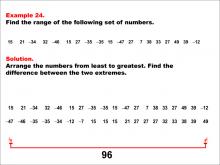
|
Math Example--Measures of Central Tendency--Range: Example 24 | Math Example--Measures of Central Tendency--Range: Example 24TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 25 | Math Example--Measures of Central Tendency--Range: Example 25TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 42, 31, 16, 0, 35, 26, 30, 14, 6, 2, 13, 37, 33, 36, 19, 48, 3, 9, 45, 12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of non-negative numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 26 | Math Example--Measures of Central Tendency--Range: Example 26TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 28, 49, 1, -19, -37, 43, 27, 32, -10, 39, -19, -48, -49, 28, 36, 37, 44, 42, 29, -17. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 98. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
MATH EXAMPLES--The Range | MATH EXAMPLES--The Range
This set of tutorials provides 26 examples of calculating the range. NOTE: The download is a PPT file. |
Data Analysis |