Illustrative Math Alignment: Grade 6 Unit 8

Data Sets and Distributions

Lesson 4: Dot Plots

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
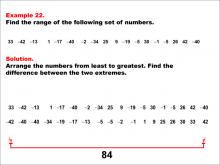
Math Example--Measures of Central Tendency--Range: Example 23	Math Example--Measures of Central Tendency--Range: Example 23 Topic Measures of Central Tendency Description This example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.	Data Analysis
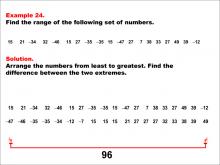
Math Example--Measures of Central Tendency--Range: Example 24	Math Example--Measures of Central Tendency--Range: Example 24 Topic Measures of Central Tendency Description This example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.	Data Analysis
Math Example--Measures of Central Tendency--Range: Example 25	Math Example--Measures of Central Tendency--Range: Example 25 Topic Measures of Central Tendency Description This example demonstrates how to find the range of the following set of numbers: 42, 31, 16, 0, 35, 26, 30, 14, 6, 2, 13, 37, 33, 36, 19, 48, 3, 9, 45, 12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of non-negative numbers and find their difference.	Data Analysis
Math Example--Measures of Central Tendency--Range: Example 26	Math Example--Measures of Central Tendency--Range: Example 26 Topic Measures of Central Tendency Description This example illustrates how to find the range of the following set of numbers: 28, 49, 1, -19, -37, 43, 27, 32, -10, 39, -19, -48, -49, 28, 36, 37, 44, 42, 29, -17. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 98. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 34	Math Example--Measures of Central Tendency--Median: Example 34 Topic Measures of Central Tendency Description This example demonstrates finding the median of the following set of numbers: -4, -44, 24, -48, 35, -3, 50, 34, -32, 42, 11, 22, -49, -4, -31, 41, 30, 17. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of 14.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 33	Math Example--Measures of Central Tendency--Median: Example 33 Topic Measures of Central Tendency Description This example illustrates the process of finding the median for the set of numbers: -22, 30, -39, 46, 50, 27, -42, -15, 15, -14, 47, -31, 21, -2, -27, -9, -22, -9. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of -4.5.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 32	Math Example--Measures of Central Tendency--Median: Example 32 Topic Measures of Central Tendency Description This example demonstrates finding the median of the following set of numbers: 50, 5, 24, 10, 11, 0, 42, 26, 13, 44, 0, 28, 25, 44, 12, 33, 8, 39. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of 24.5.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 38	Math Example--Measures of Central Tendency--Median: Example 38 Topic Measures of Central Tendency Description This example demonstrates finding the median of the following set of numbers: 3, 5, 1, 4, 2. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 3.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 39	Math Example--Measures of Central Tendency--Median: Example 39 Topic Measures of Central Tendency Description This example illustrates the process of finding the median for the set of numbers: 2, 5, 7, 10, 12. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 7.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 40	Math Example--Measures of Central Tendency--Median: Example 40 Topic Measures of Central Tendency Description This example demonstrates the general process of finding the median for a set of numbers. The solution involves arranging the numbers from least to greatest and then identifying the middle value. The procedure differs slightly depending on whether there is an odd or even number of terms in the dataset.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 37	Math Example--Measures of Central Tendency--Median: Example 37 Topic Measures of Central Tendency Description This example illustrates the process of finding the median for the set of numbers: 3, 1, 4, 2, 5. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 3.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 18	Math Example--Measures of Central Tendency--Mode: Example 18 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image illustrates finding the mode of a set. The numbers are sorted and two modes are identified and highlighted. This example demonstrates that a data set can have multiple modes, even when it contains both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 19	Math Example--Measures of Central Tendency--Mode: Example 19 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows a set of numbers with no mode. The numbers are arranged in ascending order to demonstrate that no number repeats. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 20	Math Example--Measures of Central Tendency--Mode: Example 20 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image displays a math example where the mode is found by sorting the numbers and identifying the most frequent one. After arranging the numbers from least to greatest, it becomes clear that 0 appears twice, while all other numbers appear only once, making 0 the mode of this data set.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 21	Math Example--Measures of Central Tendency--Mode: Example 21 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows Example 21, focusing on finding the mode of a set of numbers. The numbers are listed in random order and then sorted from least to greatest. The mode is highlighted in red, demonstrating how to identify the mode when a number appears more frequently than others in a data set.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 22	Math Example--Measures of Central Tendency--Mode: Example 22 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows Example 22, which involves finding the mode of a set of numbers. The numbers are sorted from least to greatest, but no number repeats more than once, indicating no mode. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 23	Math Example--Measures of Central Tendency--Mode: Example 23 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows Example 23 with a set of numbers where the mode is determined by sorting and identifying the most frequent number. The mode is highlighted in red, demonstrating how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 24	Math Example--Measures of Central Tendency--Mode: Example 24 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows Example 24 with a set of numbers where two modes are identified after sorting. Both modes are highlighted in red, demonstrating that a data set can have multiple modes, even when it contains both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 25	Math Example--Measures of Central Tendency--Mode: Example 25 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows a math example focused on finding the mode of a set of numbers. The numbers are arranged in ascending order, and it is highlighted that there is no mode in this data set. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 26	Math Example--Measures of Central Tendency--Mode: Example 26 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image provides a math example on finding the mode of a number set. The numbers are sorted in order with the mode (2) highlighted as it appears most frequently. This demonstrates how to identify the mode when a number appears more frequently than others in a data set.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 31	Math Example--Measures of Central Tendency--Mode: Example 31 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The numbers are listed, and a solution is provided below. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 32	Math Example--Measures of Central Tendency--Mode: Example 32 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The numbers are listed, and a solution is provided below. This example demonstrates how to identify the mode when a number appears more frequently than others in a data set.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 33	Math Example--Measures of Central Tendency--Mode: Example 33 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows an example problem asking to find the mode of a set of numbers. The numbers are listed and then rearranged from least to greatest. The mode is highlighted in red. This example demonstrates that a data set can have multiple modes, even when it contains both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 34	Math Example--Measures of Central Tendency--Mode: Example 34 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image presents a problem where the task is to find the mode of a given set of numbers. The numbers are arranged in order but no number appears more than once; hence there is no mode. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 35	Math Example--Measures of Central Tendency--Mode: Example 35 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image displays a math example where a set of numbers is provided to find the mode. The numbers are sorted and the mode is highlighted in red as it appears multiple times in the list. This example demonstrates how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 36	Math Example--Measures of Central Tendency--Mode: Example 36 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image features an example problem asking for the mode of a list of numbers. After sorting them in ascending order and identifying duplicates with highlights in red indicating multiple modes present in this example. This demonstrates that a data set can have multiple modes, even when it contains both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 37	Math Example--Measures of Central Tendency--Mode: Example 37 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. An example of finding the mode in a set of numbers is presented. The numbers are listed, sorted, and analyzed to determine if there is a mode. The result is "No Mode." This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 38	Math Example--Measures of Central Tendency--Mode: Example 38 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. An example showing how to find the mode in a set of numbers is presented. The numbers are sorted and analyzed to find that "42" is the mode. This demonstrates how to identify the mode when a number appears more frequently than others in a data set.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 39	Math Example--Measures of Central Tendency--Mode: Example 39 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. An example illustrating how to find the mode in a set of numbers is presented. The numbers are sorted and analyzed to reveal two modes: "43" and "44." This demonstrates that a data set can have multiple modes, which occurs when two or more numbers appear with the highest frequency.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 40	Math Example--Measures of Central Tendency--Mode: Example 40 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. An example showing how to find the mode in a set of negative and positive numbers is presented. The analysis shows there is "No Mode." This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 41	Math Example--Measures of Central Tendency--Mode: Example 41 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 41 shows a set of numbers with instructions to find the mode. The numbers are arranged from least to greatest, and the number 27 is highlighted as the mode. This demonstrates how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 42	Math Example--Measures of Central Tendency--Mode: Example 42 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 42 presents a set of numbers with instructions to find the mode. The numbers are sorted from least to greatest, and both 12 and 38 are highlighted as modes. This demonstrates that a data set can have multiple modes, even when it contains both positive and negative numbers.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 43	Math Example--Measures of Central Tendency--Mode: Example 43 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 43 displays a set of numbers with instructions to find the mode. After arranging them from least to greatest, it concludes there is no mode as no number repeats more than once. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 44	Math Example--Measures of Central Tendency--Mode: Example 44 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 44 provides a set of numbers with instructions to find the mode. The numbers are arranged in ascending order and the number 24 is highlighted as the mode. This demonstrates how to identify the mode when a number appears more frequently than others in a data set.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 45	Math Example--Measures of Central Tendency--Mode: Example 45 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows Example 45, which involves finding the mode of a set of numbers. The numbers are listed, and the solution involves sorting them and identifying the mode. This example demonstrates that a data set can have multiple modes, which occurs when two or more numbers appear with the highest frequency.	Data Analysis
Math Example--Measures of Central Tendency--Mode: Example 64	Math Example--Measures of Central Tendency--Mode: Example 64 Topic Measures of Central Tendency Description This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows Example 64 with a list of numbers. After sorting them in ascending order without any repetition in frequency higher than others, it concludes with "No Mode." This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 10	Math Example--Measures of Central Tendency--Median: Example 10 Topic Measures of Central Tendency Description This example demonstrates finding the median of the following set of numbers: 6, -19, 38, 47, 46, -46, 15, 10, 24, 16. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of 15.5.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 11	Math Example--Measures of Central Tendency--Median: Example 11 Topic Measures of Central Tendency Description This example illustrates the process of finding the median for the set of numbers: 50, 41, 30, 30, 47, 31, 45, 12, 6, 14, 39. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 31.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 12	Math Example--Measures of Central Tendency--Median: Example 12 Topic Measures of Central Tendency Description This example demonstrates finding the median of the following set of numbers: -24, 50, -22, -27, 43, 41, 1, 27, -13, 7, 0. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 1.	Data Analysis
Math Example--Measures of Central Tendency--Median: Example 13	Math Example--Measures of Central Tendency--Median: Example 13 Topic Measures of Central Tendency Description This example illustrates the process of finding the median for the set of numbers: 0, 25, 26, 49, 39, 27, 1, 27, 38, 49, 10, 40. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an even number of terms, the median is calculated as the average of the two middle terms, resulting in a median of 27.	Data Analysis

Illustrative Math Alignment: Grade 6 Unit 8

Data Sets and Distributions

Lesson 4: Dot Plots

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic